本节书摘来自异步社区《Python算法教程》一书中的第2章,第2.4节,作者[挪威]Magnus Lie Hetland(赫特兰), 凌杰 译,更多章节内容可以访问云栖社区“异步社区”公众号查看。
2.4 请提防黑盒子
虽然算法工作本身通常都相当抽象,但我们在实现自己的算法时还是要留些心眼。因为在编程时,我们必须依赖一些组件,而这些组件通常都不是我们自己写的,所以依赖于这些“黑盒子”,而不知道其任何内容对我们来说多少是一种风险。在这本书中,您将会看到一系列被标识为“黑盒子”的侧边栏。在这些侧边栏中,我们将会简略讨论Python某些部分中的各种可用的算法。这里既有语言内置的,也有属于标准库的。我们会将它们都包括进来,因为这些算法是非常有意义的,它们能告诉我们Python的一些工作方式,并且让我们见识到一些更为基本的算法。
然而,我们会遇到的问题也并不只有黑盒子而已。事情没有那么简单。如果不够仔细的话,Python与机器本身所用的很多机制都会成为我们的绊脚石。在一般情况下,我们的程序越重要,就越不应该相信黑盒子这样的东西,并且要试图找出其背后究竟隐藏了什么。在接下来的两节内容中,将揭示两个需要我们特别提防的陷阱。趁您的注意力还尚未离开本节,请先记住以下内容。
- 当性能成为重点问题时,要着重于实际分析而不是直觉。我们的确可能会有一些隐藏的性能瓶颈,但它们很可能并不在您所认为的地方。
- 当正确性至关重要时,最好的做法是用不同的实现体来对答案进行多次计算(并且最好交由不同的程序员来编写)。
后者是当今许多性能关键(performance-critical)系统中所使用的冗余原则,也是Foreman S. Acton在他的《Real Computing Made Real》一书中提出的关键建议之一,其有助于我们提防一些科学及工程软件当中的计算错误。当然,我们还需要根据每种具体情况来权衡其正确性和性能之间的成本值(例如,正如我们之前所说,如果程序已经够快了,就不必再去优化它了)。
在接下来的这两节内容中,我们要处理两个截然不同的话题。第一个话题与被隐藏的性能陷阱有关,即相关操作看起来似乎已经足够好了,但却可能会由一个线性级操作变成一个平方级操作。第二个话题在算法书中不常被讨论,但重要性非常值得注意,即存在于各种浮点运算当中的许多陷阱。
2.4.1 隐性平方级操作
首先来看看下面两种查询列表元素的方式:

这两种方式都很快,而且似乎在list之上再构建一个set是件毫无意义的事——根本就是多余的工作,对吧?好吧,这得取决于具体情况。如果我们打算进行多次成员查询操作的话,这样做或许是值得的,因为成员查询在list中是线性级的,而在set中则是常数级的。再比如,如果您想依次往某个集合里添加新值,并在每一步中都检查该值是否已被添加的话,应该怎么做呢?这种情况我们在整本书中将会多次遇到。这件事用list来处理的话,运行时间是平方级的,而改用set就可以获得线性级时间。这是一个巨大的差距。这条经验显示了在工作中正确利用内置数据结构的重要性。
同样,这条经验也适用于我们之前所讨论的关于使用双向队列(deque)优于在某个list首端插入对象的那个例子。但也有一些不那么明显的例子,它们也会带来许多问题。例如,下面我们用一种“明显”的方式从数据源提供的片段逐步构建一个字符串:

如您所见,这段代码完全没有问题。而且事实上,由于Python自身采用了一些非常聪明的优化,它在扩展到某一规模之前一直都能工作得很好——但随后这些优化的作用就会消退,我们的运行时间也因此猛然呈现出平方级的增长。其问题在于,(在排除优化因素的情况下)我们需要在每次执行+=操作时新建一个字符串,并复制上一个字符串内容。至于排序问题为什么是平方级时间,我们会在下一章中详细讨论,但现在我们只需要明白这是一个有风险的业务逻辑就行了。并且,它有一个更好的解决方案:

甚至您还可以再简化一下:
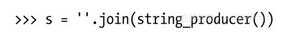
基于相同的理由,该版本也可以改善我们之前那个append例子的效率。append操作允许我们将原有空间加上一定的百分比来进行“过度”分配,其可用空间的增长方式是指数式的,这时,append操作的成本在交由所有操作平均承担(均摊)的情况下就成了常数级操作。
我们还可能遇到某种处理速度是平方级时间,但比上面的例子隐藏得更深的情况。我们来看看下面这个方案:

Python环境会报错,并要求我们改用' '.join()(这是对的)。但如果我们改用list又会如何呢?
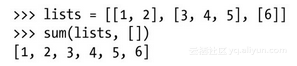
这段代码也没有问题,并且看起来还很优雅,但其实不然。显然在幕后,sum函数对我们要叠加的东西一无所知,何况还要一次又一次地重复执行这样的加法操作。因此这种方法与之前的字符串+=那个例子一样,都是平方级的运行时间。下面是一个更好的选择:

只要测试一下这两个版本的运行时间,就会发现当list的长度很短时,它们之间就没有多少差距,但一旦超出某个长度,前面的sum版本就会彻底完败。
2.4.2 浮点运算的麻烦
仅通过有限的长度,我们无法完全精确地表达绝大多数实数的值。浮点数这种重大发明似乎让它们的表示显得很精确,然而,即便它给我们带来巨大的计算能力,但同时也会使我们更容易摔跟斗。很大程度上,正如Knuth在《The Art of Computer Programming 》第二卷中所说的,“浮点计算天然就是不精确的,并且程序员很容易滥用它们,以至于我们的计算结果最终基本上是由一堆‘噪声’组成的。”
Python非常善于对您隐藏这些问题。如果我们希望寻求某种安慰感的话,这倒是一件好事,但同时它也就无法帮助我们了解实际所发生的事情。例如,在当前版本的Python中,我们会看到下面这种很合理的行为现象:

这看上去当然像是数字0.1的精确表示。除非您对此有更好的了解,否则一旦您了解到它不是这样的,这很可能会让您感到吃惊。下面我们来试试Python的早期版本(例如2.6),这会让这里的黑盒子更透明一点:

现在我们得到了一些进展,下面我们再更进一步(在这里,您可以自由选择是否使用最新版的Python):

嗨!如果没有之前的浮点数知识的话,我们肯定不会想到是这种结果吧?
事情是这样的,整数在任何进位制的系统中都可以有精确表示法,它可以是二进制的、十进制的或者其他某种形式。但到了实数这里就有些复杂了。Python的官方教程用了专门一节内容对此做了非常好的说明2,并且David Goldberg也为此写了一篇非常优秀(且全面)的教学论文。其基本思想很简单,即如果我们将1/3这个数字表示成十进制数的话,那么想要做到精确显然是不可能的,对吗?但如果我们用的是一个三元数字系统的话(基数为3),那么我们就能很容易地将其表示成0.1。
我们的第一课就是“不要对浮点数进行等值比较”。因为通常情况下,这样做是毫无意义的。但尽管如此,我们还是会希望在许多应用(如几何运算)中进行这样的比较。其实我们可以换一种思路,我们可以检查它们是否接近于相等。例如,我们可以采用与unittest模块中的assertAlmostEqual方法类似的思路来做到这点:

除此之外,如果我们需要某种精确的十进制浮点数表示法,还可以选择使用其他工具,如decimal模块:

如果我们需要对一定数位范围内的十进制数进行精确计算的话(例如处理某些财务数据),该模块就必不可少了。此外,在某些特定数学以及科学应用中,我们还可能会需要用到一些其他工具,如Sage模块:3
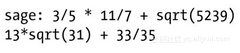
正如您所见,Sage使用的是数学上的语义符号,因此我们可以从中获取更精确的答案(尽管在需要时,我们也可以用它来获取相应的十进制近似值)。尽管如此,这类数学符号(或decimal模块)在真正使用中的运行效率也远远不如那些内置在硬件中的浮点运算功能。
如果我们发现在自己所做的浮点运算中,精度是关键问题的话(也就是说,我们要做的不只有排序这一类事情),那么稍早前提到的Acton的书是一个很好的参考源。下面我们简单回顾一下他所举的那个例子:如果我们将两个接近等值的子表达式相减,通常会丢失大量的有效数字。因此,想要达到更高的精度,我们就得重写相关的表达式。下面我们来看一个具体的表达式sqrt(x+1)-sqrt(x)(我们假设这里的x是一个非常大的数),我们要做的是尽可能排除减法运算所带来的风险。通过将表达式sqrt(x+1)+sqrt(x)与乘法及除法运算的搭配使用,我们最终得到了一个与原表达式等效的数学式:1.0/ sqrt(x+1)-sqrt(x),但同时我们去掉了里面的减法运算。下面我们来对比一下这两个版本:

如您所见,尽管这两个表达式在数学上是等效的,却各自给出了不同的答案(显然后者的精度更高一些)。
