本节书摘来自华章出版社《 线性代数及其应用 （原书第4版）》一书中的第2章，第2.1节，作者:（美）戴维C. 雷（David C. Lay）马里兰大学帕克学院 著刘深泉 张万芹 陈玉珍 包乐娥 陆 博 译，更多章节内容可以访问云栖社区“华章计算机”公众号查看
第2章 矩 阵 代 数
介绍性实例 飞机设计中的计算机模型
为了设计下一代的商业和军用飞机，波音的幻影工作室的工程师们使用三维建模和计算流体动力学. 他们在建造实际的模型之前，研究一个虚拟的模型周围的空气流动，这样做可以很大程度地缩短设计周期，降低成本，而线性代数在这个过程中起了关键的作用.
虚拟的飞机模型的设计从数学的线形轮廓模型开始，它存储在计算机内存中，并可显示在图形显示终端. （图示给出波音777的模型.）这个数学模型组织和影响设计和制造飞机外部和内部的每一个过程. 计算流体动力学分析主要考虑的是飞机外部表层的设计.
虽然飞机精巧的外表看上去是光滑的，但其表面的几何曲面是十分复杂的. 除了机翼和机身，飞机上还有引擎机舱、水平尾翼、狭板、襟翼、副翼. 空气在这些结构上的流动决定了飞机在天空中如何运动. 描述气流的方程很复杂，它们必须考虑到引擎的吸气量、引擎的排气量和机翼留下的尾迹. 为了研究气流，工程师们需要飞机表面的精确描述.
用计算机建立飞机外表的模型，首先在原来的线形轮廓模型上添加三维的立方体格子. 这些立方体有的处于飞机的内部，有的在外部，有的和飞机的表面相交. 计算机选出这些相交的立方体，并进一步细分，保留仍然和飞机表面相交的立方体. 这种细分过程一直进行下去，直到立方体非常精细. 一个典型的网格可以含有超过400 000个的立方体.
研究飞机表面的气流的过程包含反复求解大型的线性方程组Ax=b ，涉及的方程和变量个数达到2百万个. 向量 b随来自网格的数据和前面的方程的解而改变. 利用现在商业上买得到的最快的计算机，幻影工作组求解一个气流问题要用数小时至数天的时间. 工作组分析方程组的解之后，会对飞机的外表进行稍微的修改，整个过程又再重新开始，计算流体动力学的分析有可能要进行数千遍.
本章给出协助求解这样大规模方程组的两个重要的概念：
. 分块矩阵：一个典型的计算流体动力学的方程组会有“稀疏”的系数矩阵，上面有许多零元素. 将变量正确地分组会产生有许多零方块的分块矩阵. 2.4节介绍了这种矩阵及其应用.
. 矩阵分解：即使使用分块矩阵，这样的方程组还是相当的复杂. 为了进一步简化计算，波音的计算流体动力学软件使用了对系数矩阵进行LU分解的方法. 2.5节将讨论LU和其他有用的矩阵分解. 关于分解的更详细的内容在本书后面出现.
为了分析气流问题的解，工程师们希望将飞机表面的气流显示出来. 他们利用计算机图形以及线性代数作为图形的引擎. 飞机外表的线形轮廓模型作为许多矩阵数据存储. 图像在计算机屏幕上染色显示后，工程师们可以改变图像的大小，对局部区域进行缩放，以及对图像旋转以看到在视图中被隐藏的部位. 这里的每个操作是通过适当的矩阵乘法运算来实现的. 2.7节解释了其中的基本思想.图2-1为波音公司为机翼做设计.
当我们学会矩阵的代数运算后，我们分析和解方程的能力将会大大提高. 本章中的定义和定理给出一些基本的工具来处理涉及两个或更多个矩阵的线性代数问题. 对方阵而言，2.3节的逆矩阵定理把许多以前学过的概念联系在一起. 2.4节与2.5节研究分块矩阵以及矩阵的分解，它们在线性代数的应用很广. 2.6节和2.7节给出了矩阵代数在经济学、计算机图形学中的两个有趣应用.
2.1 矩阵运算
若A是 m*n矩阵，即有m 行n 列的矩阵，A的第i 行第j 列的元素用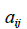 
表示，称为A的 (i,j)元素，见图2-2. 例如，（3,2）元素是在第3行第2列的数
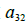，A的各列是 
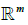的向量用（黑体字母） 
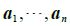表示. 当我们特别注意A的各列时，我们写成 
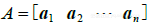，注意 
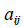是第 j个列向量
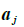（从上面算起）的第i 个元素.
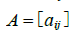的对角线元素是 
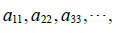它们组成A的主对角线. 对角矩阵是一个方阵，它的非对角线元素全是0. 元素全是零的 m*n矩阵称为零矩阵，用0表示. 0的维数通常可由上下文知道，否则我们就用
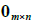表示.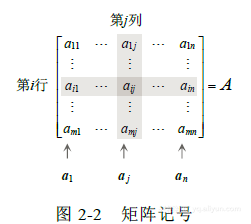
和与标量乘法
前面叙述过的向量运算可以自然地推广到矩阵. 我们称两个矩阵相等，若它们有相同的维数（即有相同行数和列数），而且对应元素相等. 若A与B都是 mn矩阵，则和 A+B也是 mn矩阵. 它的各列是A与B对应列之和，因列的向量加法是对应元素相加，A+B 的每个元素也就是A与B的对应元素相加. 仅当A与B有相同维数，A+B 才有定义.
例1 设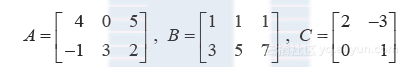
则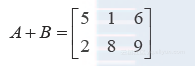 
但 A+C没有定义，因A与C的维数不同. ?
若r是标量而A是矩阵，则标量乘法 rA是一个矩阵，它的每一列是A的对应列的r倍. 与向量相同，定义-A 为(-1)A 而A-b 为 A+(-1)B.
例2 设A与B如例1，则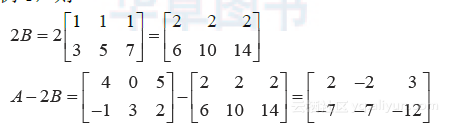
在例2中，计算 A-2B时，不必化为 A+(-1)2b，因为通常的代数法则对矩阵的和与标量乘法仍适用，如下列定理所示.
定理1 设 A,B,C是相同维数的矩阵，r与s为数，则有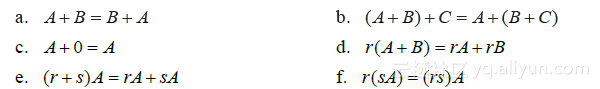
为证明定理1的各个等式，只要证明左端矩阵和右端矩阵有相同维数且对应各列相等. 维数是无问题的，因 A,B,C的维数相同. 而由向量的类似性质，立即知道两端的对应各列相等. 例如，若A,B,C 的第j列分别是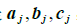 
，则(A+B)+C与A+(B+C) 的第j列分别是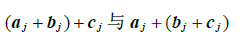
因对每个j，这两个向量相等，这就证明了（b）.
由于加法的结合律，我们只要写A+B+C 即可，它无论按(A+B) +C或A+(B+C) 计算都得同一结果. 同样对四个或更多矩阵也可定义加法.
矩阵乘法
当把矩阵B乘以向量 x，它将x 变换为向量 Bx，若这向量又乘以矩阵A，结果得向量 A(B)x，见图2-3.
于是 A(Bx)是由 x经复合映射变换所得，此映射是1.7节所研究的线性变换. 我们的目的是将此复合映射表示为乘以一个矩阵的变换，此矩阵记为AB，即
（1）
见图2-4.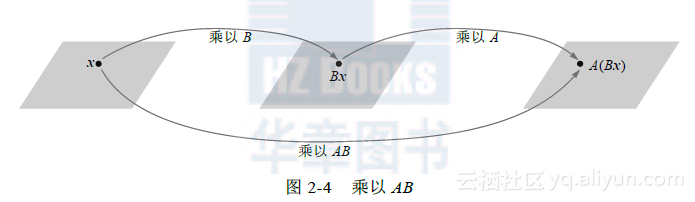
若A是mn 矩阵，B是 np矩阵，x属于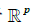 
，用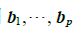 
表示B的各列，而 x的元素为
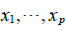，则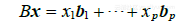
由于乘以A 的线性性质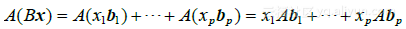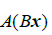
向量
是向量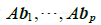 
的线性组合，以x 的元素为权，若我们把这些向量表示成一个矩阵的各列，就有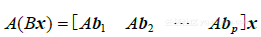
于是乘以矩阵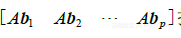
把x 变为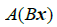 
，我们已经找到了所需要的矩阵.
定义 若A是 mn矩阵，B是 np矩阵，B的列是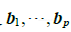
，则乘积AB是 m*p矩阵，它的各列是 
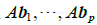，即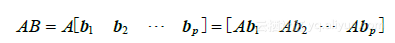
这个定义使（1）式对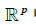 
中所有 x成立，方程（1）证明图2-4中的复合映射是线性变换，它的标准矩阵是AB，矩阵乘法对应线性变换的复合.
例3 计算AB，其中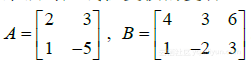
.
解 写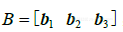
，计算
注意，由AB的定义，它的第一列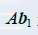 
是A的各列用 
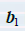的各元素为权的线性组合. 其他各列也是这样.
AB的每一列都是A的各列的线性组合，以B的对应列的元素为权.
显然，A的列数必须等于B的行数，才能使线性组合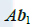
有定义，由定义知，AB的行数等于 的行数，列数等于B的列数.
例4 若A是35矩阵，B是52矩阵，AB和BA是否有定义？若有定义，是什么矩阵？
解 因A有5列，B有5行，乘积AB有定义且是3*2矩阵：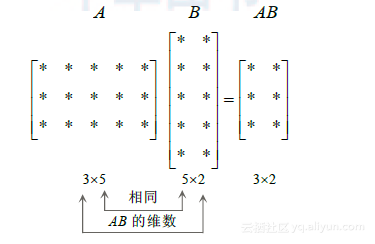
乘积BA没有定义，因B为2列， 有3行. ?
AB的定义对理论与应用是重要的，但下列法则给出了更有效的计算AB的各元素的方法.
计算AB的行列法则
若乘积AB有定义，AB的第i 行第 j列的元素是A的第 i行与B的第 j列对应元素乘积之
和. 若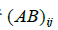 
表示AB的(i,j) 元素，A为 m*n矩阵，则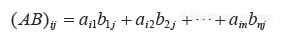
为证明这一法则，设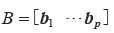 
，AB 的第j 列是
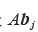，我们可用1.4节的计算 Ax的规则计算 
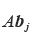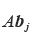. 的第 i个元素是A的第i 行与向量
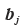的对应元素之积，恰好是上述规则中计算AB的 (i,j)元素的方法.
例5 使用行列法则计算例3中矩阵AB的两个元素，观察其中涉及的数会使你更好地理解计算AB的两种方法结果相同.
解 要找出AB的第1行第3列的元素，考虑A的第1行和B的第3列，把对应元素相乘再加起来，如下所示：
对第2行第2列的元素，用 的第2行和B的第2列：
 例6 求AB的第2行，其中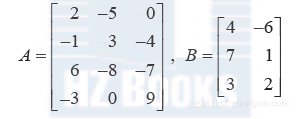
解 由行列法则，AB的第2行是由A的第2行和B的各列相乘所得
注意，由例6可知，计算AB的第2行时，我们仅需把A的第2行写在B的左边，得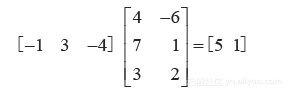
这在一般情况下也是正确的，可由计算AB的行列法则得出. 记row 表示矩阵A的第 i行，则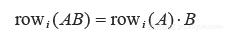
（1）矩阵乘法的性质
下列定理列出了矩阵乘法的重要性质，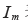 
表示m*m 单位矩阵，对 
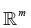中的一切 x，
.
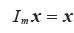定理2 设 为A 矩阵m*n，B.C 的维数使下列各式的乘积有定义.
证 性质（b）~（e）在习题中证明，性质（a）是由于矩阵乘法对应于线性变换的复合，而映射的复合是可结合的. 这里给出（a）的另一个基于矩阵乘积的“列”定义的证明. 设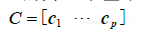
由矩阵乘法的定义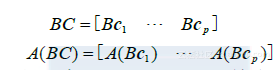
由（1）知，AB 的定义使得对一切 x有A(Bx)=(AB)x ，所以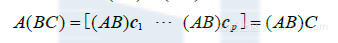
定理1和定理2中的结合律和分配律说明，基本上矩阵表达式中的括号可像实数运算中那样插入和解开，特别地，我们可写乘积 ABC，不管按A(BC) 或(AB)C 计算都相同. 类似地，四个矩阵ABCD 的乘积可按 A(BCD)，(ABC)D或 A(BC)D计算，等等. 计算乘积时不管怎样结合都行，但左右顺序必须保持不变.
乘积中的左右顺序是重要的，因为一般来说 AB与BA 并不相同. 这并不奇怪，因AB的列是A的各列的线性组合，而BA的各列是B的各列的线性组合. 乘积AB的因子的位置需要这样强调，即A被B右乘，或B被A左乘. 若 ，我们称A和B彼此可交换.
例7 设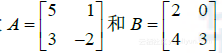 
，证明它们不可交换，即证明
.
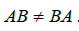解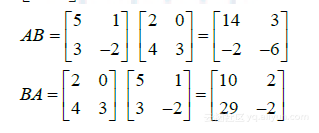 
乘法一般不可交换是矩阵代数与普通实数代数的重要差别，具体例子参阅习题9~12.
警告
- 一般情况下，
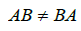. - 消去律对矩阵乘法不成立，即若AB=AC ，一般情况下，B=C 并不成立.（见习题10.）
- 若乘积AB是零矩阵，一般情况下，不能断定A=0 或 B=0.（见习题12.）
矩阵的乘幂
若A是 n*n矩阵，k 是正整数，则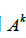 
表示k 个A的乘积.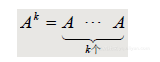
若A不是零矩阵，且x 属于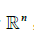
，则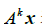
表示 x被A连续左乘 k次. 若k=0 ，则 
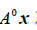就是 x本身. 因此
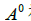被解释为单位矩阵. 矩阵乘幂在理论和应用中都很有用处（见2.6节、4.9节及本书后面的内容）.
矩阵的转置
给定mn 矩阵A，则A的转置是一个nm 矩阵，用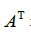
表示，它的列是由A的对应行构成的.
例8 设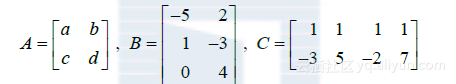
则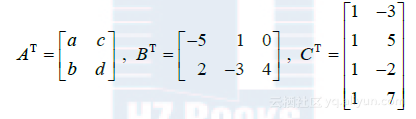
定理3 设A与B表示矩阵，其维数使下列和与积有定义，则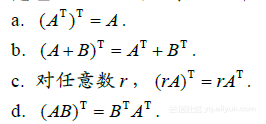
（a）~（c）的证明是直接的，这里省略. （d）的证明见习题33. 通常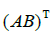 
不等于
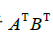，即使乘积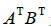
是有定义的. 定理3（d）可推广到多于两个矩阵的乘积，叙述如下：
若干个矩阵的乘积的转置等于它们的转置的乘积，但相乘的顺序相反.
习题中包括说明这些性质的例子.
数值计算的注解
- 在计算机上求出AB的最快方法依赖于计算机存储矩阵的方法. 标准的高性能算法（如LAPACK）中按列计算AB，正如我们所定义的那样.（一个用C++语言写成的LAPACK版本是按行计算AB）.
- AB的定义使我们可在计算机上用并行算法计算，B的列可单独或分组分配给不同的处理器，因此可以同时计算AB的各列.
练习题 - 因
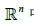中向量可以看作 n*1矩阵，转置矩阵的性质也适用于向量，令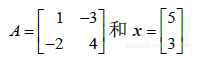
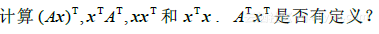
- 设 A为4*4向量， x是
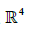中向量. 计算 
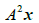的最快方法是什么？计算乘法的次数.
习题2.1
