Classes 2 深度学习
1 深度学习实践
1.1 训练集、验证集、测试集(Train / Dev / Test sets)
对训练执行算法,通过验证集或简单交叉验证集选择最好的模型。
在机器学习发展的小数据量时代,常见做法是将所有数据三七分,就是人们常说的 70%验证集,30%测试集,如果没有明确设置验证集,也可以按照 60%训练,20%验证和 20%测试集来划分。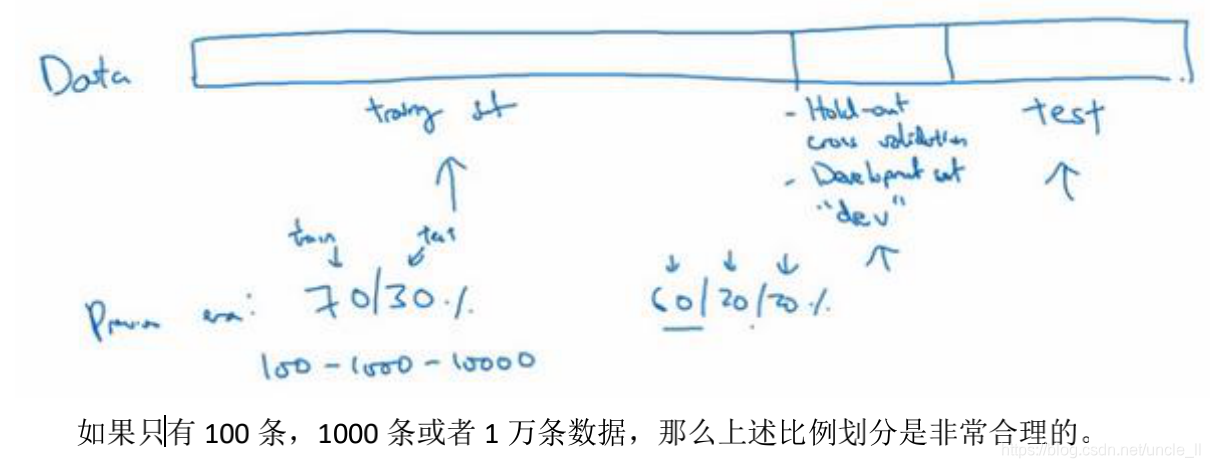
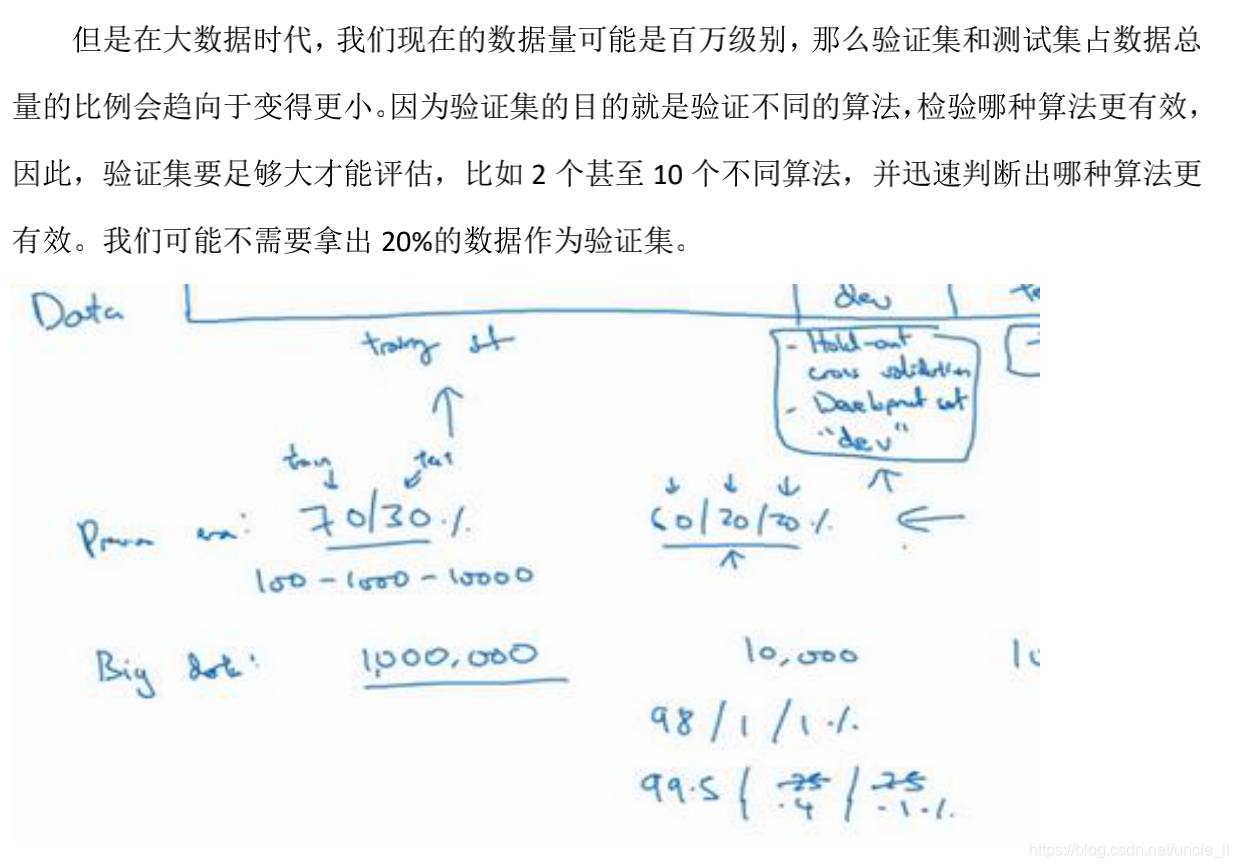
- 假设我们有 100 万条数据,其中 1 万条作为验证集,1 万条作为测试集,100 万里取 1 万,比例是 1%,即:训练集占 98%,验证集和测试集各占 1%。对于数据量过百万的应用,训练集可以占到 99.5%,验证和测试集各占 0.25%,或者验证集占 0.4%,测试集占 0.1%
- 通常将样本分成训练集,验证集和测试集三部分,数据集规模相对较小,适用传统的划分比例,数据集规模较大的,验证集和测试集要小于数据总量的 20%或 10%
- 要确保验证集和测试集的数据来自同一分布
1.2 偏差与方差
- 欠拟合:高偏差 high bias
- 过拟合:高方差 high variance
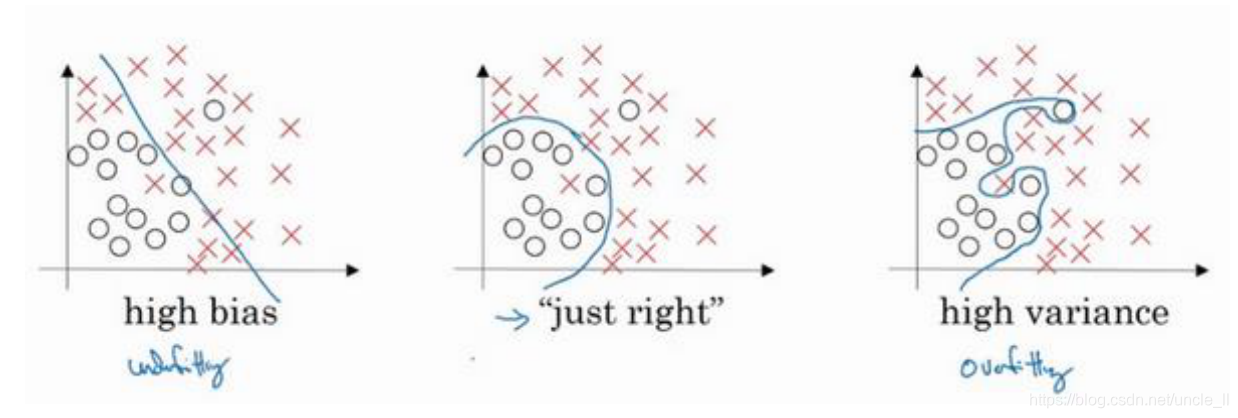

1.3 机器学习基础
- 高偏差解决方法:欠拟合,增大网络模型、更多的时间训练、更好的优化方法
- 高方差解决方法:过拟合,增加训练数据、减小网络模型、加入正则化
1.4 正则化
深度学习可能存在过拟合问题——高方差,有两个解决方法,一个是正则化,另一个是准备更多的数据。但准备更多的数据比较耗时耗力。
以逻辑回归损失函数为例: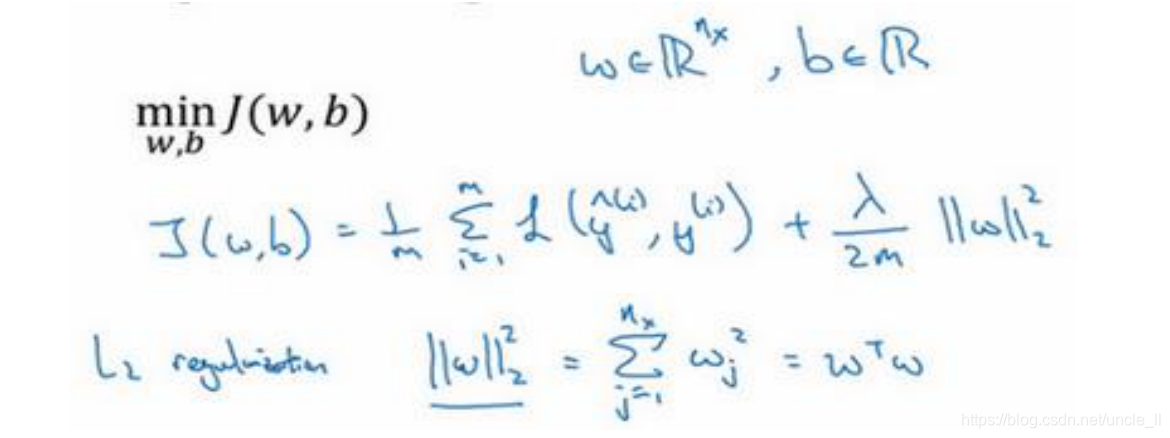
- L0正则:参数为零的个数,难求解
- L1正则:各个参数绝对值之和,侧重于让其为0(LASSO)
- L2正则: 各个参数的平方的和的开方值,侧重于让参数稀疏化(Ridge)
实现参数的稀疏有什么好处吗?
- 可以简化模型,避免过拟合。因为一个模型中真正重要的参数可能并不多,如果考虑所有的参数起作用,那么可以对训练数据可以预测的很好,但是对测试数据就不行了
- 参数变少可以使整个模型获得更好的可解释性
参数值越小代表模型越简单吗?
- 是的。为什么参数越小,说明模型越简单呢,这是因为越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。
总结
- L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已
- 在所有特征中只有少数特征起重要作用的情况下,选择Lasso L1比较合适,因为它能自动选择特征。而如果所有特征中,大部分特征都能起作用,而且起的作用很平均,那么使用Ridge L2也许更合适
- 一般倾向于选择L2正则
𝜆是正则化参数,通常使用验证集或交叉验证集来配置这个参数,尝试各种各样的数据,寻找最好的参数,要考虑训练集之间的权衡,把参数设置为较小值,这样可以避免过拟合
如果正则化参数𝜆变得很大,参数𝑊很小,𝑧也会相对变小,此时忽略𝑏的影响,𝑧会相对变小,实际上,𝑧的取值范围很小,曲线函数𝑡𝑎𝑛ℎ会相对呈线性,整个神经网络会计算离线性函数近的值,这个线性函数非常简单,并不是一个极复杂的高度非线性函数,不会发生过拟合。
1.5 dropout正则化
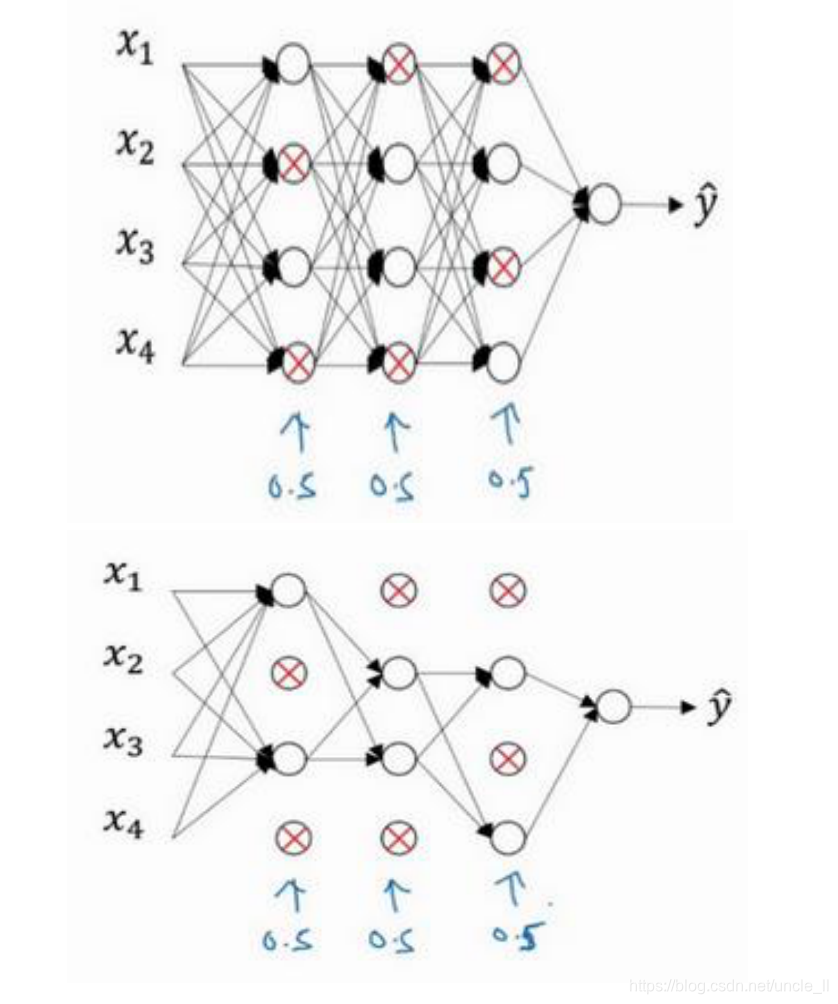
实现方式:反向随机失活(inverted dropout)
在测试阶段,当我们评估一个神经网络时,也就是用绿线框标注的反向随机失活方法,使测试阶段变得更容易
反向随机失活(inverted dropout)方法通过除以 keep-prob,确保激活值a的期望值不变。
在测试阶段,并未使用 dropout,自然也就不用抛硬币来决定失活概率,以及要消除哪些隐藏单元,因为在测试阶段进行预测时,不期望输出结果是随机的。
dropout好处:
- 不要依赖于任何一个特征,因为该单元的输入可能随时被清除, 将产生收缩权重的平方范数的效果。将产生收缩权重的平方范数的效果。
- 每个单元,它不能依靠任何特征,因为特征都有可能被随机清除,或者说该单元的输入也都可能被随机清除,将产生收缩权重的平方范数的效果。
dropout缺点:
- 代价函数𝐽不再被明确定义
使用经验:
- dropout 是一种正则化方法,它有助于预防过拟合。
- 因此除非算法过拟合,不然是不会使用 dropout 的,所以它在其它领域应用得比较少,主要存在于计算机视觉领域
只有存在过拟合时,才决定是否使用dropout。如果不存在过拟合,使用它并不一定能够提升模型性能。
1.6 其它正则化方法
1.数据扩增(data augmentation)
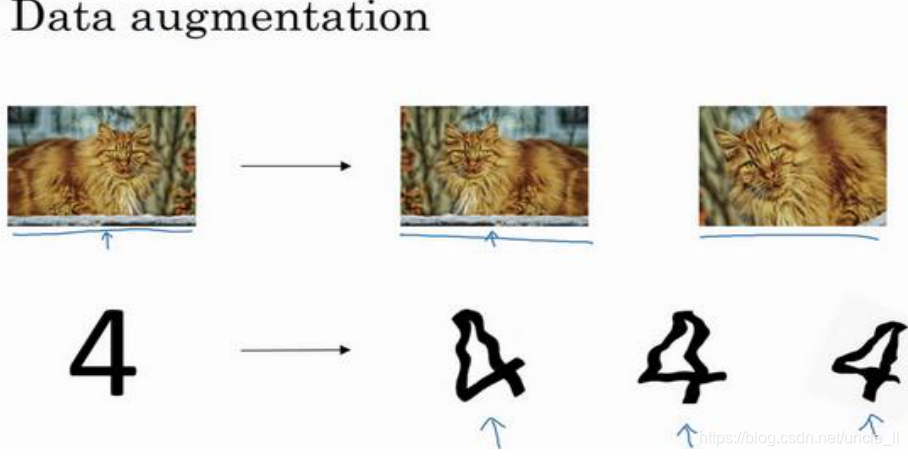
方法:水平垂直翻转、随机裁剪、随机放大裁剪、轻微形变
2.early stopping
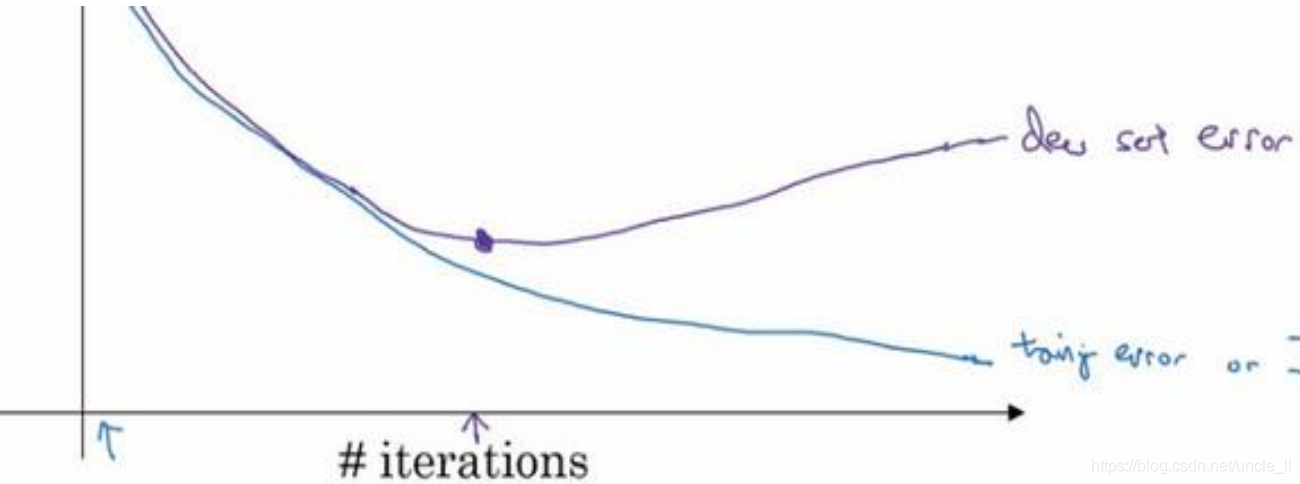
验证集性能有多少次迭代都没有变化时,使用early stop,在此时停止。
优点:
- 只运行一次梯度下降,可以找出𝑤的较小值,中间值和较大
值,而无需尝试𝐿2正则化超级参数𝜆的很多值
缺点:
- 不能独立地处理这两个问题,因为提早停止梯度下降,也就是停止了优化代价函数𝐽,因为现在你不再尝试降低代价函数𝐽,所以代价函数𝐽的值可能不够小。
建议还是使用L2正则化来代替early stopping。
1.7 归一化输入
标准化
标准化需要两个步骤:
- 零均值
- 归一化方差
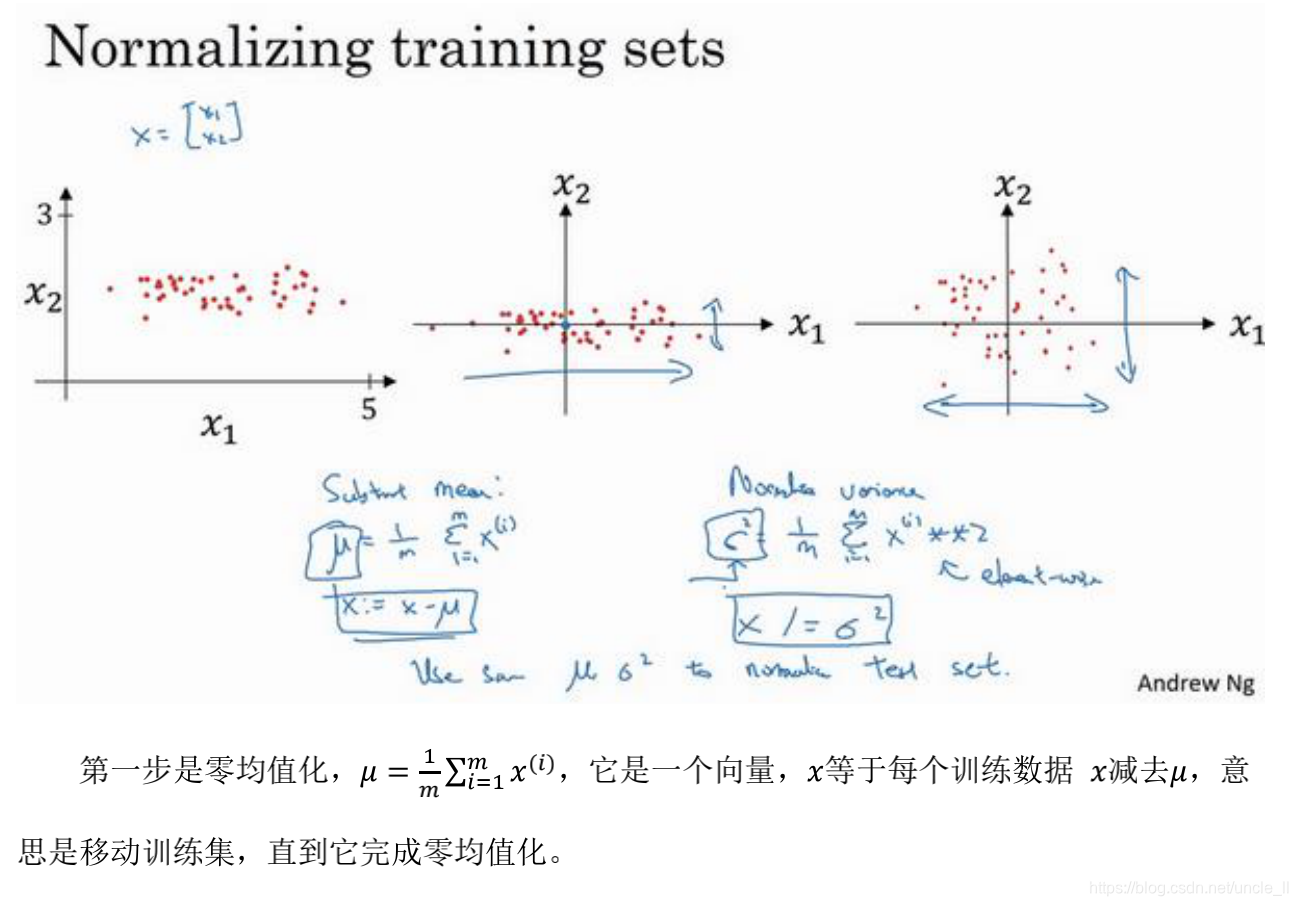
确保所有特征都在相似范围内,通常可以帮助学习算法运行得更快。
1.8 梯度消失/爆炸
训练神经网络,尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸,导数或坡度有时会变得非常大,或者非常小,甚至于以指数方式变小,这加大了训练的难度。
1.9 神经网络的权重初始化

- 随机高斯 初始化变量,然后除以每层节点数的平方根
- 设置的权重矩阵既不会增长过快,也不会太快下降到 0,从而训练出一个权重或梯度不会增长或消失过快的深度网络,也可以加快收敛速度。
2 优化方法
2.1 mini-batch gradient descent

batch: 每次都拿全部的样本进行梯度更新来训练网络,导致速度很慢。
mini-batch: 把训练集分割为小一点的子集,然后用子集进行训练。
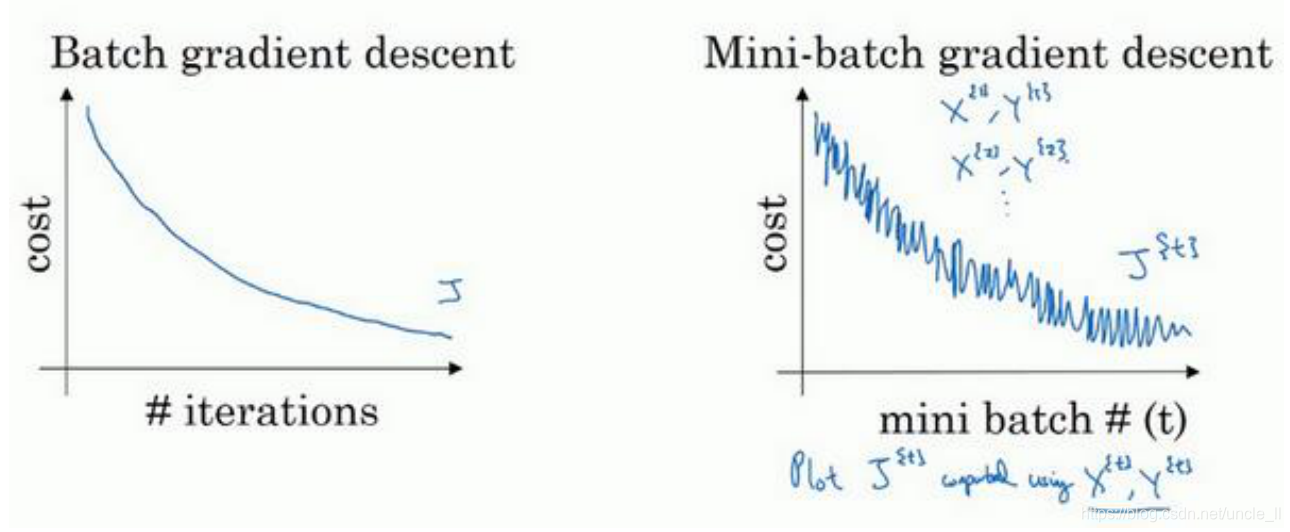
- batch: 训练耗时,曲线更平滑
- mini-batch: 训练更快,曲线有噪声,增大mini-batch数,曲线会平滑些

mini-batch = m ----> batch
mini-batch = 1 ----> sgd
2.2 指数加权平均数

做偏差修正,可以让平均数运算更加准确。初始时候预测结果不准确,导致前期结果有一段不准确。使用偏差修正能够解决这类问题。
2.3 动量梯度下降算法 Momentum
计算梯度的指数加权平均数,并利用该梯度更新权重。比一般的梯度下降算法要快。
等高线纵轴方向波动小些,横轴方向移动快些。
2.4 RMSprop
root mean square prop
减缓𝑏方向的学习,即纵轴方向,同时加快,至少不是减缓横轴方向的学习。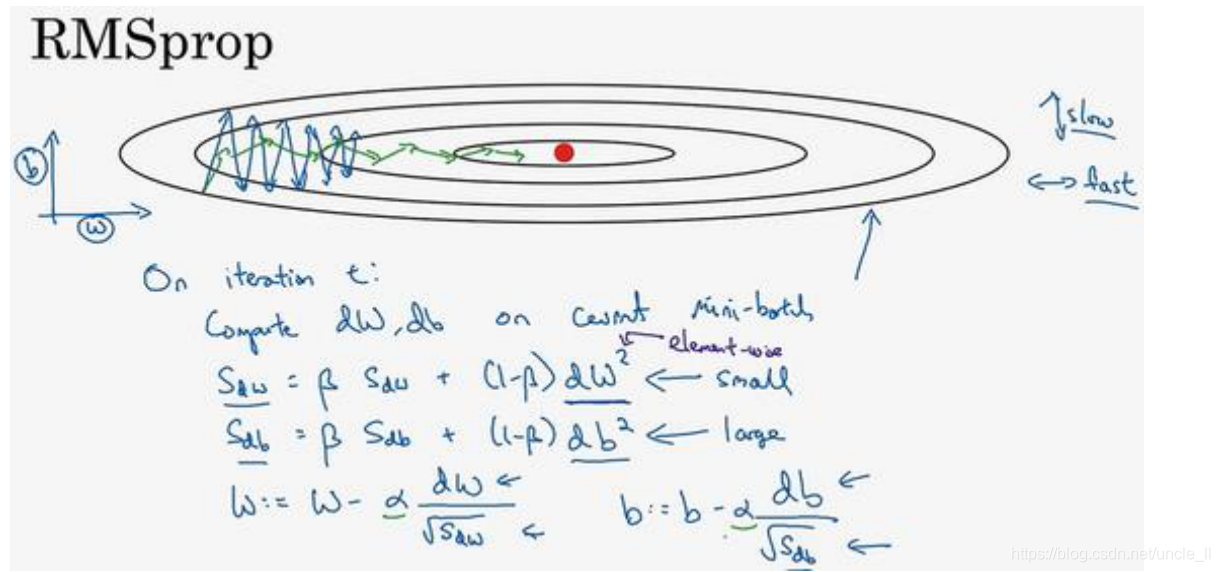
与动量梯度下降有些相似,但是偏导数的平方项,且在进行参数更新的时候,除以开方数。
在横轴方向或者在例子中的𝑊方向,我们希望学习速度快,而在垂直方向,也就是例子中的𝑏方向,希望减缓纵轴上的摆动,所以有了𝑆𝑑𝑊和𝑆𝑑𝑏,我们希望𝑆𝑑𝑊会相对较小,所以我们要除以一个较小的数,而希望𝑆𝑑𝑏又较大,所以要除以较大的数字,这样就可以减缓纵轴上的变化。
2.5 Adam优化算法
Adam 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起。
2.6 学习率衰减
加快学习算法的一个办法就是随时间慢慢减少学习率,将之称为学习率衰减。
减少𝑎的本质在于,在学习初期,能承受较大的步伐,但当开始收敛的时候,小一些的学习率能步伐小一些
3 超参数调试
3.1 参数选择
- 区域网格搜索
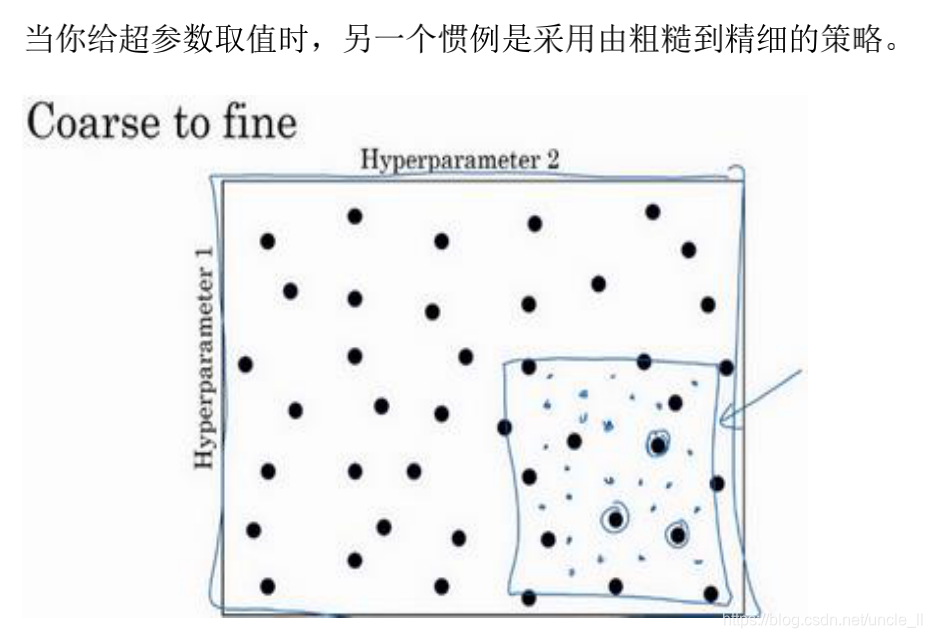
- 尺度范围搜索
用对数标尺搜索超参数的方式会更合理,因此这里不使用线性轴,分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点。
3.2 超参数调试实践
- 熊猫方式:每次只训练一个或几个模型,然后参数优化
- 鱼籽方式:每次训练多个模型,每个模型参数不同
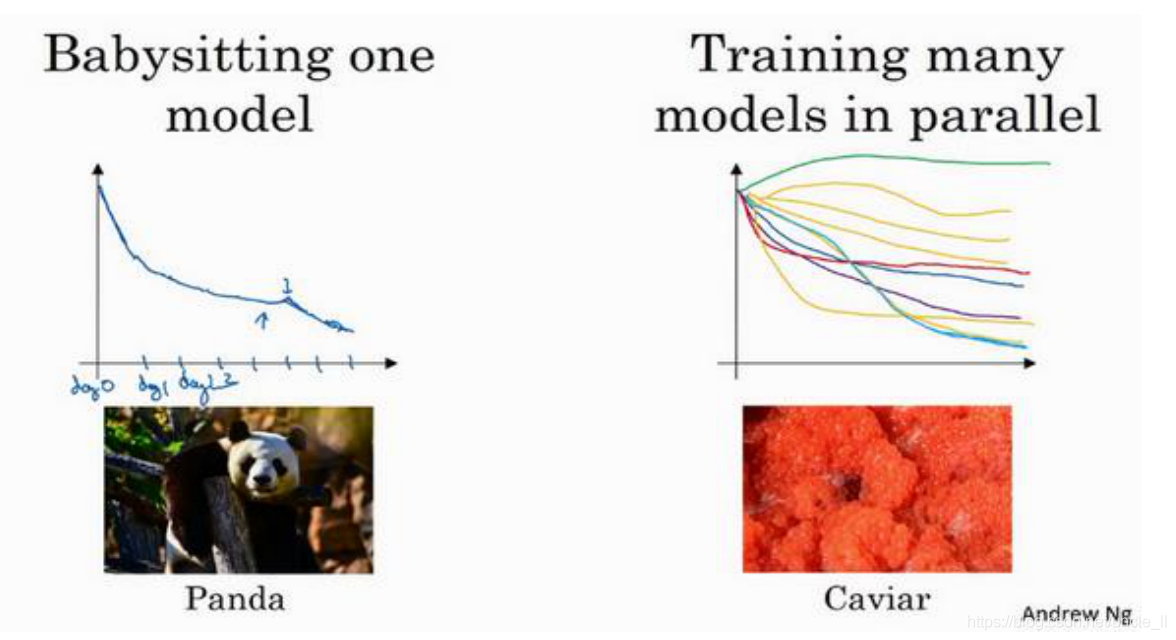
这两种方式的选择,是由你拥有的计算资源决定的,如果你拥有足够的计算机去平行试验许多模型,那绝对采用鱼子酱方式,尝试许多不同的超参数,看效果怎么样
3.3 batch normal
Batch归一化会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会是你的训练更加容易
- 加快学习速度: 类似于逻辑回归输入归一化
- 隐藏层:以就会影响𝑤, 𝑏的训练。简单来说,这就是 Batch 归一化的作用。尽管严格来说,真正归一化的不是𝑎,而是𝑧,深度学习文献中有一些争论,关于在激活函数之前是否应该将值𝑧归一化,或是否应该在应用激活函数𝑎后再规范值。实践中,经常做的是归一化𝑧,就是卷积层之后,激活函数之前。

Batch 归一化的作用是它适用的归一化过程,不只是输入层,甚至同样适用于神经网络中的深度隐藏层。应用 Batch 归一化了一些隐藏单元值中的平均值和方差,不过训练输入和这些隐藏单元值的一个区别是,也许不想隐藏单元值必须是平均值 0 和方差 1,标准化后还可以加两个参数alpha与beta进行调节,也可以调节其均值与方差值不再是标准的0与1。
为什么有效:
- 归一化可以加快学习速度
- 可以使权重比网络更滞后或更深层,减少了“Covariate shift”的问题(前一层参数改变影响后面的层)。Batch 归一化减少了输入值改变的问题,它的确使这些值变得更稳定,减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习
- 轻微正则化的效果:在 mini-batch 计算中,由均值
和方差缩放的,因为在 mini-batch 上计算的均值和方差,而不是在整个数据集上,均值和方差有一些小的噪声,对每一层的激活值加了少许噪声。正则化效果,因为给隐藏单元添加了噪音,这迫使后部单元不过分依赖任何一个隐藏单元。
总结:
- 在训练时,𝜇和𝜎2是在整个 mini-batch 上计算出来的包含了像是 64 或28 或其它一定数量的样本
- 在测试时,可能需要逐一处理样本,方法是根据训练集估算𝜇和𝜎2,估算的方式有很多种,理论上可以在最终的网络中运行整个训练集来得到𝜇和𝜎2,但在实际操作中,我通常运用指数加权平均来追踪在训练过程中你看到的𝜇和𝜎2的值。训练时候每个batch计算一个均值与方差,再基于指数加权平均的形式(优化算法中之前用到过)跟踪最新的均值与方差。
3.4 Softmax分类器
Softmax将逻辑回归推广到C类上,当C==2时,等同于逻辑回归。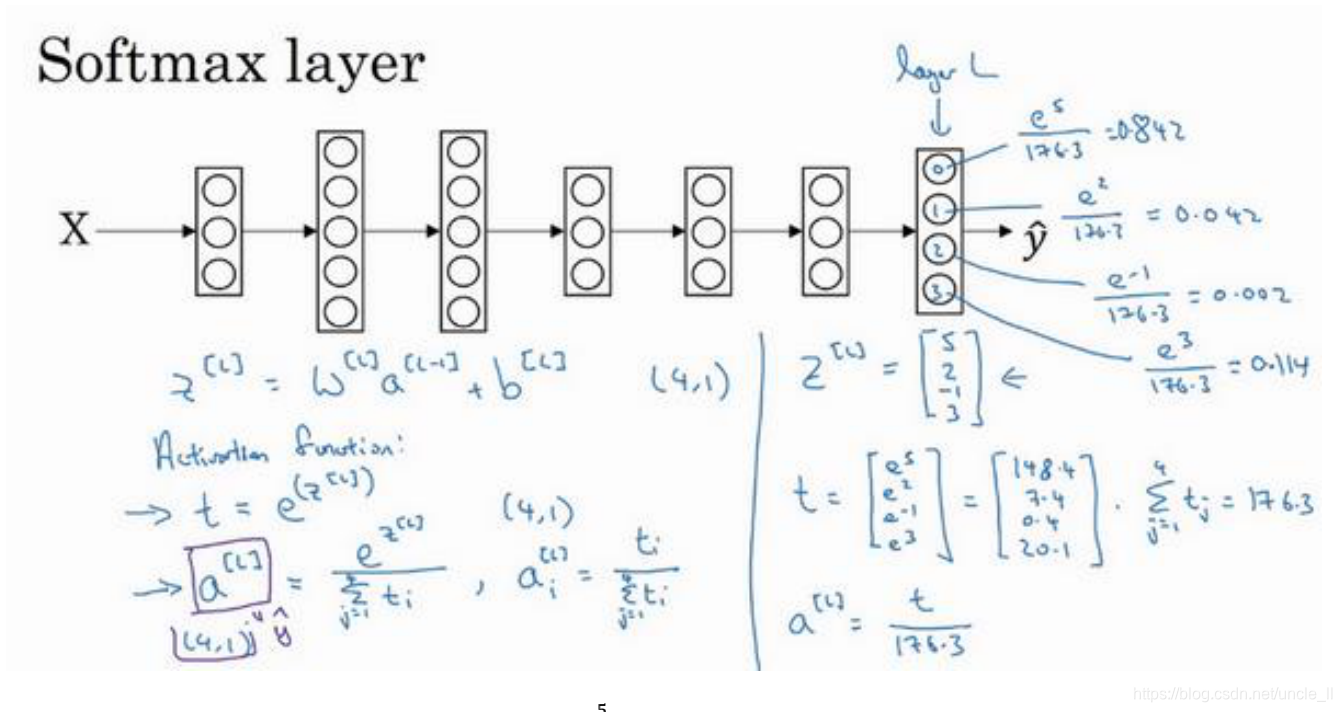
输出是多维向量,维度与类别数一致,表明属于每一类的概率值,相加为1。
softmax激活函数分为以下步骤:
- 线性激活 --> z=wx+b
- 求幂指数 --> tmp = e^z
- 归一化 --> a = tmp / total(tmp)

训练Softmax:
- 训练样本标签 类似于hardmax形式,属于哪一类,那个维度向量的index为1
- 损失函数为类似于逻辑回归的损失函数 -y log y'

损失函数所做的就是它找到训练集中的真实类别,然后试图使该类别相应的概率尽可能地高。这就是统计学中的极大似然估计。
3.5 深度学习框架

挑选原则:
- 便于编程
- 运行速度要快,训练等
- 是否真的开放:不仅需要开源,而且需要良好的管理
- 对应的编程语言:Python,Java 还是 C++
- 对应的任务应用:计算机视觉、自然语言处理或者线上广告