在上一篇文章《零基础入门深度学习(4):循环神经网络》中,我们介绍了循环神经网络以及它的训练算法。我们也介绍了循环神经网络很难训练的原因,这导致了它在实际应用中,很难处理长距离的依赖。在本文中,我们将介绍一种改进之后的循环神经网络:长短时记忆网络(Long Short Term Memory Network, LSTM),它成功地解决了原始循环神经网络的缺陷,成为当前最流行的RNN,在语音识别、图片描述、自然语言处理等许多领域中成功应用。
但不幸的一面是,LSTM的结构很复杂,因此,我们需要花上一些力气,才能把LSTM以及它的训练算法弄明白。在搞清楚LSTM之后,我们再介绍一种LSTM的变体:GRU (Gated Recurrent Unit)。 它的结构比LSTM简单,而效果却和LSTM一样好,因此,它正在逐渐流行起来。最后,我们仍然会动手实现一个LSTM。
长短时记忆网络是啥
我们首先了解一下长短时记忆网络产生的背景。回顾一下《零基础入门深度学习(4):循环神经网络》中推导的,误差项沿时间反向传播的公式:

梯度消失到底意味着什么?在《零基础入门深度学习(4):循环神经网络》中我们已证明,权重数组W最终的梯度是各个时刻的梯度之和,即:
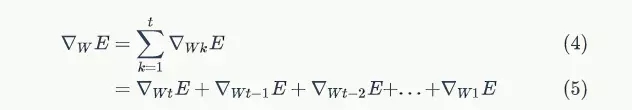
假设某轮训练中,各时刻的梯度以及最终的梯度之和如下图:

我们就可以看到,从上图的t-3时刻开始,梯度已经几乎减少到0了。那么,从这个时刻开始再往之前走,得到的梯度(几乎为零)就不会对最终的梯度值有任何贡献,这就相当于无论t-3时刻之前的网络状态h是什么,在训练中都不会对权重数组W的更新产生影响,也就是网络事实上已经忽略了t-3时刻之前的状态。这就是原始RNN无法处理长距离依赖的原因。
既然找到了问题的原因,那么我们就能解决它。从问题的定位到解决,科学家们大概花了7、8年时间。终于有一天,Hochreiter和Schmidhuber两位科学家发明出长短时记忆网络,一举解决这个问题。
其实,长短时记忆网络的思路比较简单。原始RNN的隐藏层只有一个状态,即h,它对于短期的输入非常敏感。那么,假如我们再增加一个状态,即c,让它来保存长期的状态,那么问题不就解决了么?如下图所示:
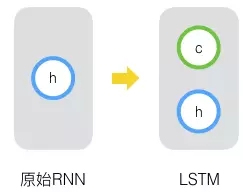
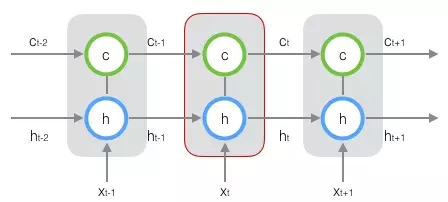
新增加的状态c,称为单元状态(cell state)。我们把上图按照时间维度展开:

LSTM的关键,就是怎样控制长期状态c。在这里,LSTM的思路是使用三个控制开关。第一个开关,负责控制继续保存长期状态c;第二个开关,负责控制把即时状态输入到长期状态c;第三个开关,负责控制是否把长期状态c作为当前的LSTM的输出。三个开关的作用如下图所示:
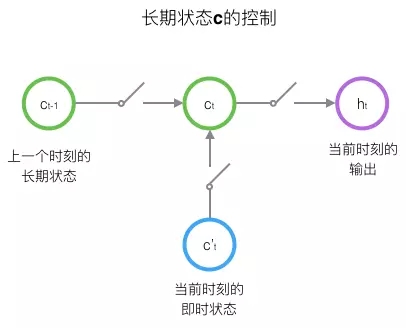
接下来,我们要描述一下,输出h和单元状态c的具体计算方法。
长短时记忆网络的前向计算
前面描述的开关是怎样在算法中实现的呢?这就用到了门(gate)的概念。门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。假设W是门的权重向量,是偏置项,那么门可以表示为:

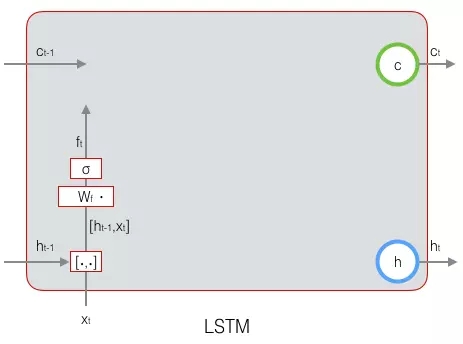
我们先来看一下遗忘门:

下图显示了遗忘门的计算:
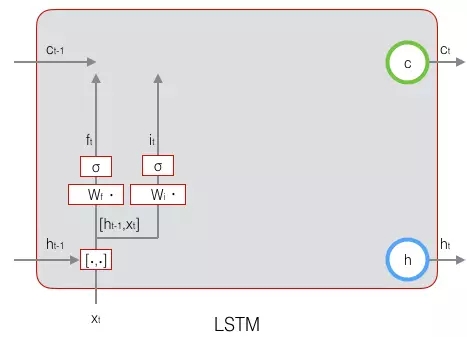
接下来看看输入门:
上式中,Wi是输入门的权重矩阵,bi是输入门的偏置项。下图表示了输入门的计算:

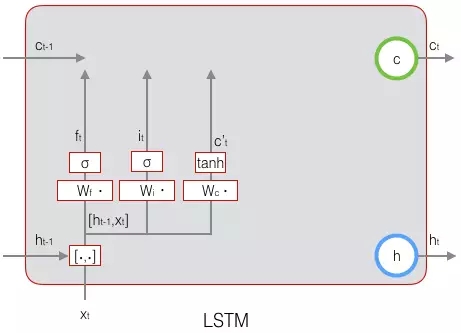


下图表示输出门的计算:
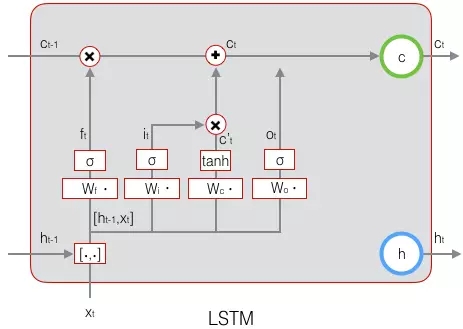
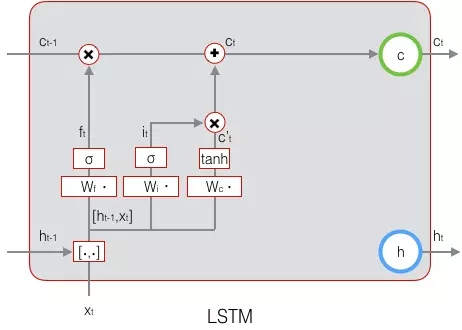
LSTM最终的输出,是由输出门和单元状态共同确定的:
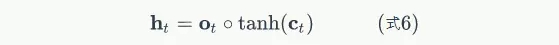
下图表示LSTM最终输出的计算:
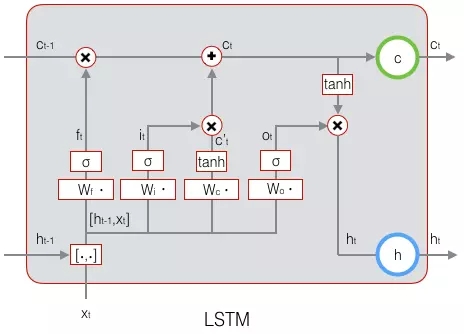
式1到式6就是LSTM前向计算的全部公式。至此,我们就把LSTM前向计算讲完了。
长短时记忆网络的训练
熟悉我们这个系列文章的同学都清楚,训练部分往往比前向计算部分复杂多了。LSTM的前向计算都这么复杂,那么,可想而知,它的训练算法一定是非常非常复杂的。现在只有做几次深呼吸,再一头扎进公式海洋吧。
LSTM训练算法框架
LSTM的训练算法仍然是反向传播算法,对于这个算法,我们已经非常熟悉了。主要有下面三个步骤:

关于公式和符号的说明
首先,我们对推导中用到的一些公式、符号做一下必要的说明。
接下来的推导中,我们设定gate的激活函数为sigmoid函数,输出的激活函数为tanh函数。他们的导数分别为:
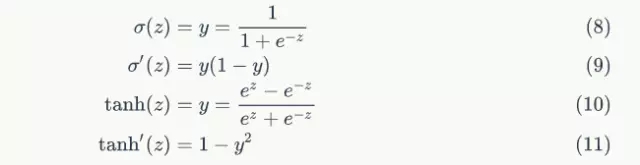
从上面可以看出,sigmoid和tanh函数的导数都是原函数的函数。这样,我们一旦计算原函数的值,就可以用它来计算出导数的值。



误差项沿时间的反向传递

下面,我们要把式7中的每个偏导数都求出来。根据式6,我们可以求出:

根据式4,我们可以求出:

因为:
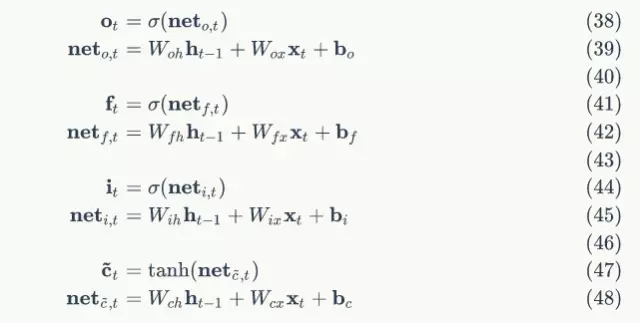
我们很容易得出:
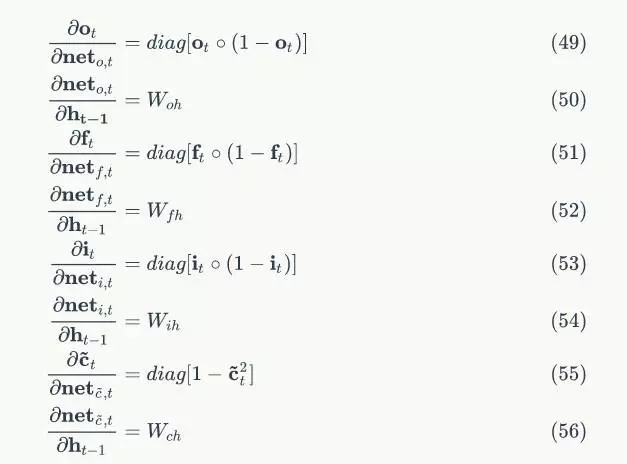
将上述偏导数带入到式7,我们得到:
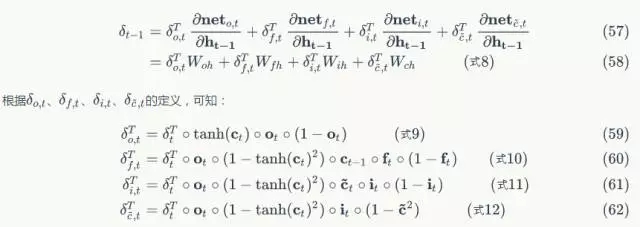
式8到式12就是将误差沿时间反向传播一个时刻的公式。有了它,我们可以写出将误差项向前传递到任意k时刻的公式:
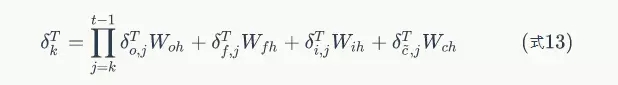
将误差项传递到上一层
我们假设当前为第l层,定义l-1层的误差项是误差函数对l-1层加权输入的导数,即:


式14就是将误差传递到上一层的公式。
权重梯度的计算
对于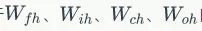 的权重梯度,我们知道它的梯度是各个时刻梯度之和(证明过程请参考文章《零基础入门深度学习(4) :循环神经网络》),我们首先求出它们在t时刻的梯度,然后再求出他们最终的梯度。
的权重梯度,我们知道它的梯度是各个时刻梯度之和(证明过程请参考文章《零基础入门深度学习(4) :循环神经网络》),我们首先求出它们在t时刻的梯度,然后再求出他们最终的梯度。
我们已经求得了误差项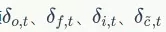 ,很容易求出t时刻的
,很容易求出t时刻的 :
:
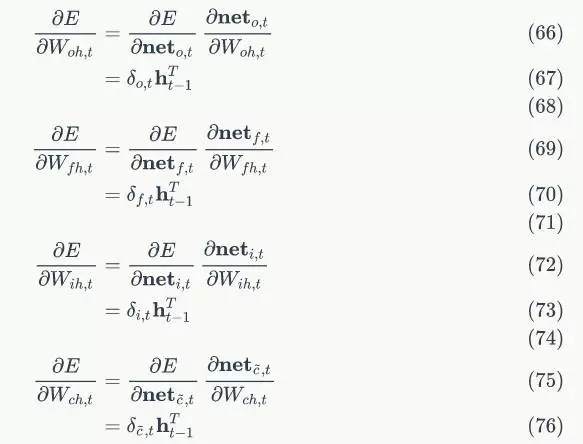
将各个时刻的梯度加在一起,就能得到最终的梯度:
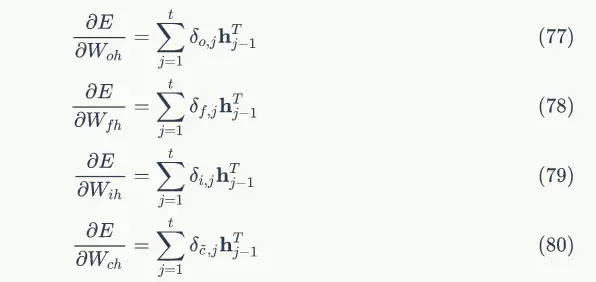
对于偏置项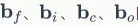 的梯度,也是将各个时刻的梯度加在一起。下面是各个时刻的偏置项梯度:
的梯度,也是将各个时刻的梯度加在一起。下面是各个时刻的偏置项梯度:
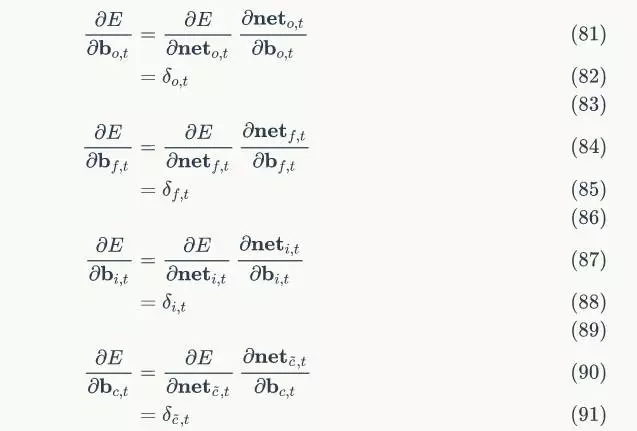
下面是最终的偏置项梯度,即将各个时刻的偏置项梯度加在一起:
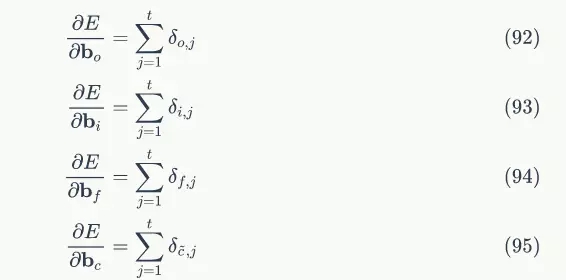
对于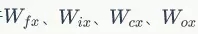 的权重梯度,只需要根据相应的误差项直接计算即可:
的权重梯度,只需要根据相应的误差项直接计算即可:
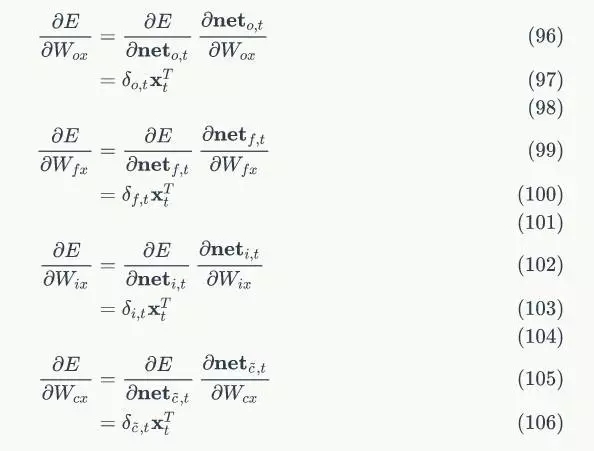
以上就是LSTM的训练算法的全部公式。因为这里面存在很多重复的模式,仔细看看,会发觉并不是太复杂。
当然,LSTM存在着相当多的变体,读者可以在互联网上找到很多资料。因为大家已经熟悉了基本LSTM的算法,因此理解这些变体比较容易,因此本文就不再赘述了。
长短时记忆网络的实现
在下面的实现中,LSTMLayer的参数包括输入维度、输出维度、隐藏层维度,单元状态维度等于隐藏层维度。gate的激活函数为sigmoid函数,输出的激活函数为tanh。
激活函数的实现
我们先实现两个激活函数:sigmoid和tanh。
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
class TanhActivator(object):
def forward(self, weighted_input):
return 2.0 / (1.0 + np.exp(-2 * weighted_input)) - 1.0
def backward(self, output):
return 1 - output * output
LSTM初始化
和前两篇文章代码架构一样,我们把LSTM的实现放在LstmLayer类中。
根据LSTM前向计算和方向传播算法,我们需要初始化一系列矩阵和向量。这些矩阵和向量有两类用途,一类是用于保存模型参数,例如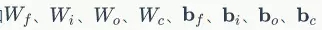 ;另一类是保存各种中间计算结果,以便于反向传播算法使用,它们包括
;另一类是保存各种中间计算结果,以便于反向传播算法使用,它们包括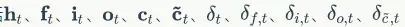 ,以及各个权重对应的梯度。
,以及各个权重对应的梯度。
在构造函数的初始化中,只初始化了与forward计算相关的变量,与backward相关的变量没有初始化。这是因为构造LSTM对象的时候,我们还不知道它未来是用于训练(既有forward又有backward)还是推理(只有forward)。
class LstmLayer(object):
def __init__(self, input_width, state_width,
learning_rate):
self.input_width = input_width
self.state_width = state_width
self.learning_rate = learning_rate
# 门的激活函数
self.gate_activator = SigmoidActivator()
# 输出的激活函数
self.output_activator = TanhActivator()
# 当前时刻初始化为t0
self.times = 0
# 各个时刻的单元状态向量c
self.c_list = self.init_state_vec()
# 各个时刻的输出向量h
self.h_list = self.init_state_vec()
# 各个时刻的遗忘门f
self.f_list = self.init_state_vec()
# 各个时刻的输入门i
self.i_list = self.init_state_vec()
# 各个时刻的输出门o
self.o_list = self.init_state_vec()
# 各个时刻的即时状态c~
self.ct_list = self.init_state_vec()
# 遗忘门权重矩阵Wfh, Wfx, 偏置项bf
self.Wfh, self.Wfx, self.bf = (
self.init_weight_mat())
# 输入门权重矩阵Wfh, Wfx, 偏置项bf
self.Wih, self.Wix, self.bi = (
self.init_weight_mat())
# 输出门权重矩阵Wfh, Wfx, 偏置项bf
self.Woh, self.Wox, self.bo = (
self.init_weight_mat())
# 单元状态权重矩阵Wfh, Wfx, 偏置项bf
self.Wch, self.Wcx, self.bc = (
self.init_weight_mat())
def init_state_vec(self):
'''
初始化保存状态的向量
'''
state_vec_list = []
state_vec_list.append(np.zeros(
(self.state_width, 1)))
return state_vec_list
def init_weight_mat(self):
'''
初始化权重矩阵
'''
Wh = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.state_width))
Wx = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.input_width))
b = np.zeros((self.state_width, 1))
return Wh, Wx, b
前向计算的实现
forward方法实现了LSTM的前向计算:
def forward(self, x):
'''
根据式1-式6进行前向计算
'''
self.times += 1
# 遗忘门
fg = self.calc_gate(x, self.Wfx, self.Wfh,
self.bf, self.gate_activator)
self.f_list.append(fg)
# 输入门
ig = self.calc_gate(x, self.Wix, self.Wih,
self.bi, self.gate_activator)
self.i_list.append(ig)
# 输出门
og = self.calc_gate(x, self.Wox, self.Woh,
self.bo, self.gate_activator)
self.o_list.append(og)
# 即时状态
ct = self.calc_gate(x, self.Wcx, self.Wch,
self.bc, self.output_activator)
self.ct_list.append(ct)
# 单元状态
c = fg * self.c_list[self.times - 1] + ig * ct
self.c_list.append(c)
# 输出
h = og * self.output_activator.forward(c)
self.h_list.append(h)
def calc_gate(self, x, Wx, Wh, b, activator):
'''
计算门
'''
h = self.h_list[self.times - 1] # 上次的LSTM输出
net = np.dot(Wh, h) + np.dot(Wx, x) + b
gate = activator.forward(net)
return gate
从上面的代码我们可以看到,门的计算都是相同的算法,而门和的计算仅仅是激活函数不同。因此我们提出了calc_gate方法,这样减少了很多重复代码。
反向传播算法的实现
backward方法实现了LSTM的反向传播算法。需要注意的是,与backword相关的内部状态变量是在调用backward方法之后才初始化的。这种延迟初始化的一个好处是,如果LSTM只是用来推理,那么就不需要初始化这些变量,节省了很多内存。
def backward(self, x, delta_h, activator):
'''
实现LSTM训练算法
'''
self.calc_delta(delta_h, activator)
self.calc_gradient(x)
算法主要分成两个部分,一部分使计算误差项:
def calc_delta(self, delta_h, activator):
# 初始化各个时刻的误差项
self.delta_h_list = self.init_delta() # 输出误差项
self.delta_o_list = self.init_delta() # 输出门误差项
self.delta_i_list = self.init_delta() # 输入门误差项
self.delta_f_list = self.init_delta() # 遗忘门误差项
self.delta_ct_list = self.init_delta() # 即时输出误差项
# 保存从上一层传递下来的当前时刻的误差项
self.delta_h_list[-1] = delta_h
# 迭代计算每个时刻的误差项
for k in range(self.times, 0, -1):
self.calc_delta_k(k)
def init_delta(self):
'''
初始化误差项
'''
delta_list = []
for i in range(self.times + 1):
delta_list.append(np.zeros(
(self.state_width, 1)))
return delta_list
def calc_delta_k(self, k):
'''
根据k时刻的delta_h,计算k时刻的delta_f、
delta_i、delta_o、delta_ct,以及k-1时刻的delta_h
'''
# 获得k时刻前向计算的值
ig = self.i_list[k]
og = self.o_list[k]
fg = self.f_list[k]
ct = self.ct_list[k]
c = self.c_list[k]
c_prev = self.c_list[k-1]
tanh_c = self.output_activator.forward(c)
delta_k = self.delta_h_list[k]
# 根据式9计算delta_o
delta_o = (delta_k * tanh_c *
self.gate_activator.backward(og))
delta_f = (delta_k * og *
(1 - tanh_c * tanh_c) * c_prev *
self.gate_activator.backward(fg))
delta_i = (delta_k * og *
(1 - tanh_c * tanh_c) * ct *
self.gate_activator.backward(ig))
delta_ct = (delta_k * og *
(1 - tanh_c * tanh_c) * ig *
self.output_activator.backward(ct))
delta_h_prev = (
np.dot(delta_o.transpose(), self.Woh) +
np.dot(delta_i.transpose(), self.Wih) +
np.dot(delta_f.transpose(), self.Wfh) +
np.dot(delta_ct.transpose(), self.Wch)
).transpose()
# 保存全部delta值
self.delta_h_list[k-1] = delta_h_prev
self.delta_f_list[k] = delta_f
self.delta_i_list[k] = delta_i
self.delta_o_list[k] = delta_o
self.delta_ct_list[k] = delta_ct
另一部分是计算梯度:
def calc_gradient(self, x):
# 初始化遗忘门权重梯度矩阵和偏置项
self.Wfh_grad, self.Wfx_grad, self.bf_grad = (
self.init_weight_gradient_mat())
# 初始化输入门权重梯度矩阵和偏置项
self.Wih_grad, self.Wix_grad, self.bi_grad = (
self.init_weight_gradient_mat())
# 初始化输出门权重梯度矩阵和偏置项
self.Woh_grad, self.Wox_grad, self.bo_grad = (
self.init_weight_gradient_mat())
# 初始化单元状态权重梯度矩阵和偏置项
self.Wch_grad, self.Wcx_grad, self.bc_grad = (
self.init_weight_gradient_mat())
# 计算对上一次输出h的权重梯度
for t in range(self.times, 0, -1):
# 计算各个时刻的梯度
(Wfh_grad, bf_grad,
Wih_grad, bi_grad,
Woh_grad, bo_grad,
Wch_grad, bc_grad) = (
self.calc_gradient_t(t))
# 实际梯度是各时刻梯度之和
self.Wfh_grad += Wfh_grad
self.bf_grad += bf_grad
self.Wih_grad += Wih_grad
self.bi_grad += bi_grad
self.Woh_grad += Woh_grad
self.bo_grad += bo_grad
self.Wch_grad += Wch_grad
self.bc_grad += bc_grad
print '-----%d-----' % t
print Wfh_grad
print self.Wfh_grad
# 计算对本次输入x的权重梯度
xt = x.transpose()
self.Wfx_grad = np.dot(self.delta_f_list[-1], xt)
self.Wix_grad = np.dot(self.delta_i_list[-1], xt)
self.Wox_grad = np.dot(self.delta_o_list[-1], xt)
self.Wcx_grad = np.dot(self.delta_ct_list[-1], xt)
def init_weight_gradient_mat(self):
'''
初始化权重矩阵
'''
Wh_grad = np.zeros((self.state_width,
self.state_width))
Wx_grad = np.zeros((self.state_width,
self.input_width))
b_grad = np.zeros((self.state_width, 1))
return Wh_grad, Wx_grad, b_grad
def calc_gradient_t(self, t):
'''
计算每个时刻t权重的梯度
'''
h_prev = self.h_list[t-1].transpose()
Wfh_grad = np.dot(self.delta_f_list[t], h_prev)
bf_grad = self.delta_f_list[t]
Wih_grad = np.dot(self.delta_i_list[t], h_prev)
bi_grad = self.delta_f_list[t]
Woh_grad = np.dot(self.delta_o_list[t], h_prev)
bo_grad = self.delta_f_list[t]
Wch_grad = np.dot(self.delta_ct_list[t], h_prev)
bc_grad = self.delta_ct_list[t]
return Wfh_grad, bf_grad, Wih_grad, bi_grad, \
Woh_grad, bo_grad, Wch_grad, bc_grad
梯度下降算法的实现
下面是用梯度下降算法来更新权重:
def update(self):
'''
按照梯度下降,更新权重
'''
self.Wfh -= self.learning_rate * self.Whf_grad
self.Wfx -= self.learning_rate * self.Whx_grad
self.bf -= self.learning_rate * self.bf_grad
self.Wih -= self.learning_rate * self.Whi_grad
self.Wix -= self.learning_rate * self.Whi_grad
self.bi -= self.learning_rate * self.bi_grad
self.Woh -= self.learning_rate * self.Wof_grad
self.Wox -= self.learning_rate * self.Wox_grad
self.bo -= self.learning_rate * self.bo_grad
self.Wch -= self.learning_rate * self.Wcf_grad
self.Wcx -= self.learning_rate * self.Wcx_grad
self.bc -= self.learning_rate * self.bc_grad
梯度检查的实现
和RecurrentLayer一样,为了支持梯度检查,我们需要支持重置内部状态:
def reset_state(self):
# 当前时刻初始化为t0
self.times = 0
# 各个时刻的单元状态向量c
self.c_list = self.init_state_vec()
# 各个时刻的输出向量h
self.h_list = self.init_state_vec()
# 各个时刻的遗忘门f
self.f_list = self.init_state_vec()
# 各个时刻的输入门i
self.i_list = self.init_state_vec()
# 各个时刻的输出门o
self.o_list = self.init_state_vec()
# 各个时刻的即时状态c~
self.ct_list = self.init_state_vec()
最后,是梯度检查的代码:
def data_set():
x = [np.array([[1], [2], [3]]),
np.array([[2], [3], [4]])]
d = np.array([[1], [2]])
return x, d
def gradient_check():
'''
梯度检查
'''
# 设计一个误差函数,取所有节点输出项之和
error_function = lambda o: o.sum()
lstm = LstmLayer(3, 2, 1e-3)
# 计算forward值
x, d = data_set()
lstm.forward(x[0])
lstm.forward(x[1])
# 求取sensitivity map
sensitivity_array = np.ones(lstm.h_list[-1].shape,
dtype=np.float64)
# 计算梯度
lstm.backward(x[1], sensitivity_array, IdentityActivator())
# 检查梯度
epsilon = 10e-4
for i in range(lstm.Wfh.shape[0]):
for j in range(lstm.Wfh.shape[1]):
lstm.Wfh[i,j] += epsilon
lstm.reset_state()
lstm.forward(x[0])
lstm.forward(x[1])
err1 = error_function(lstm.h_list[-1])
lstm.Wfh[i,j] -= 2*epsilon
lstm.reset_state()
lstm.forward(x[0])
lstm.forward(x[1])
err2 = error_function(lstm.h_list[-1])
expect_grad = (err1 - err2) / (2 * epsilon)
lstm.Wfh[i,j] += epsilon
print 'weights(%d,%d): expected - actural %.4e - %.4e' % (
i, j, expect_grad, lstm.Wfh_grad[i,j])
return lstm
我们只对做了检查,读者可以自行增加对其他梯度的检查。下面是某次梯度检查的结果:

GRU
前面我们讲了一种普通的LSTM,事实上LSTM存在很多变体,许多论文中的LSTM都或多或少的不太一样。在众多的LSTM变体中,GRU (Gated Recurrent Unit)也许是最成功的一种。它对LSTM做了很多简化,同时却保持着和LSTM相同的效果。因此,GRU最近变得越来越流行。
GRU对LSTM做了两个大改动:
-
将输入门、遗忘门、输出门变为两个门:更新门(Update Gate)Zt和重置门(Reset Gate)rt。
-
将单元状态与输出合并为一个状态:h。
GRU的前向计算公式为:
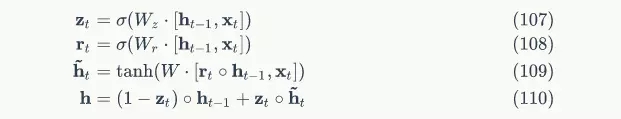
下图是GRU的示意图:
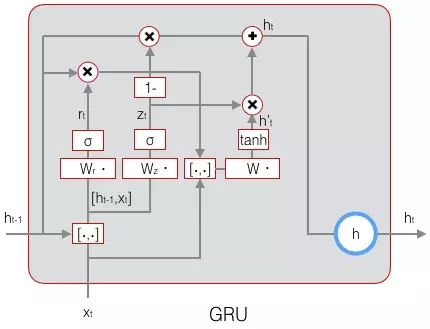
GRU的训练算法比LSTM简单一些,留给读者自行推导,本文就不再赘述了。
小结
至此,LSTM——也许是结构最复杂的一类神经网络——就讲完了,相信拿下前几篇文章的读者们搞定这篇文章也不在话下吧!现在我们已经了解循环神经网络和它最流行的变体——LSTM,它们都可以用来处理序列。但是,有时候仅仅拥有处理序列的能力还不够,还需要处理比序列更为复杂的结构(比如树结构),这时候就需要用到另外一类网络:递归神经网络(Recursive Neural Network),巧合的是,它的缩写也是RNN。在下一篇文章中,我们将介绍递归神经网络和它的训练算法。
原文:https://zybuluo.com/hanbingtao/note/581764



