排序算法
Tool implement
//generate a array of n elements, range [rangL, rangeR]
int *generateRandomArray(int n, int rangL, int rangeR) {
assert(rangeR >= rangL);
int *arr = new int[n];
srand(time(NULL));
for (int i = 0; i < n; i++) {
arr[i] = rand() % (rangeR - rangL + 1) + rangL;
}
return arr;
}
template<typename T>
void showArray(T arr[], int n) {
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
生成随机的n个数量的数组,输出数组每一个元素的内容。测试排序算法使用的标准就是运行时间和排序的正确性,所以需要一个验证正确性和计算排序时间的:
template<typename T>
void testSort( string sortName, void(*sort)(T[], int), T arr[], int n){
clock_t startTime = clock();
sort(arr, n);
clock_t endTime = clock();
if (isSorted(arr, n)){
cout << sortName << ": " << double(endTime - startTime)/CLOCKS_PER_SEC << "s" << endl;
} else
cout << "sort function is wrong!" << endl;
return;
}
template<typename T>
bool isSorted(T arr[], int n){
for (int i = 0; i < n-1; i++){
if (arr[i] > arr[i+1])
return false;
}
return true;
}
) 的排序
的排序
这种算法应该是属于比较慢的算法了,编码简单,易于实现,是一些简单场景的选择。在一些特殊情况下,简单的排序算法更容易实现且更有效。从简单的算法演变到复杂的算法,循序渐进,作为子过程改进跟复杂的算法。
选择排序——SelectionSort
选择排序比较简单,如果是最简单的一个了。基本思想就是遍历每一个位置,选择这个位置之后最小的元素与当前元素对换:


代码实现:
template<typename T>
void SelectionSort(T arr[], int n) {
for (int i = 0; i < n; i++) {
int minIndex = i;
for (int j = i; j < n; j++) {
if (arr[j] < arr[minIndex])
minIndex = j;
}
swap(arr[minIndex], arr[i]);
}
}
由于是模板类,所以还可以用来排序string,运算符重载还可以用来对类排序。
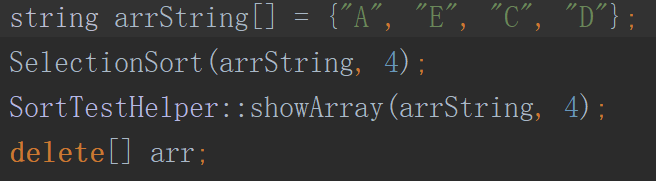
定义一个学生类用于排序:
struct student{
string name;
float score;
bool operator<(const student &otherStudent){
return score < otherStudent.score;
}
friend ostream& operator<<(ostream &os, const student &otherStudent){
os << "Student: " << otherStudent.name << " " << otherStudent.score << endl;
return os;
}
};


插入排序——InsertionSort
插入排序也是一个的排序算法。


template<typename T>
void InsertionSort(T arr[], int n){
for (int i = 1; i < n; i ++){
for (int j = i; j > 0; j --){
if (arr[j] < arr[j-1]){
swap(arr[j], arr[j-1]);
} else
break;
}
}
}
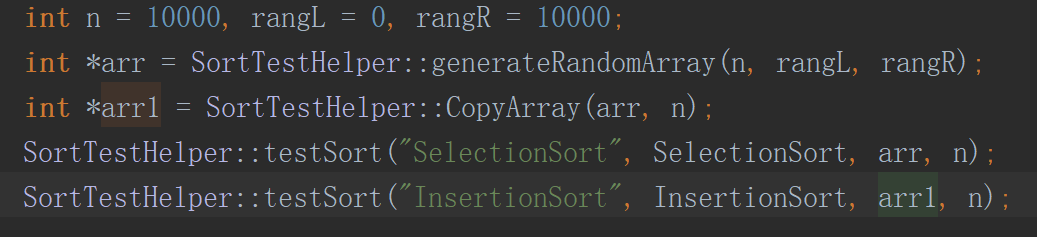
代码实现:
template<typename T>
void InsertionSort_version2(T arr[], int n){
for (int i = 1; i < n; i ++){
T temp = arr[i];
int j = 0;
for (j = i; j > 0 && arr[j-1] > temp; j --){
arr[j] = arr[j-1];
}
arr[j] = temp;
}
对于插入排序还有一个比较好的性质,如果当前数组是一个基本有序的数组那么基本插入排序每一次就基本被终止了,那么就会很快。
) 的排序
的排序
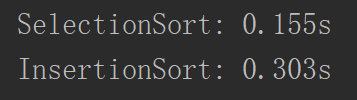
在小数据量的情况下,两者的差别都不会特别大,但是当数据量变大的时候,两者的差别就会越来越大了。
归并排序——MergeSort
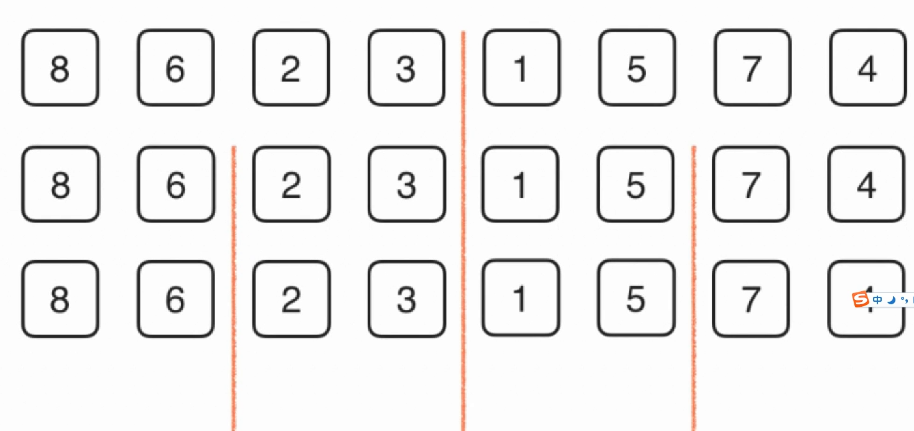
步骤其实很简单,首先进行划分,当划分到一定的细度的时候就不能划分了,然后就进行归并
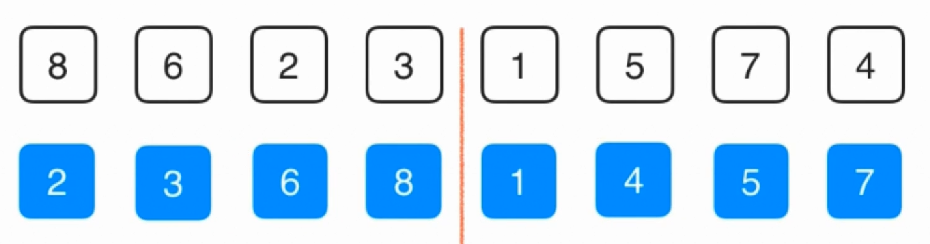


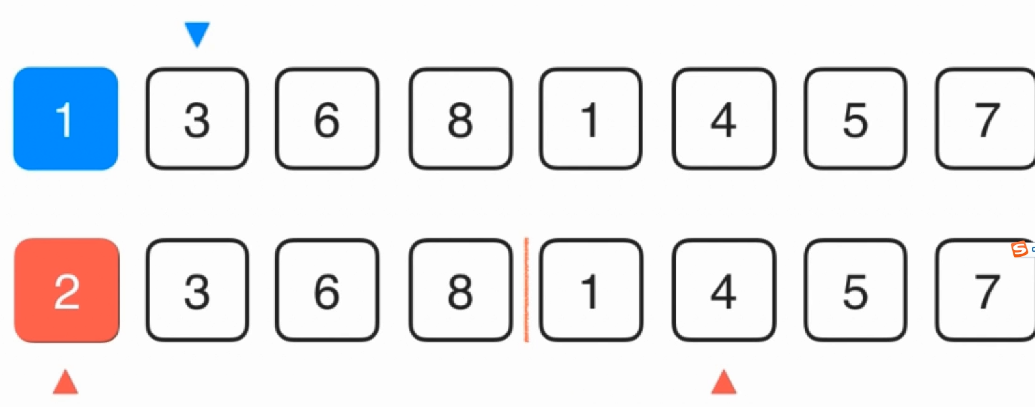
template<typename T>
void __merge(T arr[], int l, int mid, int r) {
T *temp = new T[r-l+1];
for (int i = l; i <= r; i++) {
temp[i - l] = arr[i];
}
int i = l, j = mid + 1;
for (int k = l; k <= r; k++) {
if (i > mid) {
arr[k] = temp[j - l];
j++;
} else if (j > r) {
arr[k] = temp[i - l];
i++;
} else if (temp[i - l] < temp[j - l]) {
arr[k] = temp[i - l];
i++;
} else {
arr[k] = temp[j - l];
j++;
}
}
delete[] temp;
}
template<typename T>
void __mergeSort(T arr, int l, int r) {
if (l >= r) {
return;
} else {
int mid = (l + r) / 2;
__mergeSort(arr, l, mid);
__mergeSort(arr, mid + 1, r);
__merge(arr, l, mid, r);
}
}
template<typename T>
void MergeSort(T arr[], int n) {
__mergeSort(arr, 0, n - 1);
}
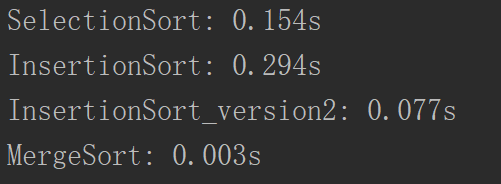
可以看到对于一万个数组排序的时间很快,其实归并排序就是典型的用空间换时间的,每一次递归就开了一个空间,每一次递归的时候还有一个缓冲数组,所以使用的空间复杂度比一般的排序算法要大。
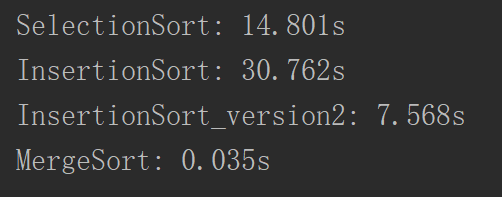
但是对于这个代码来说,还是可以优化的,因为在归并的时候,我们是无论两边的数组是个什么情况都进行一个归并,但是事实上这样是不严谨的,因为事实上如果一边的最大的元素小于另一边的最小的元素,就可以说完全大于了,所以加上判断:
void __mergeSort(T arr, int l, int r) {
if (l >= r) {
return;
} else {
int mid = (l + r) / 2;
__mergeSort(arr, l, mid);
__mergeSort(arr, mid + 1, r);
if (arr[mid] > arr[mid + 1]) {
__merge(arr, l, mid, r);
}
}
}
加上一个判断即可。
自底向上的归并排序——upMergeSort
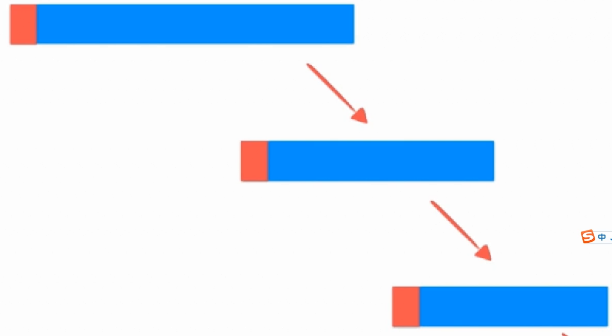
其实思想都是一样的,都是分而治之的思想,先两个两个的排,然后四个四个的排,然后八个八个的排,以此类推:
先两个两个的排,然后四个四个:

之后8个一起,这个过程其实不需要递归,直接迭代实现即可。
template<typename T>
void upMergeSort(T arr[], int n){
for (int sz = 1; sz <= n; sz = sz + sz){
for (int i = 0; i + sz < n; i += sz + sz){
__merge(arr, i, i+sz-1, min(i+sz+sz-1, n-1));
}
}
}
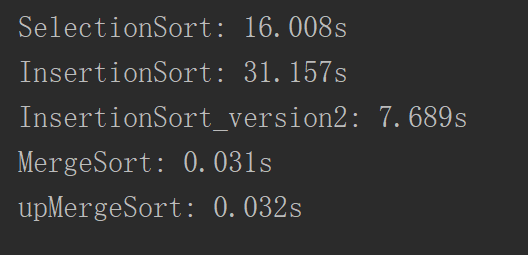
时间差不多。
快速排序——QuickSort
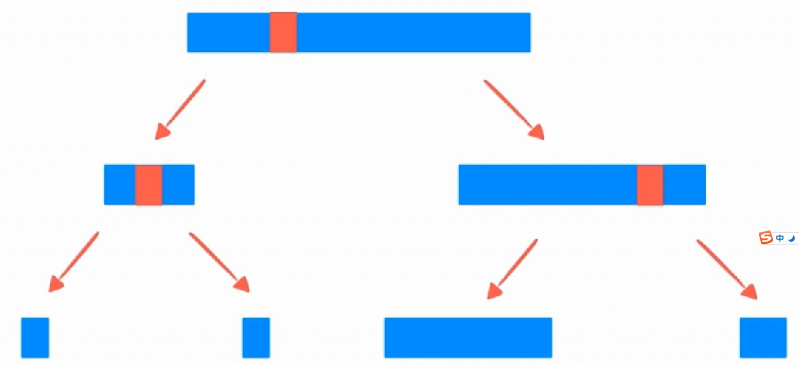
归并排序和快速排序不同的就是,归并排序是无论什么情况直接就一分为二两部分,快速排序也是分成两部分,但是快速排序是先找到对应的一个元素的位置,然后直接找到这个元素应该在的位置:
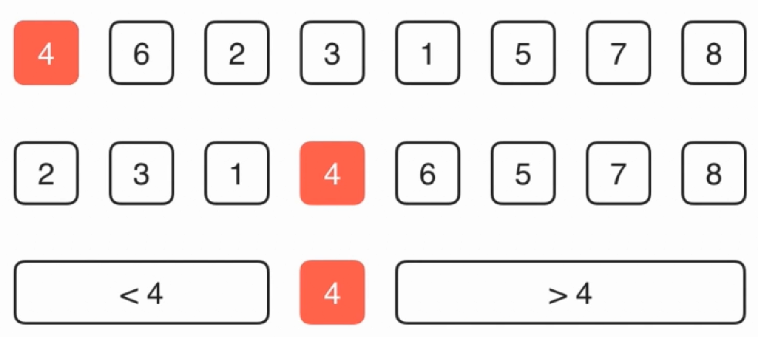

代码实现:
template<typename T>
int __partition(T arr[], int l, int r) {
T v = arr[l];
int j = l;
for (int i = l + 1; i <= r; i++) {
if (arr[i] < v) {
swap(arr[j + 1], arr[i]);
j++;
}
}
swap(arr[j], arr[l]);
return j;
}
template<typename T>
void __quickSort(T arr[], int l, int r) {
if (l >= r) {
return;
}
int p = __partition(arr, l, r);
__quickSort(arr, l, p - 1);
__quickSort(arr, p + 1, r);
}
template<typename T>
void QuickSort(T arr[], int n) {
__quickSort(arr, 0, n - 1);
}
template<typename T>
int __partition(T arr[], int l, int r) {
swap(arr[l], arr[rand()%(r-l+1)+l]);
T v = arr[l];
int j = l;
for (int i = l + 1; i <= r; i++) {
if (arr[i] < v) {
swap(arr[j + 1], arr[i]);
j++;
}
}
效果就不出了。
接下来还有一个问题,如果这个数组是一个基本有序的数组,测试一下数据:

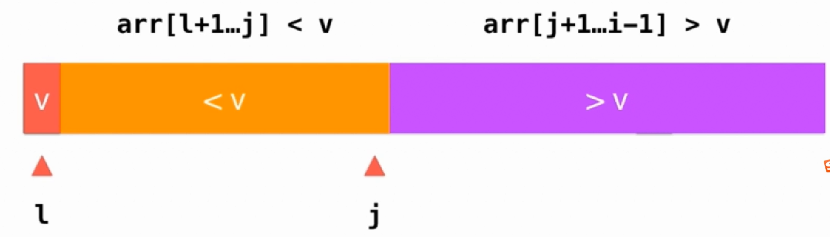
可以看到快速排序还是慢了点。为什么会这样,我们考虑一下partition函数:


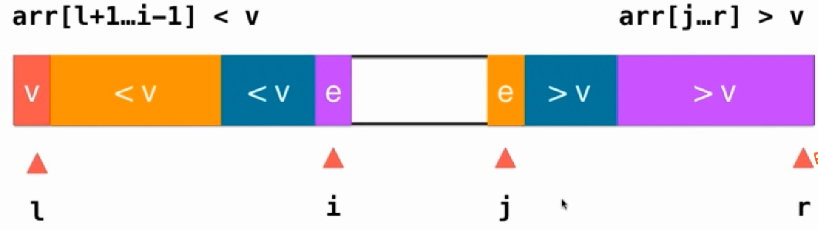
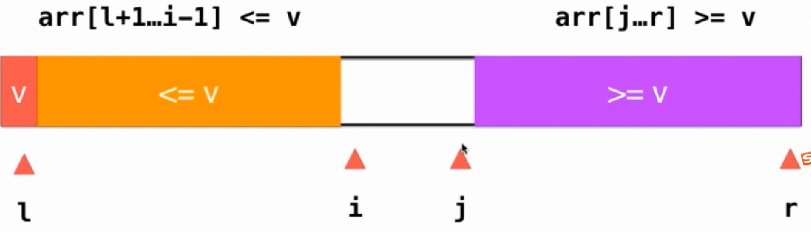
按照如上的这一种结构就算是有大量的重复的数值也可以平均分开,达到两边是相同的数量。
代码实现:
template<typename T>
int __partition_version2(T arr[], int l, int r) {
swap(arr[l], arr[rand() % (r - l + 1) + l]);
T v = arr[l];
int i = l+1, j = r;
while (true){
while (i <= r && arr[i] < v){
i++;
}
while (j >= l+1 && arr[j] > v){
j--;
}
if (i > j){
break;
} else{
swap(arr[i], arr[j]);
i++;
j--;
}
}
swap(arr[l], arr[j]);
return j;
}
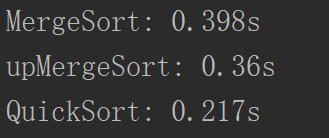
这样效果就好很多了。
实现带有重复元素的数组快速排序还有一个更加经典的实现方法,就是三路排序了。
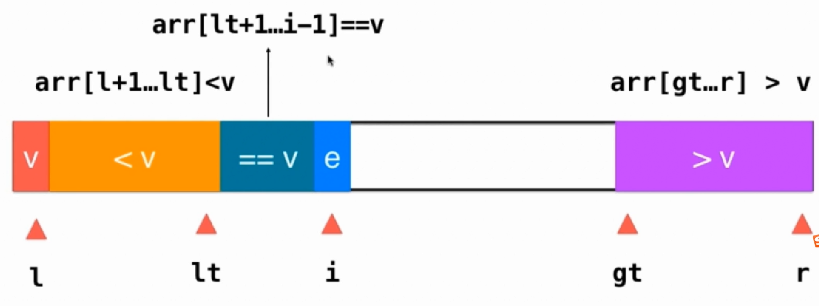
代码实现:
template<typename T>
int __partition_version3(T arr[], int l, int r){
swap(arr[l], arr[rand() % (r - l + 1) + l]);
T v = arr[l];
int lt = l, gt = r+1, i = l+1;
while (i < gt){
if (arr[i] < v){
swap(arr[i], arr[lt+1]);
lt++;
i++;
} else if (arr[i] > v){
swap(arr[i], arr[gt-1]);
gt--;
} else{
i++;
}
}
swap(arr[l], arr[lt]);
return lt;
}
堆排序——HeapSort
堆是一种比较常用的数据结构,常用的堆有二叉堆,费波纳茨堆等等。堆是一颗完全二叉树,除了最后一层其他的每一层都是满的,而最后一层都的子节点都是集中在了左边。堆的实现在DataStructure里面提到,实现很简单。因为实现的是最大堆,出来的元素就是最大的:
using namespace std;
template<typename T>
void HeapSort_version1(T arr[], int n){
MaxHeap<T> heap = MaxHeap<T>(n);
for (int i = 0; i < n; ++i) {
heap.insert(arr[i]);
}
for (int j = n-1; j >= 0; --j) {
arr[j] = heap.pop();
}
}
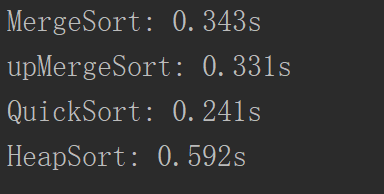
但是有一个小问题,每一次都是插入这样效率不高,所以我们可以直接在原数组上操作
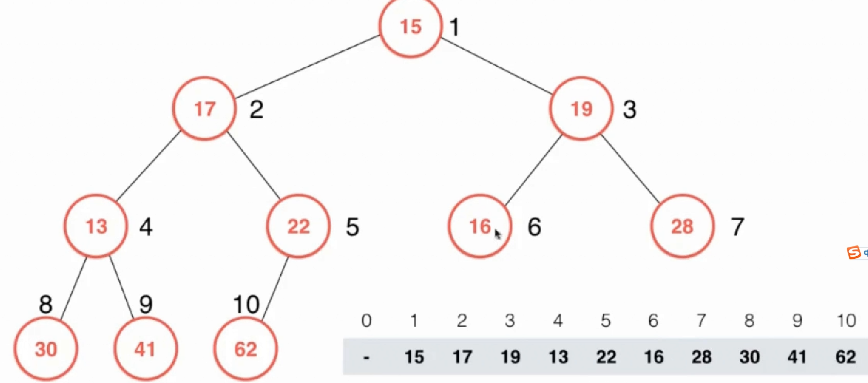
比如这就并不是一个正确的最大堆,需要用heapify转变一下。注意到每一个叶子都是一个堆,而且是符合规定的堆,所以肯定是从最底层开始。第一个不是堆的节点一定是最后一个叶子除2。所以第一个要做的就是对第一个不是堆的节点进行排序,很明显就是22这个元素了,对比交换,这个过程其实就是一个shitDown的过程,而我们要shitdown的元素是那5个不是堆的元素,所以对于这个数组直接做5次循环对每一个不是堆的元素进行shiftDown操作即可。
MaxHeap(item arr[], int n){
data = new item[n+1];
capacity = n;
for (int i = 0; i < n; ++i) {
data[i+1] = arr[i];
}
count = n;
for (int j = count/2; j >= 1; --j) {
shiftDown(j);
}
}
之后就可以使用heapify来代替迭代插入,其实效果差别不大。堆排序在现实中其实蛮少用到的,常用的还是对于动态数据结构的维护。
事实上这个版本的和上一个版本的差别是不大的。刚刚的一个一个元素插入堆里面的计算复杂度是


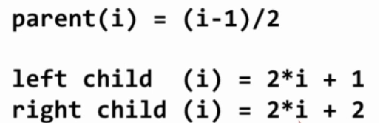
template<typename T>
void __shiftDown(T arr[], int n, int i){
while (2*i + 1 < n){
int change = 2*i + 1;
if (change + 1 < n && arr[change] < arr[change+1]){
change ++;
}
if (arr[i] >= arr[change]){
break;
}
swap(arr[i], arr[change]);
i = change;
}
}
接下了就是按照上述流程排序:
template<typename T>
void HeapSort_version2(T arr[], int n) {
//heapify,create a max heap;
for (int i = (n-1)/2; i >= 0; --i) {
__shiftDown(arr, n, i);
}
for (int j = n-1; j > 0 ; --j) {
swap(arr[0], arr[j]);
__shiftDown(arr, j, 0);
}
}
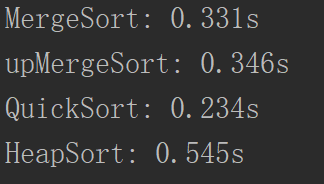
看看效果:
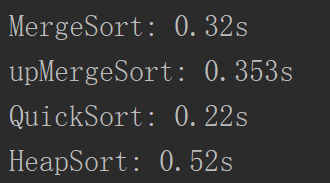
差别不是特别大,但是总的来说还是快了,因为它不需要进行额外的空间,也不需要赋值的操作等等,相对会快点。
排序算法总结
| 平均时间复杂度 | 原地排序 | 额外空间 | 稳定性 | |
|---|---|---|---|---|
| Insertion Sort | 是 | 是 | ||
| Merge Sort | 否 | 是 | ||
| Quick Sort | 是 | 否 | ||
| Heap Sort | 是 | 否 |
快速排序的额外空间是logn,因为递归的次数就是logn,而每一次递归就需要一个栈空间来存储。
最后附上GitHub代码:https://github.com/GreenArrow2017/DataStructure/tree/master/SortAlgorithm