在我们解决一些问题时,我们需要将所给的数据排序。排序算法也是一门基础算法,排序有许多种:冒泡排序,插入排序,选择排序,桶排序,快速排序,归并排序,希尔排序,堆排序,拓扑排序等(最后两种以后学数据结构和图论再讲)。
今天,我们就来走进第一个排序——冒泡排序。
我们先来看一个图:
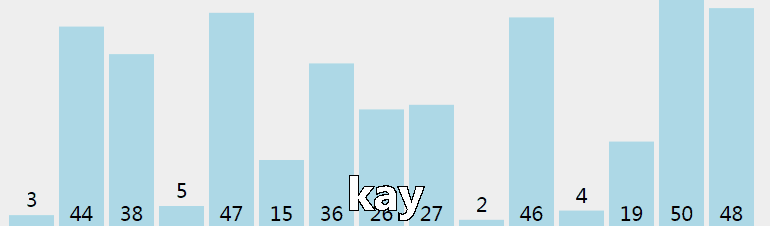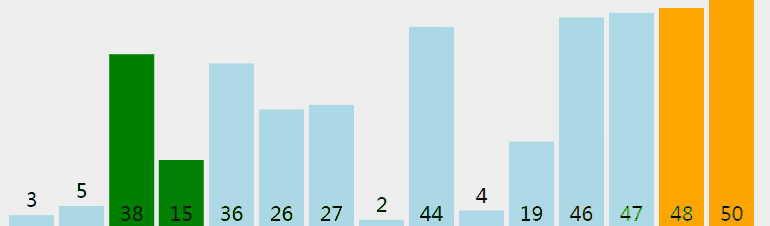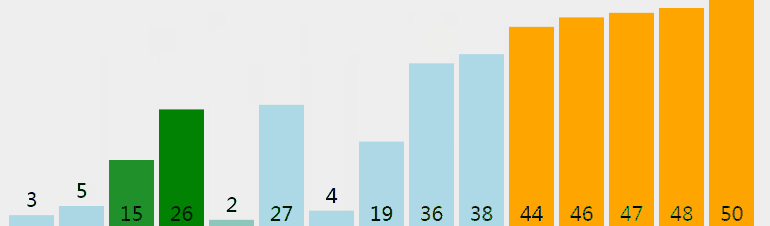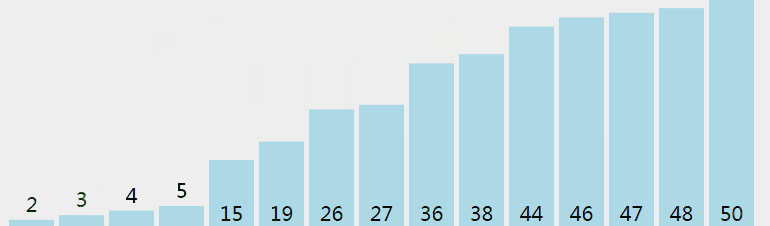
这就是冒泡排序的基本原理。第一层循环从n~2,第二层循环枚举第j和第j+1个数(1<=j<i),若a[ij>a[j+1],就叫换他们俩。(这里是从小到大升序排列)
这样,每执行完一个外层循环就确定第i个数(2<=i<=n),最终方可之其结果。
让我们来看代码:
#include<iostream>
using namespace std;
int n,a[10001];
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=n;i>1;i--)
for(int j=1;j<i;j++)
if(a[j]>a[j+1])
swap(a[j],a[j+1]);
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}这个算法的复杂度是O(n^2),两层循环,时间复杂度还比较高。我们想来看看大数据的效率。
直接在代码中加一些代码:
#include<iostream>
#include<ctime>
using namespace std;
int n,a[10001];
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
int main()
{
int start=clock();//开始时间
freopen("num.txt","r",stdin);//用freopen增加程序输入效率
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=n;i>1;i--)
for(int j=1;j<i;j++)
if(a[j]>a[j+1])
swap(a[j],a[j+1]);
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
cout<<endl;
int end=clock();//结束时间
cout<<"Run time in"<<end-start<<"ms"<<endl;
return 0;
}由于我们的电脑不同,所以所测试间不同。其实,我们这个算法还是不够好的,我们可以进行优化。
比如说6个数:2,1,4,6,3,5 我们来排序。
冒泡第一轮:
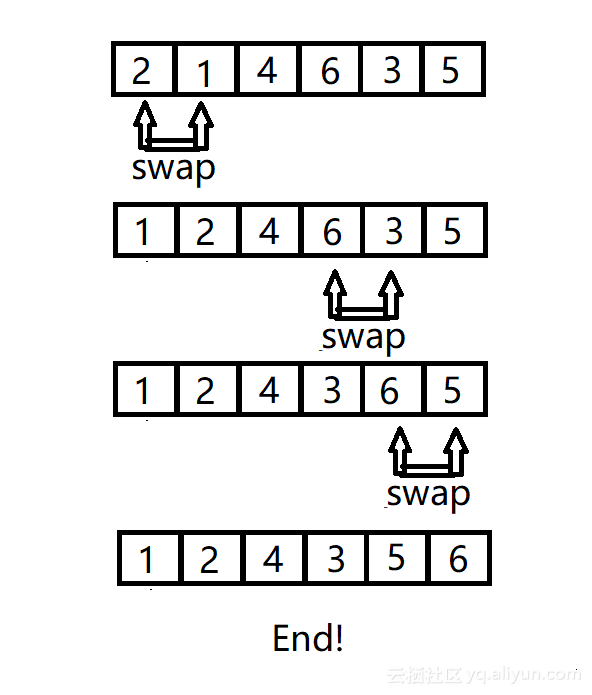
第二轮:
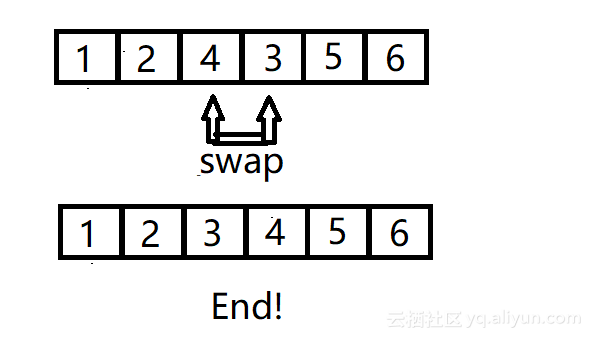
接下来,我们不难发现,序列已经排好,之后的循环都是不必要的!!!
既然是不必要,我们就把它删了呗!
优化流程:
用一个bool变量判断是否有交换。初始化为0,交换了,就变成1。这一层循环结束之后,若它还是0,也就是没有交换,直接退出。
代码如下:
#include<iostream>
using namespace std;
int n,a[10001];
bool v=0;
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=n;i>1;i--){
v=0;
for(int j=1;j<i;j++)
if(a[j]>a[j+1]){
swap(a[j],a[j+1]);
v=1;
}
if(!v)//v=0
break;//跳出循环
}
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
cout<<endl;
return 0;
}虽然不是每组数据都能优化,但是总有节约时间的地方。
我们还能将它写成函数形式:
void bubble_sort(int n,int a[]){
for(int i=n;i>=1;i--){
bool v=0;
for(int j=1;j<i;j++)
if(a[j]>a[j+1]){
swap(a[j],a[j]+1);
v=1;
}
if(!v){
break;
}
}
return;
}到这里,冒泡排序的介绍就结束了。那么,大家会不会有疑问:这个冒泡排序效率不是最高的,也不是最方便的,学他干什么呢?不是浪费时间吗?
其实不是。任何一种算法都有他立足与信息学世界的理由。
冒泡排序的实质就是将相邻两个数交换,于是,我们可以利用这一点来求解特定的问题。
栗1.2.1-1 洛谷P1116 车厢重组
https://www.luogu.org/problemnew/show/P1116
题目描述
在一个旧式的火车站旁边有一座桥,其桥面可以绕河中心的桥墩水平旋转。一个车站的职工发现桥的长度最多能容纳两节车厢,如果将桥旋转180度,则可以把相邻两节车厢的位置交换,用这种方法可以重新排列车厢的顺序。于是他就负责用这座桥将进站的车厢按车厢号从小到大排列。他退休后,火车站决定将这一工作自动化,其中一项重要的工作是编一个程序,输入初始的车厢顺序,计算最少用多少步就能将车厢排序。
输入输出格式
输入格式:
共两行。
车厢总数N,N<=10000
第二行是N个不同的数表示初始的车厢顺序。
输出格式:
一个整数,最少的旋转次数。
输入输出样例
4 4 3 2 1
6
不难看出,这题要用冒泡排序来求解。
我们每交换一次,Ans++,表示旋转次数++。这题就迎刃而解了。
来看代码吧:
#include<iostream>
using namespace std;
int n,a[10001],Ans=0;
bool v=0;
void swap(int &a,int &b)
{
int t=a;
a=b;
b=t;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=n;i>1;i--){
v=0;
for(int j=1;j<i;j++)
if(a[j]>a[j+1]){
swap(a[j],a[j+1]);
v=1;
Ans++;
}
if(!v)
break;
}
cout<<Ans<<endl;
return 0;
}这题就这么过了吧,也没太大难度。
但是,我们不应该这么过。一位叫小学生的洛谷用户提供了这样的算法:
作者: 小学生 更新时间: 2018-04-26 08:44 在Ta的博客查看
-
我看了其他题解都是做了排序,可是题目只是问需要多少次移动,没问排序结果啊!!!
-
所以我没有做排序,只是迭代去计算每个数字前有几个数字比它大,这意味着它必须要移动几次。
-
没有做冒泡排序,双层循环写法也和冒泡无关。
#include <iostream>
using namespace std;
int n, sum;
int main()
{
cin >> n;
int a[n];
for (int i = 0; i < n; ++i)
cin >> a[i];
for (int i = 0; i < n; ++i)
for (int j = 0; j < i; ++j)
if (a[j] > a[i])
++sum;
cout << sum;
return 0;
}我们看看他的算法。
第一眼望过去,貌似是错的。没有改变之前的状态,后面怎么排序呢?
好吧,他说了,不用排序。其实思想跟冒泡排序没太大差别。
我们想一想,假设有n个数,6,5,4,3,2,1。
在6后面,有5个比6小的数,就要旋转5次,
在5后面,有4个比5小的数,就要旋转4次,
······
在1后面,有0个比1小的数,就要旋转0次,
SO,Ans=0+1+2+3+4+5=15。
结果完全一样。
好了,今天的内容就到这里,我们下一期将给大家介绍插入排序,我们下次见!