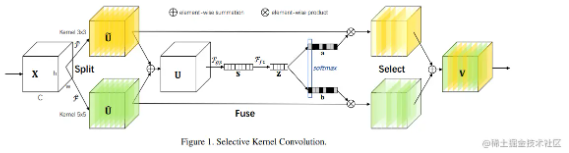
论文动机
驻留在图的不同部分中的节点可能在其本地网络拓扑中具有类似的结构角色。然而学习节点的结构表示是一项具有挑战性的无监督学习任务,其通常涉及为每个节点人工指定和定制拓扑特征。
GraphWave 是一种可扩展的无监督方法,用于基于网络中的结构相似性来学习节点嵌入。GraphWave 通过将小波视为概率分布并使用经验特征函数表征分布来开发光谱图小波的新用途。
GraphWave 提供理论保证,具有相似本地网络邻域的节点将具有类似的 GraphWave 嵌入,即使这些节点可能驻留在网络的非常不同的部分中。 GraphWave 与边数成线性比例,不需要任何人工定制节点的拓扑特征。
模型介绍
GraphWave 基于以该节点为中心的谱图小波的扩散,学习每个节点的结构嵌入。直观地,每个节点在图上传播能量单位,并基于网络对该探测的响应来表征其相邻拓扑。
GraphWave 使用一种新颖的方法将小波视为图上的概率分布。通过这种方式,结构信息包含在扩散如何通过网络传播而不是传播的位置。为了提供矢量值特征,然后可以将其用作任何机器学习算法的输入,GraphWave 使用经验特征函数嵌入这些小波分布。
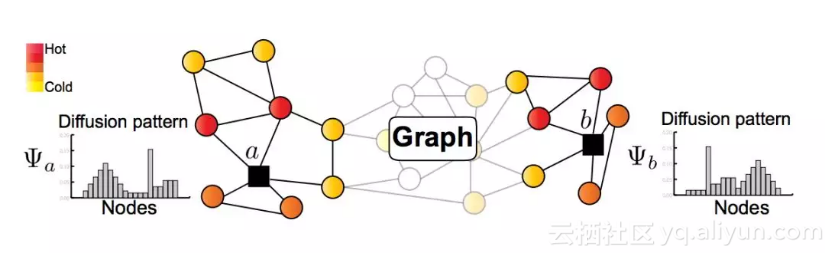
在上图中,节点 a 和 b 具有相似的局部结构角色,即使它们在图中很远。虽然 a 和 b 的原始光谱图小波签名/系数 Ψ 可能非常不同,但 GraphWave 将它们视为概率分布,因此可以自动了解系数分布确实相似。GraphWave 利用这些新见解,基于以节点 a/b 为中心的谱图小波的扩散,学习节点 a/b 的结构嵌入。

▲ GraphWave算法
实验结果
Barbell Graph
在这个例子中,文章考虑一个杠铃图,它由两个由长链连接的密集团组成。 我们将 GraphWave 应用于杠铃图并绘制学习结构签名的 2D PCA。
从下图中可以看出,该图具有 8 个不同类别的结构等效节点,如颜色(左)所示。 结构签名的 2D PCA 投影(右)包含与杠铃图中的节点相同数量的点。 这是因为相同的签名具有相同的投影,导致重叠点。
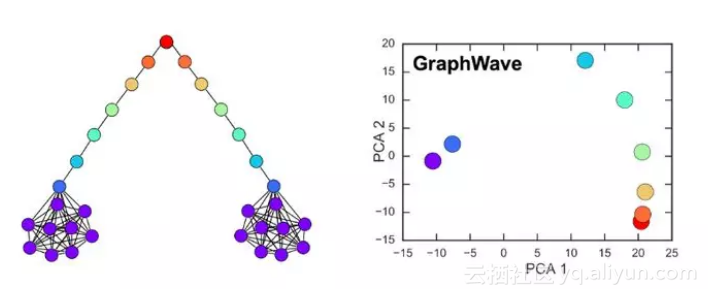
GraphWave 正确地学习了结构等效节点的相同表示,为 GraphWave 的理论保证提供了经验证据。这可以通过图中的结构等效节点(相同颜色的节点)在 PCA 图中具有相同的投影来看出。
特别是,GraphWave 正确地将 clique 节点(紫色)组合在一起。GraphWave 还正确区分连接杠铃图中两个密集团的节点。它以类似梯度的模式表示那些捕获这些节点的结构角色谱的节点(右)。
A Cycle Graph with Attached House Shapes
在这个例子中,文中考虑一个图形,其中“房屋”形状沿循环图定期放置。和以前一样,我们使用 GraphWave 来学习图中节点的结构签名,然后使用有关结构角色的地面实况信息来评估 GraphWave 的性能。
图形在下图(左)中可视化,同时还有 GraphWave 结构签名的 2D PCA 投影(中间)。我们观察到结构等效节点的表示重叠,GraphWave 完美地恢复了 6 种不同的节点类型。
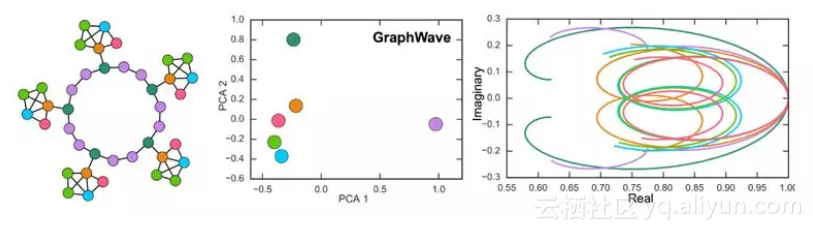
可以看到小波系数分布的最终特征函数(右)。在该图中,不同形状的特征函数捕获不同的结构角色。我们注意到这些曲线所携带的蓝色,浅绿色和红色节点的作用之间的视觉接近度,以及它们与核心深绿色和紫色节点的明显差异。
总结
本文提出了一种全新的 Network Embedding 方法 GraphWave,该方法使用谱图小波为每个节点生成结构嵌入,通过将小波视为分布并评估结果特征函数来实现,为网络嵌入提供了全新的思路。
原文发布时间为:2018-11-19
本文作者:薛寒生
本文来自云栖社区合作伙伴“PaperWeekly”,了解相关信息可以关注“PaperWeekly”。