这篇文章仅仅只是对这篇博客的总结整理,仅供自己学习之用。可能很多人会疑惑,自己转载就行了,为啥老是自己写。我觉得,不管什么东西,只有自己咀嚼过一遍,才算真的是领悟了。
1、最大似然
假设我们需要调查学校中男女生的身高分布,因为一个个的去调查费时费力,所以我们需要采用抽样的方法。假设随机抽取了100名男生和100名女生,规则是:男生在左边,女生在右边。然后先统计这100名男生的身高,假设他们的身高服从正态分布,但是这个分布的均值和方差
我们不知道,所以我们需要求这两个参数,记作
。
用数学的语言描述:在学校那么多男生的身高中,我们独立的按照概率密度(高斯分布的形式)
抽取了100个身高,组成样本集
,我们想通过样本集
估计未知参数
,而
。抽到的样本集为
,其中
表示抽到的第
个人的身高,这里
。
由于所有男生的身高服从高斯分布,那么我抽到A的概率为
,抽到B的概率为
,因为抽到每个人各自都是独立的,所以同时抽到A和B的概率为他们的乘积。所以在分布
的总体样本抽到100个样本的概率为样本集
中所有样本的联合概率:
.
这个函数说明了,在不同的参数的取值下,得到这个样本集
的可能性,因此称参数
相对于样本集
的似然函数(likehood function)。记为
。
在学校中,我抽到100个男生,他们的概率是似然函数,我们需要找到一个参数
使得似然函数最大。记为:
一般便于运算,我们将似然函数取对数,将连乘变成连加:
求最大化,然后就成立一个求导使导数为0的过程,不在赘述。所以说,最大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
2、EM算法
针对上面的例子,我们用似然函数求的男生的参数,对于女生也同样求解。但是如果例子并没有那么简单,100名男生和100名女生同在一个黑屋里,你从200个人里面随便指一个,我并不知道到底是男生还是女生。也就是说,你不知道抽取的那200个人里面的每一个人到底是从男生分布还是女生分布中取的。这个时候,对于每一个样本,就有两个东西需要猜测了。一是这个人是男是女?二是男生和女生对应的身高的高斯分布的参数是多少?。
在上面的例子中,如果没有第一个问题,那么似然函数轻松解决。但是现在有第一个问题,我们没法分析高斯分布的参数。二只有我们对这两个分布参数做了准确的估计,才知道哪些人属于第一个分布,那些人属于第二个分布。这就陷入了一个死循环。解决的方法是先对分布参数赋一个随机值,然后算出是男女的概率,然后通过男女的概率算分布参数,直到收敛。
EM的意思是“Expectation Maximization”,在我们上面这个问题里面,我们是先随便猜一下男生(身高)的正态分布的参数:如均值和方差是多少。例如男生的均值是1米7,方差是0.1米(当然了,刚开始肯定没那么准),然后计算出每个人更可能属于第一个还是第二个正态分布中的(例如,这个人的身高是1米8,那很明显,他最大可能属于男生的那个分布),这个是属于Expectation一步。有了每个人的归属,或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分,我们就可以根据之前说的最大似然那样,通过这些被大概分为男生的n个人来重新估计第一个分布的参数,女生的那个分布同样方法重新估计。这个是Maximization。然后,当我们更新了这两个分布的时候,每一个属于这两个分布的概率又变了,那么我们就再需要调整E步……如此往复,直到参数基本不再发生变化为止。
这里把每个人(样本)的完整描述看做是三元组,其中,
是第i个样本的观测值,也就是对应的这个人的身高,是可以观测到的值。
和
表示男生和女生这两个高斯分布中哪个被用来产生值
,就是说这两个值标记这个人到底是男生还是女生(的身高分布产生的)。这两个值我们是不知道的,是隐含变量。确切的说,
在
由第
个高斯分布产生时值为1,否则为0 。例如一个样本的观测值为1.8,然后他来自男生的那个高斯分布,那么我们可以将这个样本表示为{1.8, 1, 0}。如果
和
的值已知,也就是说每个人我已经标记为男生或者女生了,那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知,因此我们只能用EM算法。
3、EM算法推导
假设我们有一个样本集,包含
个独立样本。但是每个样本
对应的类别
是未知的,即隐含变量。我们需要估计概率模型
的参数
,但是里面有隐含变量
,不能用极大似然,如果
知道了,那么很容易求解。
对于参数估计,本质上还是想获得一个使似然函数最大化的那个参数,唯一不同的是似然函数式多了隐变量
。我们的目标是找到合适的
和
使得
最大,公式如下:
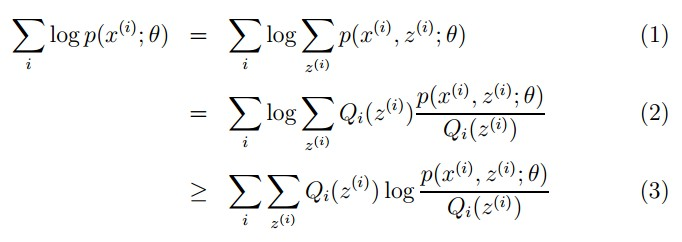
首先,我们想到是求偏导,但是很复杂,别想了。所以可以通过第(2)步变形,最后得到一个不等式,将和的对数变成对数的和。此变换是通过Jensen不等式来的。
Jensen不等式:
设是定义域为实数的函数,如果对于所有的实数
,
的二次导数大于等于0,那么
是凸函数。当
是向量,如果七hessian矩阵H是半正定的,那么
是凸函数。如果只大于0,不等于0,那么称
是严格凸函数。
Jensen不等式表述如下:
如果是凸函数,
是随机变量,那么:
。特别地,如果
是严格凸函数,当且仅当
是常量时,上式取等号。如图所示:
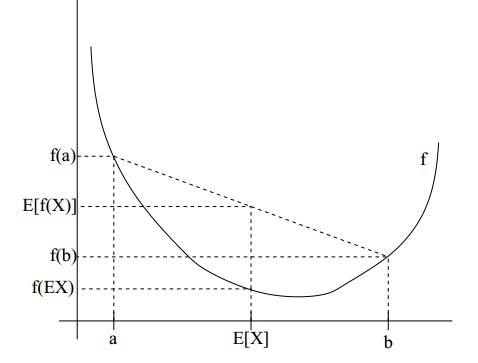
在图中,实线是凸函数,
是随机变量,有0.5概率是a,有0.5的概率是b(就像掷硬币一样)。
的期望是
和
的中值了,图中可以看到
成立。
当是(严格)凹函数,当且进度
是(严格)凸函数。
Jensen不等式应用于凹函数时,不等号方向反向。
回到公式(2),因为为凹函数(其二次导数为
)。
(2)式中,
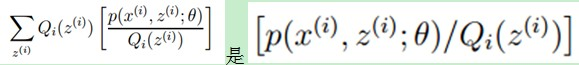
的期望,(考虑到,
是
的函数,则
),又
,所以就可以得到公式(3)的不等式了:
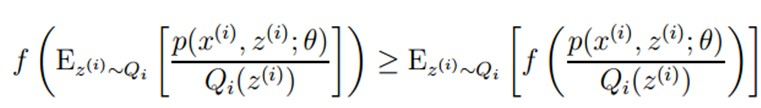
到这里,式(3)就可以很容易的求导,但是式(2)和式(3)是不等式,式(3)的最大值不是式(2)的最大值,而我们需要式(2)的最大值。
解决方法是,上面式(2)和式(3)不等式可以写成:似然函数,那么我们可以通过不断的最大化这个下界
,来使得
不断提高,最终达到它的最大值。
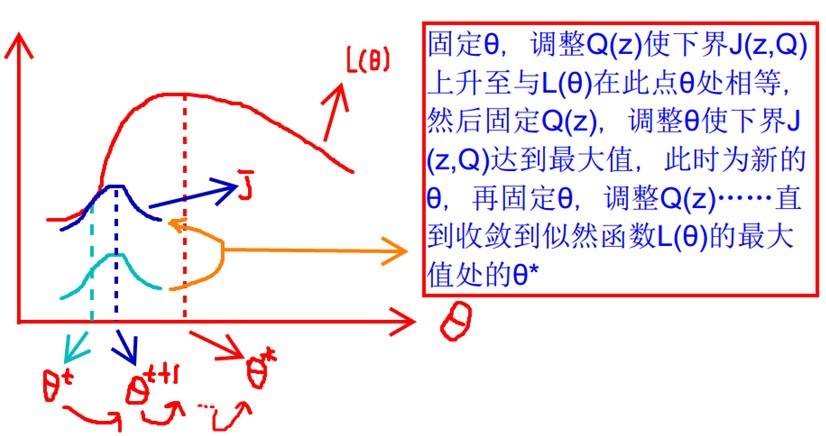
上图中,我们固定,调整
使下界
上升至与
在此点
处相等(绿色曲线到蓝色曲线),然后固定
,调整
使得下界
达到最大值(
到
),然后在固定
,调整
.....知道收敛到似然函数
的最大值处的
。两个问题:什么时候下界
与
在此点
处相等?为什么一定会收敛?
首先第一个问题,在Jensen不等式中说到,当自变量是常数的时候,等式成立。而在这里,即:
再推导下,由于(因为
是随机变量
的概率密度函数),则可以得到:分子的和等于
(分子分母都对所有
求和:多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是
),则:
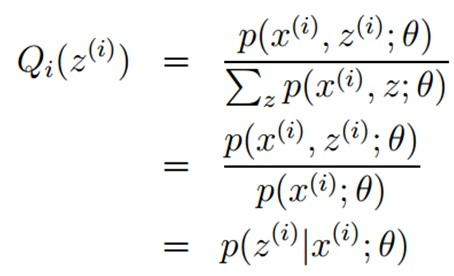
我们推出了在固定参数后,使下界拉升的
的计算公式就是后验概率,解决了
如何选择的问题。这一步就是
步,建立
的下界。接下来的
步,就是在给定
后,调整
,去极大化
的下界
(在固定
后,下界还可以调整的更大)。那么一般的EM算法的步骤如下:

4、EM算法的应用
EM算法有很多的应用,最广泛的就是GMM混合高斯模型、聚类、HMM等等,自己去搜吧。。。
最后,感谢这些大牛将这么好的文章po到网上。


