数据结构（二）：二叉搜索树（Binary Search Tree）-阿里云开发者社区

img_afd0bfa6b3945d08d04066ac0f432f0d.jpe

二分法猜数字的游戏应该每个人都知道，通过对猜测数字“大了”、“小了”的情况判断，来猜出最终的数字。序列范围为 $n$ 的集合，复杂度为 $O(log_2 n)$ ，即最多需要 $log_2 n$ 次可以猜到最终数字。

引子

二分法的查找过程是，在一个有序的序列中，每次都会选择有效范围中间位置的元素作判断，即每次判断后，都可以排除近一半的元素，直到查找到目标元素或返回不存在，所以 $n$ 个有序元素构成的序列，查找的时间复杂度为 $O(log_2 n)$ 。既然线性结构能够做到查询复杂度为 $O(log_2 n)$ 级别，那二叉搜索树产生又有何必要呢？毕竟二叉搜索树的查询复杂度只是介于 $O(log_2 n)$ ~ $O(n)$ 之间，并不存在查询优势。

定义

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：

若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

示例：

BST

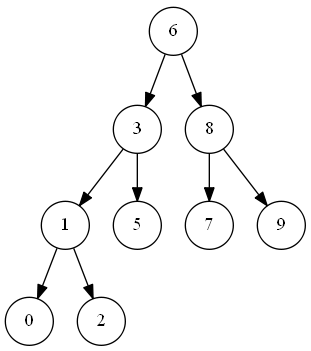
查询复杂度

观察二叉搜索树结构可知，查询每个节点需要的比较次数为节点深度加一。如深度为 0，节点值为 “6” 的根节点，只需要一次比较即可；深度为 1，节点值为 “3” 的节点，只需要两次比较。即二叉树节点个数确定的情况下，整颗树的高度越低，节点的查询复杂度越低。

二叉搜索树的两种极端情况：

【1】完全二叉树，所有节点尽量填满树的每一层，上一层填满后还有剩余节点的话，则由左向右尽量填满下一层。如上图BST所示，即为一颗完全二叉树；
【2】每一层只有一个节点的二叉树。如下图SP_BST所示：

SP_BST

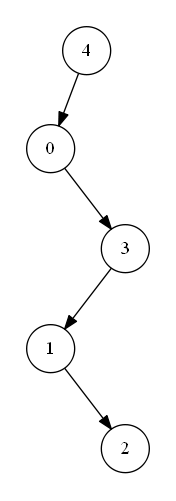
第【1】种情况下的查找次数分析：由上一章二叉树可知，完美二叉树中树的深度与节点个数的关系为： $n=2^{d+1}-1$ 。设深度为 $d$ 的完全二叉树节点总数为 $n_c$ ，因为完全二叉树中深度为 $d$ 的叶子节点层不一定填满，所以有 $n_c \le 2^{d+1}-1$ ，即： $d+1 \ge log_2{(n_c+1)}$ ，因为 $d+1$ 为查找次数，所以完全二叉树中查找次数为： $\lceil log_2{(n_c+1)} \rceil$ 。

第【2】种情况下，树中每层只有一个节点，该状态的树结构更倾向于一种线性结构，节点的查询类似于数组的遍历，查询复杂度为 $O(n)$ 。

所以二叉搜索树的查询复杂度为 $O(log_2 n)$ ~ $O(n)$ 。

构造复杂度

二叉搜索树的构造过程，也就是将节点不断插入到树中适当位置的过程。该操作过程，与查询节点元素的操作基本相同，不同之处在于：

查询节点过程是，比较元素值是否相等，相等则返回，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，返回节点不存在
插入节点的过程是，比较元素值是否相等，相等则返回，表示已存在，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，则将节点插入该空节点位置。

由此可知，单个节点的构造复杂度和查询复杂度相同，为 $O(log_2 n)$ ~ $O(n)$ 。

删除复杂度

二叉搜索树的节点删除包括两个过程，查找和删除。查询的过程和查询复杂度已知，这里说明一下删除节点的过程。

节点的删除有以下三种情况：

待删除节点度为零；
待删除节点度为一；
待删除节点度为二。

第一种情况如下图 s_1 所示，待删除节点值为 “6”，该节点无子树，删除后并不影响二叉搜索树的结构特性，可以直接删除。即二叉搜索树中待删除节点度为零时，该节点为叶子节点，可以直接删除；

s_1

s_1'

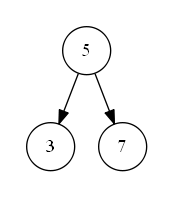
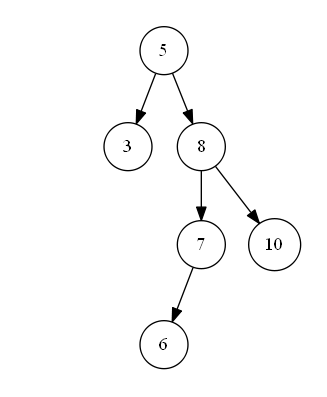
第二种情况如下图 s_2 所示，待删除节点值为 “7”，该节点有一个左子树，删除节点后，为了维持二叉搜索树结构特性，需要将左子树“上移”到删除的节点位置上。即二叉搜索树中待删除的节点度为一时，可以将待删除节点的左子树或右子树“上移”到删除节点位置上，以此来满足二叉搜索树的结构特性。

s_2

s_2'

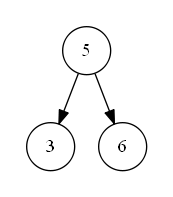
第三种情况如下图 s_3 所示，待删除节点值为 “9”，该节点既有左子树，也有右子树，删除节点后，为了维持二叉搜索树的结构特性，需要从其左子树中选出一个最大值的节点，“上移”到删除的节点位置上。即二叉搜索树中待删除节点的度为二时，可以将待删除节点的左子树中的最大值节点“移动”到删除节点位置上，以此来满足二叉搜索树的结构特性。

其实在真实的实现代码中，该情况下的实际节点删除操作是：
1.查找出左子树中的最大值节点 $Node_{max}$
2.替换待删除节点 $node$ 的值为 $Node_{max}$ 的值
3.删除 $Node_{max}$ 节点
因为 $Node_{max}$ 作为左子树的最大值节点，所以节点的度一定是 0 或 1，所以删除节点的情况就转移为以上两种情况。

s_3

s_3'

之前提到二叉搜索树中节点的删除操作，包括查询和删除两个过程，这里称删除节点后，维持二叉搜索树结构特性的操作为“稳定结构”操作，观察以上三种情况可知：

前两种情况下，删除节点后，“稳定结构”操作的复杂度都是常数级别，即整个的节点删除操作复杂度为 $O(log_2 n)$ ~ $O(n)$ ；
第三种情况下，设删除的节点为 $p$ ，“稳定结构”操作需要查找 $p$ 节点左子树中的最大值，也就是左子树中最“右”的叶子结点，即“稳定结构”操作其实也是一种内部的查询操作，所以整个的节点删除操作其实就是两个层次的查询操作，复杂度同为 $O(log_2 n)$ ~ $O(n)$ ；

性能分析

由以上查询复杂度、构造复杂度和删除复杂度的分析可知，三种操作的时间复杂度皆为 $O(log_2 n)$ ~ $O(n)$ 。下面分析线性结构的三种操作复杂度，以二分法为例：

查询复杂度，时间复杂度为 $O(log_2 n)$ ，优于二叉搜索树；
元素的插入操作包括两个步骤，查询和插入。查询的复杂度已知，插入后调整元素位置的复杂度为 $O(n)$ ，即单个元素的构造复杂度为： $O(n)$
删除操作也包括两个步骤，查询和删除，查询的复杂度已知，删除后调整元素位置的复杂度为 $O(n)$ ，即单个元素的删除复杂度为： $O(n)$

由此可知，二叉搜索树相对于线性结构，在构造复杂度和删除复杂度方面占优；在查询复杂度方面，二叉搜索树可能存在类似于斜树，每层上只有一个节点的情况，该情况下查询复杂度不占优势。

总结

二叉搜索树的节点查询、构造和删除性能，与树的高度相关，如果二叉搜索树能够更“平衡”一些，避免了树结构向线性结构的倾斜，则能够显著降低时间复杂度。二叉搜索树的存储方面，相对于线性结构只需要保存元素值，树中节点需要额外的空间保存节点之间的父子关系，所以在存储消耗上要高于线性结构。

代码附录

python版本：3.7，树中的遍历、节点插入和删除操作使用的是递归形式

树节点定义

# tree node definition
class Node(object):
    def __init__(self, value, lchild=None, rchild=None):
        self.value = value
        self.lchild = lchild
        self.rchild = rchild

树定义

# tree definition
class Tree(object):
    def __init__(self, root=None):
        self.root = root

    # node in-order traversal(LDR)
    def traversal(self):
        traversal(self.root)

    # insert node
    def insert(self, value):
        self.root = insert(self.root, value)

    # delete node
    def delete(self, value):
        self.root = delete(self.root, value)

模块中对树结构中的函数进行实现

# node in-order traversal(LDR)
def traversal(node):
    if not node:
        return
    traversal(node.lchild)
    print(node.value,end=' ')
    traversal(node.rchild)

# insert node
def insert(root, value):
    if not root:
        return Node(value)
    if value < root.value:
        root.lchild = insert(root.lchild, value)
    elif value > root.value:
        root.rchild = insert(root.rchild, value)
    return root

# delete node
def delete(root, value):
    if not root:
        return None
    if value < root.value:
        root.lchild = delete(root.lchild, value)
    elif value > root.value:
        root.rchild = delete(root.rchild, value)
    else:
        if root.lchild and root.rchild:  # degree of the node is 2
            target = root.lchild  # find the maximum node of the left subtree
            while target.rchild:
                target = target.rchild
            root = delete(root, target.value)
            root.value = target.value
        else:  # degree of the node is [0|1]
            root = root.lchild if root.lchild else root.rchild
    return root

测试代码与输出

if __name__ == '__main__':
    arr = [5, 3, 4, 0, 2, 1, 8, 6, 9, 7]
    T = Tree()
    for i in arr:
        T.insert(i)
    print('BST in-order traversal------------------')
    T.traversal()
    print('\ndelete test------------------')
    for i in arr[::-1]:
        print('after delete',i,end=',BST in-order is = ')
        T.delete(i)
        T.traversal()
        print()

输出结果为：

BST in-order traversal------------------
0 1 2 3 4 5 6 7 8 9 
delete test------------------
after delete 7,BST in-order is = 0 1 2 3 4 5 6 8 9 
after delete 9,BST in-order is = 0 1 2 3 4 5 6 8 
after delete 6,BST in-order is = 0 1 2 3 4 5 8 
after delete 8,BST in-order is = 0 1 2 3 4 5 
after delete 1,BST in-order is = 0 2 3 4 5 
after delete 2,BST in-order is = 0 3 4 5 
after delete 0,BST in-order is = 3 4 5 
after delete 4,BST in-order is = 3 5 
after delete 3,BST in-order is = 5 
after delete 5,BST in-order is =

github 链接：二叉搜索树

数据结构（二）：二叉搜索树（Binary Search Tree）

引子

定义

查询复杂度

二叉搜索树的两种极端情况：

构造复杂度

删除复杂度

节点的删除有以下三种情况：

性能分析

总结

代码附录

热门文章

最新文章

相关课程

相关电子书