数据结构（十）：最小生成树-阿里云开发者社区

img_98c13501afb7a2710dd7784e300e0162.jpe

最小生成树是带权无向连通图中权值最小的生成树，根据图中生成树定义可知， $|V|$ 个顶点的连通图中，生成树中边的个数为 $|V|-1$ ，向生成树中添加任意一条边，则会形成环。生成树存在多种，其中权值之和最小的生成树即为最小生成树。

最小生成树保证最小权值是固定的，但是最小生成树可能有多个。

若 $A$ 为最小生成树 $MST$ 的一个真子集，即 $A$ 的顶点集合和边集合都是 $MST$ 的顶点和边集合的子集，构造最小生成树过程为向 $A$ 中添加顶点和边，添加的原则有两种：

选择 $A$ 的边集合外，权值最小的边，加入到 $A$ 中

添加边的过程需要避免形成环。

选择 $A$ 的顶点集合外，距离 $A$ 最近的顶点，加入到 $A$ 中

距离 $A$ 最近的点，即和 $A$ 中的顶点形成最小权值边的非 $A$ 中的某个顶点。

kruskal 算法

kruskal 算法即为上述第一种原则，通过选择图中的最小权值边来构造最小生成树，过程中需要注意避免形成环。

算法过程

对边集合进行排序
选择最小权值边，若不构成环，则添加到集合 $A$ 中
重复执行步骤 2，直到添加 $|V|-1$ 条边

演示示例

graph

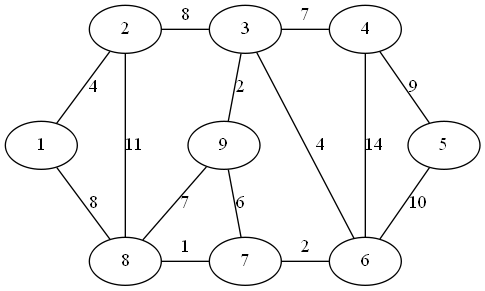
step 1：
最小权值边为顶点 7、8 形成的边

step 2：
最小权值边为顶点 3、9 形成的边

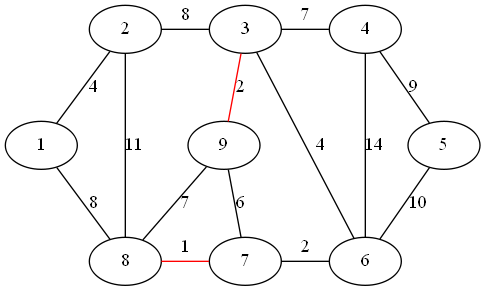
step 3：
最小权值边为顶点 6、7 形成的边

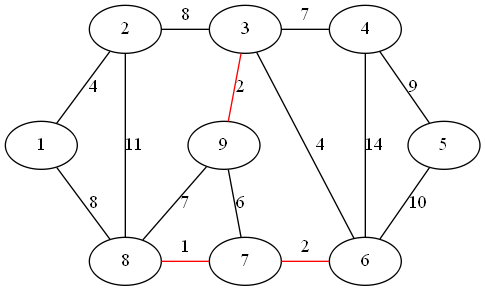
step 4：
最小权值边为顶点 3、6 形成的边

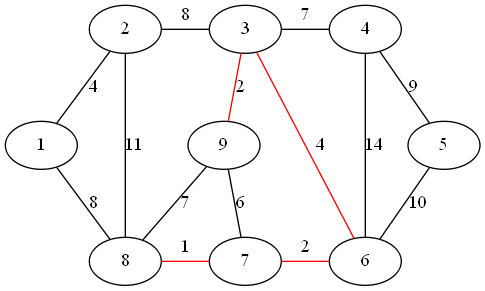
step 5：
最小权值边为顶点 1、2 形成的边

step 6：
最小权值边为顶点 3、4 形成的边

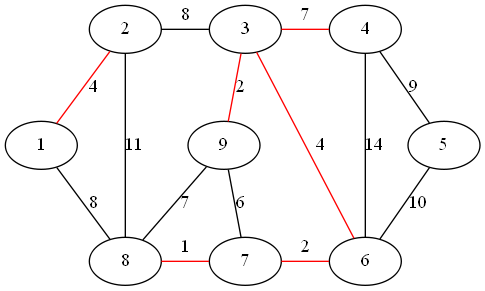
step 7：
最小权值边为顶点 1、8 形成的边

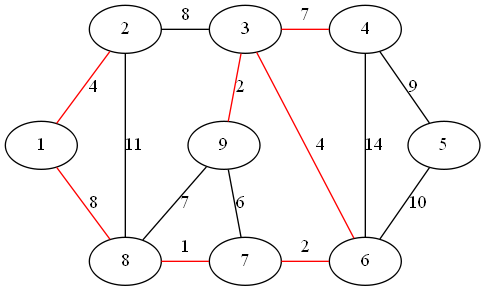
step 8：
最小权值边为顶点 4、5 形成的边

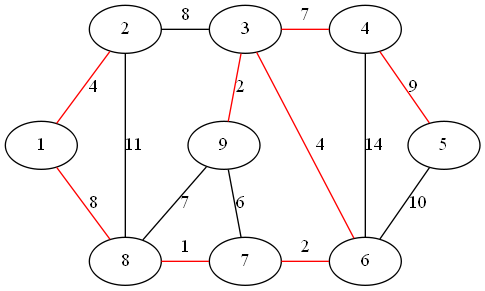
最小生成树的权值之和为 37

算法示例

这里使用邻接表作为图的存储结构

kruskal 算法示例

def kruskal(graph):
    edges, vertices = getEdgesFromAdjacencyList(graph), [i for i in range(graph.number)]
    sort(edges, 0, len(edges) - 1)
    weightSum, edgeNumber = 0, 0
    while edgeNumber < graph.number - 1:
        edge = edges.pop()
        beginOrigin, endOrigin = origin(vertices, edge.begin - 1), origin(vertices, edge.end - 1)
        if (beginOrigin != endOrigin): # whether the two vertices belong to same graph
            vertices[beginOrigin] = endOrigin  # identify the two vertices in the same sub graph
            weightSum, edgeNumber = weightSum + edge.weight, edgeNumber + 1  # calculate the total weight

这里使用 getEdgesFromAdjacencyList 函数完成邻接表到边集合的转换，使用快排 sort 完成对边集合的排序，使用 origin 函数返回每个子图的根。

kruskal 算法设定最初每个顶点都是一个子图，每个子图都有一个根，或者称之为出发点，每个加入的顶点都保留一个指向上一个顶点的引用，并最终追溯到该子图的根顶点，所以可以通过判断两个顶点指向的根顶点是否相同，来判断两顶点是否属于同一个子图。

邻接表转边集合

def getEdgesFromAdjacencyList(graph):
    edges = []
    for i in range(graph.number):
        node = graph.list[i]
        while node:
            edge, node = Edge(i + 1, node.index, node.weight), node.next
            edges.append(edge)
    return edges

因为使用邻接表向边进行转化，且后续只对边集合进行处理，所以在测试时候，无向图中的每条边，只需要记录一次即可，不需要对于边的两个顶点，分别记录一次。

判断两个顶点是否属于同一个子图，避免添加边后形成环

def origin(vertices, index):
    while vertices[index] != index:
        index = vertices[index]
    return index

该函数返回顶点 index 所属子图的根顶点，其中 vertices[index] 位置上存储的是顶点 index 的上一个顶点，每个子图中，根顶点的上一个顶点为自身。

性能分析

kruskal 算法中使用 getEdgesFromAdjacencyList 函数完成邻接表向边集合的转换，函数内部存在两层循环，访问邻接表中每个顶点的相邻顶点，复杂度为 $O(log|E|)$ 。使用快排对边集合进行排序，时间复杂度为 $O(|E|log |E|)$ ，因为 $|E| \lt |V|^2$ ，所以快排时间复杂度可以表述为 $O(|E|log |V|)$ 。kruskal 算法中 while 循环取最小权值边，并对边的两个顶点执行 origin 函数判断是否属于同一个子图，时间复杂度为 $O(|E|log |V|)$ 。所以 kruskal 算法的时间复杂度为 $O(|E|log |V|)$ 。

prim 算法

kruskal 算法的过程为不断对子图进行合并，直到形成最终的最小生成树。prim 算法的过程则是只存在一个子图，不断选择顶点加入到该子图中，即通过对子图进行扩张，直到形成最终的最小生成树。

扩张过程中选择的顶点，是距离子图最近的顶点，即与子图中顶点形成的边是权值最小的边。

算法过程

按照距离子图的远近，对顶点集合进行排序
选择最近的顶点加入到子图中，并更新相邻顶点对子图的距离
重复执行步骤 2，直到顶点集合为空

演示示例

graph

这里不妨以顶点 5 作为子图中的第一个顶点

step 1：
距离子图的最近顶点为 4

step 2：
距离子图的最近顶点为 3

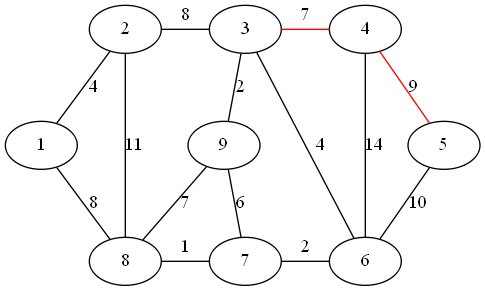
step 3：
距离子图的最近顶点为 9

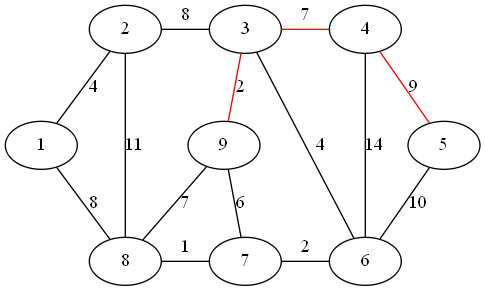
step 4：
距离子图的最近顶点为 6

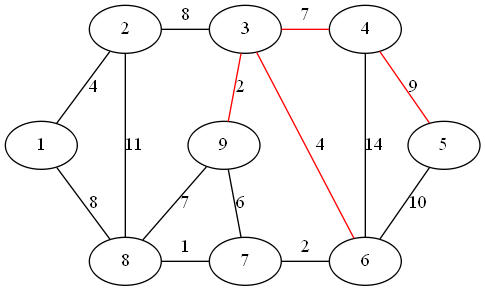
step 5：
距离子图的最近顶点为 7

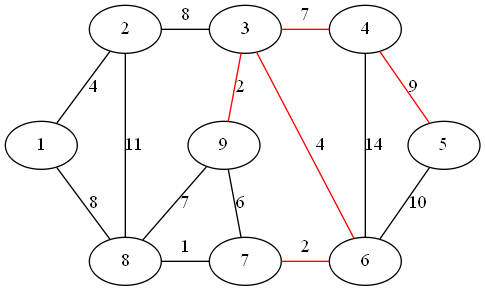
step 6：
距离子图的最近顶点为 8

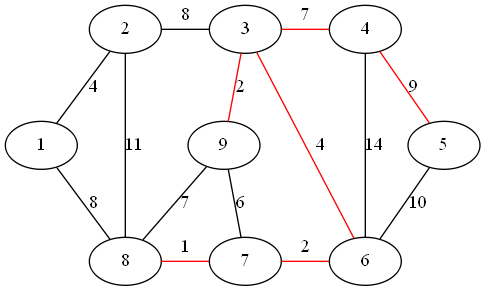
step 7：
距离子图的最近顶点为 2

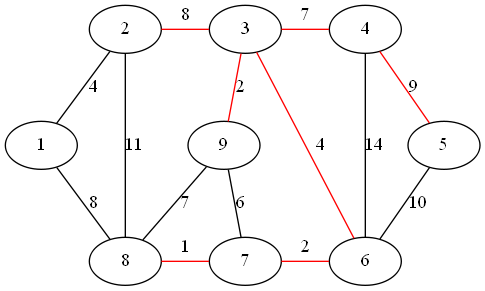
step 8：
距离子图的最近顶点为 1

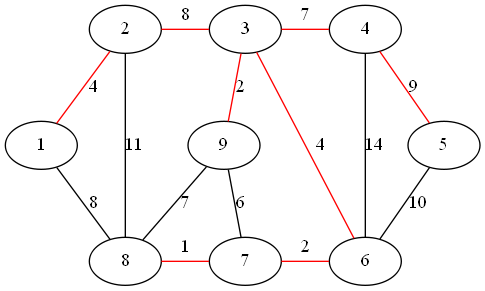
最小生成树的权值之和为 37

算法示例

这里使用邻接表作为图的存储结构

prim 算法示例

def prim(graph, index):
    vertices, verticesIndex = [{'index': i, 'weight': None} for i in range(graph.number)], [i for i in range(graph.number)]
    weightSum, vertices[index - 1]['weight'] = 0, 0
    heapSort(vertices, verticesIndex)
    while len(vertices) > 0:
        swapVertices(vertices, verticesIndex, 0, -1)
        vertex = vertices.pop()
        transformToHeap(vertices, verticesIndex, 0, len(vertices))
        weightSum = weightSum + vertex['weight']
        updateVertices(graph, vertices, verticesIndex, vertex['index'])

这里使用 vertices 列表存储每个顶点元素，每个元素包括两个属性，index 为顶点下标，weight 为顶点距离子图的大小。算法中使用 verticesIndex 列表存储每个顶点元素在 vertices 列表中的下标位置。使用 heapSort 堆排序对每个顶点到子图的距离进行排序，即对 vertices 列表进行排序，使用堆排序内的 transformToHeap 函数调整 vertices 列表为小顶堆。当添加新顶点到子图后，使用 updateVertices 函数完成对相邻顶点的距离更新。

因为对 vertices 列表排序后，每个顶点元素在 vertices 列表的下标值不能表示该顶点的编号，而后续添加新顶点后，在更新相邻顶点距离的操作中，为了避免查找相邻顶点而遍历整个列表，需要根据顶点编号进行直接访问相邻顶点，所以借助 verticesIndex 列表存储每个顶点元素在 vertices 列表中的位置。例如要更新顶点 $v$ 的距离，则 verticesIndex[v] 值为顶点 $v$ 在 vertices 列表中的位置， $v$ 顶点元素即为 vertices[verticesIndex[v]]。

交换堆顶元素

def swapVertices(vertices, verticesIndex, origin, target):
    vertices[origin], vertices[target] = vertices[target], vertices[origin]
    verticesIndex[vertices[origin]['index']], verticesIndex[vertices[target]['index']] = origin, target

当 vertices 列表调整为小顶堆之后，将列表首、尾元素交换，则列表尾元素即为距离子图最近的顶点元素。

添加顶点到子图中后，更新相邻顶点到子图的距离

def updateVertices(graph, vertices, verticesIndex, index):
    node = graph.list[index]
    while node:
        if verticesIndex[node.index - 1] == -1:
            node = node.next
            continue
        vertex = vertices[verticesIndex[node.index - 1]]
        if not vertex['weight'] or (vertex['weight'] and vertex['weight'] > node.weight):
            vertex['weight'] = node.weight
            pos = verticesIndex[vertex['index']]
            while pos > 0 and (not vertices[(pos - 1) // 2]['weight'] or vertices[pos]['weight'] < vertices[(pos - 1) // 2]['weight']):
                swapVertices(vertices, verticesIndex, pos, (pos - 1) // 2)
                pos = (pos - 1) // 2
        node = node.next

对每一个相邻顶点，如果不在子图中，则判断是否更新到子图的距离。

性能分析

prim 算法中构造顶点列表的时间复杂度为 $O(|V|)$ 。使用堆排序对顶点列表进行排序，时间复杂度为 $O(|V|log |V|)$ 。prim 算法中 while 循环取最近顶点元素，并调整元素取出后列表的堆结构，所以总体的调整复杂度为 $O(|V|log |V|)$ ；同时循环结构内执行 updateVertices 函数，更新每个取出顶点的相邻顶点距离值，所以总体的更新顶点数为 $O(|E|)$ ，因为每个顶点更新距离后，需要调整堆结构为小顶堆，所以总体的复杂度为 $O(|E|log |V|)$ 。所以prim 算法的时间复杂度为 $O(|E|log |V|)$ 。