数据科学,不管它到底是什么,其影响力已不可忽视。“数据科学家比任何软件工程师都更擅长统计学。”你可能在本地的技术聚会或者黑客松上无意中听到一个专家这么说。应用数学家大仇得报,毕竟从咆哮的二十年代起人们就不怎么谈论统计学了。以前聊天的时候,像你这样的工程师,会因为分析师从来没听说过Apache Bikeshed(口水仗)这个分布式评论格式编排项目而发出啧啧声。现在,你却突然发现人们在聊置信区间的时候不带上你了。为了融入聊天,为了重新成为聚会的灵魂人物,你需要恶补下统计学。不用学到正确理解的程度,只需学到让人们(基于基本的观测)觉得你可能理解了的程度。
正如数据结构是计算机科学的基础,概率分布是统计学的基础。如果你计划像一个数据科学家一样聊天,那么概率分布就是你学习的起点。有时候,不怎么理解概率分布的情况下,使用R或scikit-learn就可以完成一些简单的分析,就像不理解哈希函数也可以编写Java程序一样。然而,很快你就会碰到bug和虚假的结果,并为此痛哭流涕,或者更糟:收获统计学专业人士的叹息和白眼。
概率分布有数百种,有些听起来像是中世纪传说中的怪兽,比如Muth和Lomax。不过,实践中经常出现的概率分布只有15种。这15种概率分布是什么?关于它们你需要记忆哪些明智的洞见?请看下文。
什么是概率分布?
每时每刻都有各种事件正在发生:骰子掷出、雨滴落下、巴士到站。事件发生之后,特定的结果便确定了:掷出3点加4点,今日的降雨量是半英寸,巴士3分钟到站。在事件发生之前,我们只能讨论结果的可能性。概率分布描述我们对每种结果出现概率的想法,有些时候,我们更关心概率分布,而不是最可能出现的单个结果。概率分布有各种形状,但大小只有一种:概率分布的概率之和恒等于1.
例如,抛掷一枚匀质硬币有两种结果:正面、反面。(假定硬币落地时不可能以边缘立起,或者被空中的海鸥偷走。)在扔硬币之前,我们相信有二分之一的几率扔到正面,或者说,0.5的概率。扔到反面的概率同理。这是扔硬币的两种结果的概率分布。实际上,如果你充分理解了上面的话,那么你已经掌握了伯努利分布。
除了奇异的名字之外,常见分布之间的关系直观而有趣,所以不管是记忆它们,还是以权威的语气评论它们,都很容易。例如,不少分布都能很自然地从伯努利分布导出。是时候揭开概率分布的相互关系地图了。
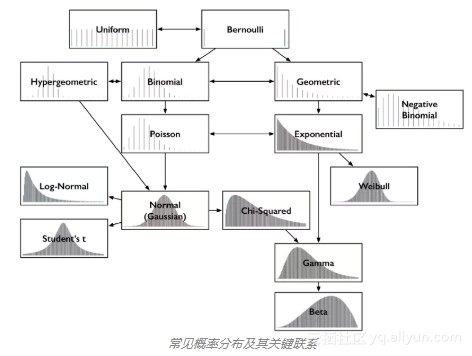
上图中的每种分布都包含相应的概率质量函数或概率密度函数。本文只涉及结果为单个数字的分布,所以横轴均为可能的数值结果的集合。纵轴描述了结果概率。有些分布是离散的,例如,结果为0到5之间的整数,其概率质量函数图形为稀疏的直线,每根线表示一种结果,线高表示该结果的概率。有些分布是连续的,例如,结果为-1.32到0.005之间的任意实数,其概率密度函数为曲线,曲线下的面积表示概率。概率质量函数的线高之和,概率密度函数的曲线下面积,总是等于1.
把上面这张图打印出来放到钱包或坤包中。它能指引你厘清概率分布和它们之间的联系。
伯努利分布和均匀分布
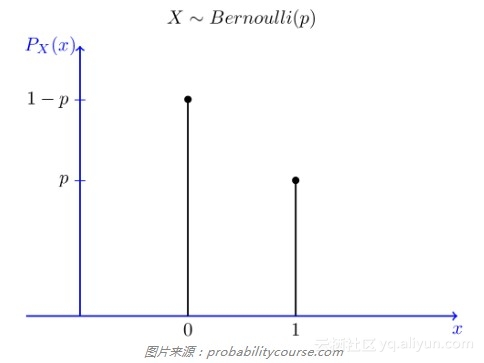
你已经通过上面扔硬币的例子接触过伯努利分布了。扔硬币有两个离散的结果——正面或反面。不过,你可以把结果看成0(反面)或1(正面)。这两种结果发生的可能性都一样,如下图所示。
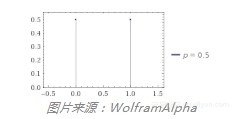
伯努利分布可以表示可能性不同的结果,例如抛掷一枚不均匀的硬币。那么,扔到正面的概率就不是0.5,而是不等于0.5的概率p,扔到反面的概率则是1-p. 和很多分布一样,伯努利分布实际上是由参数定义的一系列分布(伯努利分布由p定义)。你可以将“伯努利”想象为“扔(可能不均匀的)硬币”。
有多个结果,所有结果发生概率相等的分布,则是均匀分布。想象抛掷一枚匀质骰子,结果为1点到6点,出现每种点数的可能性相同。均匀分布可以由任意数目n的结果定义,甚至可以是连续分布。
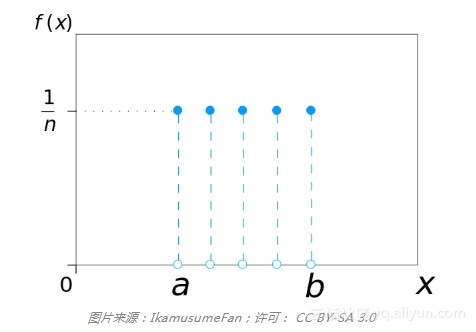
看到均匀分布,就联想“投掷一枚均质骰子”。
二项分布和超几何分布
二项分布可以看成遵循伯努利分布的事件的结果之和。抛掷一枚均质硬币,扔20次,有多少次扔出正面?这一计数的结果遵循二项分布。它的参数是试验数n和“成功”(这里的“成功”指正面,或1)的概率p。每次抛掷硬币得到的是一个遵循伯努利分布的结果,也就是一次伯努利试验。累计类似抛掷硬币(每次抛掷硬币的结果相互独立,成功的概率保持不变)的事件的成功次数时,想想二项分布。
或者,你可以想像一个瓮,其中放着数量相等的白球和黑球。闭上你的眼睛,从瓮里抽一个球,并记录它是不是黑球,接着把这个球放回。重复这一过程。你有多少次抽到黑球?这一计数同样遵循二项分布。
想象这种奇怪的场景是有意义的,因为这让我们容易解释超几何分布。在上面的场景中,如果我们不放回抽取的球,那么结果计数就遵循超几何分布。毫无疑问,超几何分布是二项分布的表兄弟,但两者并不一样,因为移除球后成功的概率改变了。如果球的总数相对抽取数很大,那么这两个分布是类似的,因为随着每次抽取,成功的几率改变很小。
当人们谈论从瓮中抽取球而没有提到放回时,插上一句“是的,超几何分布”几乎总是安全的,因为我在现实生活中从来没碰到任何人真用球装满一个瓮,接着从中抽球,然后放回。(我甚至不知道谁拥有一个瓮。)更宽泛的例子,是从种群中抽取显著的子集作为样本。
泊松分布
累计每分钟呼叫热线的客户数?这听起来像是二项分布,如果你把每一秒看成一次伯努利试验的话。然而,电力公司知道,停电的时候,同一秒可能有数百客户呼叫。将它看成60000次毫秒级试验仍然不能解决这个问题——分割的试验数越多,发生1次呼叫的概率就越低,更别说2次或更多呼叫了,但是这个概率再低,技术上说,始终不是伯努利试验。然而,如果n趋向于无限,p趋向于0,相当于在无穷多个无穷小的时间切片上,呼叫概率无穷小,我们就得到了二项分布的极限,泊松分布。
类似二项分布,泊松分布是计数的分布——某事件发生的计数。泊松分布的参数不是概率p和试验次数n,而是平均发生率λ(相当于np)。试图累计连续事件发生率,统计一段时间内某事件的发生数时,千万别忘了考虑泊松分布。
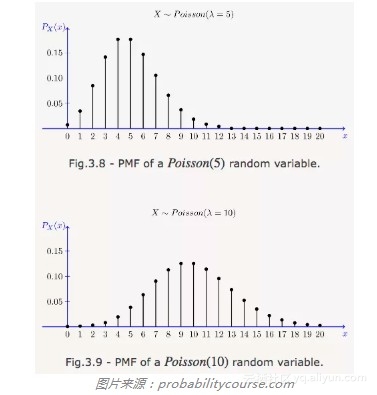
到达路由的包、到访商店的客户、在某种队列中等待的事物,遇到类似这样的事情,想想“泊松”。
几何分布和负二项分布
从伯努利试验又可以引出另一种分布。在第一次出现正面向上之前,扔出了多少次背面向上的硬币?这一计数遵循几何分布。类似伯努利分布,几何分布由参数p(成功概率)决定。几何分布的参数不包括试验数n,因为结果本身是失败的试验数。
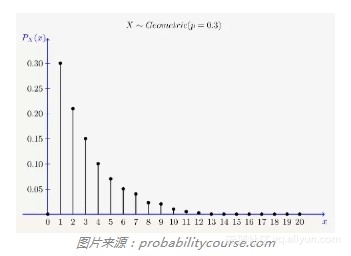
如果说伯努利分布是“成功了多少次”,那么几何分布就是“在成功前失败了多少次”。
负二项分布是几何分布的简单推广。它是成功r次前失败的次数。因此,负二项分布有一个额外的参数,r。有时候,负二项式分布指r次失败前成功的次数。我的人生导师告诉我,成功和失败取决于你的定义,所以这两种定义是等价的(前提是概率p与定义保持一致)。
聊天时,如果你想活跃气氛,那么可以说,显然,二项分布和超几何分布是一对,但是几何分布和负二项分布也很类似,接着提问:“我想说,谁起名字起得这么乱?”
指数分布和威布尔分布
回到客户支持电话的例子:距下一个客户呼叫还有多久?这一等待时间的分布听起来像几何分布,因为直到终于有客户呼叫的那一秒为止,无人呼叫的每一秒可以看成失败。失败数可以视为无人呼叫的秒数,这几乎是下一次呼叫的等待时间,但还不够接近。这次的问题在于,这样计算出的等待时间总是以整秒为单位,没有计入客户最终呼叫的那一秒中的等待时间。
和之前一样,对几何分布取极限,趋向无穷小的时间切片,可以奏效。我们得到了指数分布。指数分布精确地描述了下一呼叫前的时间分布。它是一个连续分布,因为结果不一定是整秒。类似泊松分布,指数分布由参数发生率λ决定。
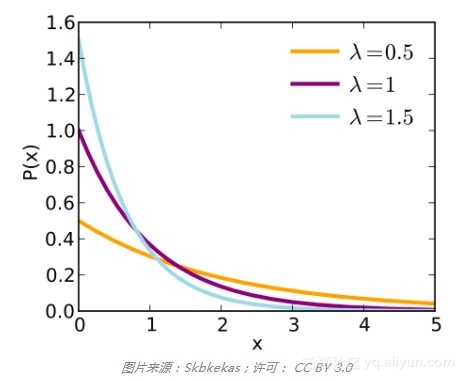
和二项分布与几何分布之间的关系相呼应,泊松分布是“给定时间内事件发生了多少次”,指数分布则是“直到事件发生过了多少时间”。给定一个某段时间内发生次数遵循泊松分布的事件,那么事件间隔时间遵循参数λ相同的指数分布。正是基于这两种分布之间的这一对应关系,在谈论两者之一时提下另一种是很安全的。
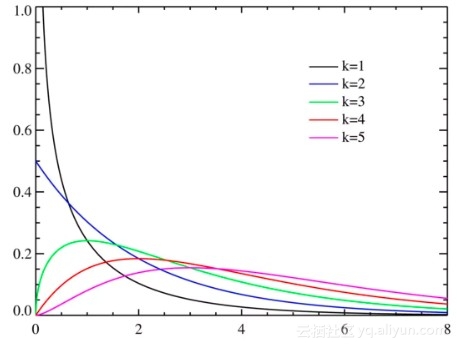
涉及“到某事件发生前的时间”(也许是“无故障工作时间”),应该考虑指数分布。实际上,无故障工作时间是如此重要,我们有一种更一般的分布对其加以描述,威布尔分布。指数分布适用于发生率(例如,损毁或故障概率)恒定的情况,威布尔分布则可以建模随着时间而增加(或减少)的发生率。指数分布不过是威布尔分布的一个特例。
当聊天转向无故障工作时间时,考虑“威布尔”。
正态分布、对数正态分布、t分布、卡方分布
正态分布,又称高斯分布,也许是最重要的概率分布。它的钟形曲线极具辨识度。像自然对数e一样,神奇的正态分布随处可见。从同一分布大量取样——任何分布——然后相加,样本的和遵循(近似的)正态分布。取样数越大,样本之和就约接近正态分布。(警告:必须是非病态分布,必须是独立分布,仅仅趋向正态分布)。无论原分布是何种分布,这一点均成立,真是令人惊奇。
这称为中心极限定理,你必须知道这个名词和它的含义,不然立遭哄笑。
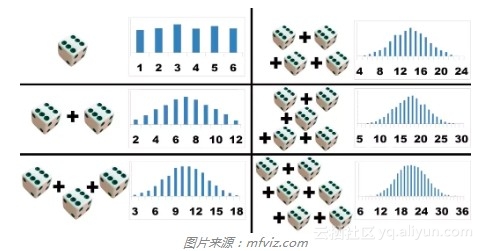
从这个意义上说,正态分布和所有分布相关。不过,正态分布和累加尤为相关。伯努利实验的和遵循二项分布,随着试验数的增加,二项分布变得越来越接近正态分布。它的表兄弟超几何分布也是一样。泊松分布——二项分布的极端形式——也随着发生率参数的增加而逼近正态分布。
如果对结果取对数,所得遵循正态分布,那么我们就说结果遵循对数正态分布。换句话说,正态分布值的对数遵循对数正态分布。如果和遵循正态分布,那么相应的乘积遵循对数正态分布。
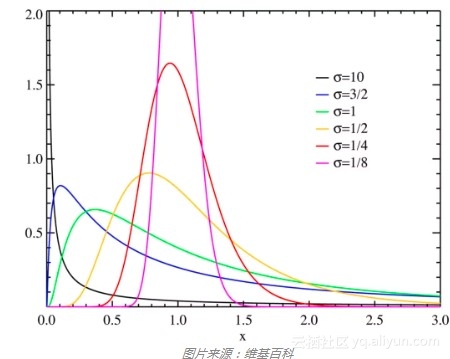
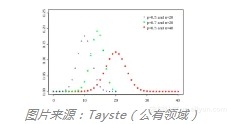
学生t-分布是t检验的基础,许多非统计学家在其他学科中接触过t检验。它用于推断正态分布的均值,随着其参数的增加而更加接近正态分布。学生t-分布的主要特点是,尾部比正态分布更厚(见下图所示,红线为学生t-分布,蓝线为标准正态分布)。
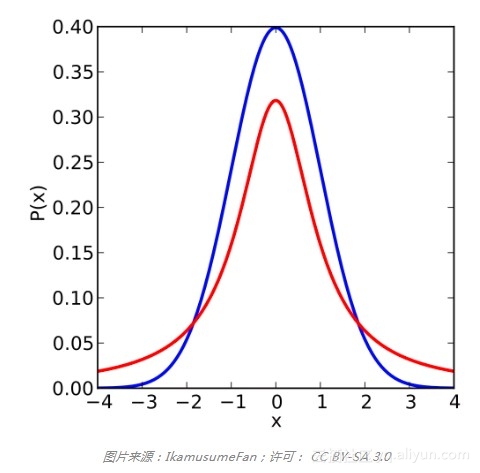
如果厚尾的说法不能引起邻居的惊叹,那可以讲讲比较有趣的和啤酒有关的背景故事。一百年前,Guinness使用统计学酿制更好的烈性黑啤酒。在Guinness,William Sealy Gosset研究出了一种新的统计学理论以种出更好的大麦。Gosset说服老板其他酿酒商无法搞明白如何利用这些想法,取得了发表成果的许可,不过是以笔名“学生”发表。Gosset最出名的成果就是学生t-分布,某种程度上而言是以他的名字命名的。
最后,卡方分布是正态分布值的平方和的分布。它是卡方检验的基础。卡方检验基于观测值和理论值的差(假定差遵循正态分布)的平方和。
伽玛分布和贝塔分布
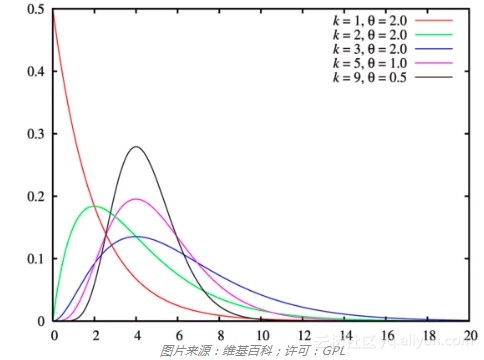
如果都谈到卡方分布之类了,那么谈话应该算是比较严肃的。你可能在和真正的统计学家聊天,到了这个份上,你也许该致歉,表示自己知道的不多,因为伽玛分布之类的名词会出现了。伽玛分布是指数分布和卡方分布的推广。伽玛分布通常用作等待时间的复杂模型,这一点上更像指数分布。例如,伽玛分布可以用来建模接下来第n个事件发生前的时间。在机器学习中,伽玛分布是一些分布的“共轭先验”。
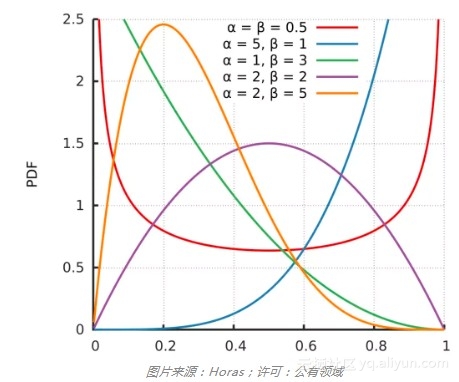
别在共轭先验的对话中插话,不过如果你真的插话了,准备好谈论贝塔分布,因为它是上面提到过的大多数分布的共轭先验。就数据科学家而言,贝塔分布的用途主要在此。不经意地提到这一点,然后朝门口移动。
智慧的开端
概率分布的知识浩如烟海。真正对概率分布感兴趣的可以从下面这张所有单元分布的地图开始。
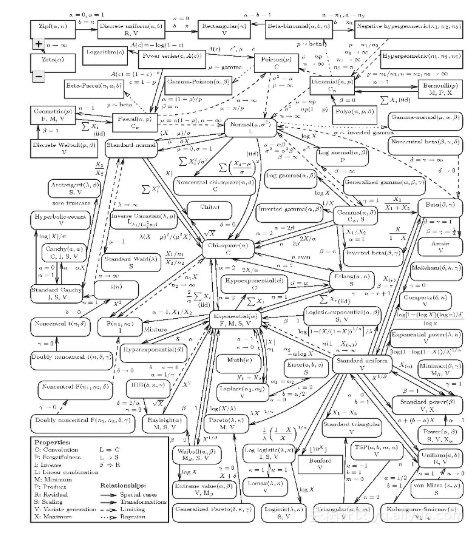
希望本文能给你一点信心,让自己看起来知识渊博,并且能融入今日的技术文化。或者,至少能为你提供一种方法,能够以很高的概率判断什么时候你应该找一个不那么书呆的鸡尾酒会。
原文发布时间为:2018-10-25
本文作者:weakish
本文来自云栖社区合作伙伴“深度学习自然语言处理”,了解相关信息可以关注“深度学习自然语言处理”。