上一篇文章介绍了MDP的基本概念,但是我们更关心的是如何寻找到最佳的路径解决MDP问题。MDP过程中,可以有无数种策略(policy),找到最佳的路径实际上就是找到最佳的Policy 来最大化V函数(Value Function)或者Q函数(Action-Value Function)。
用数学表达式表达出来就是:
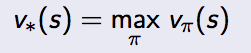
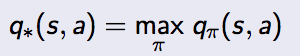
其中加星号* 的v和q表示最优的v和q。
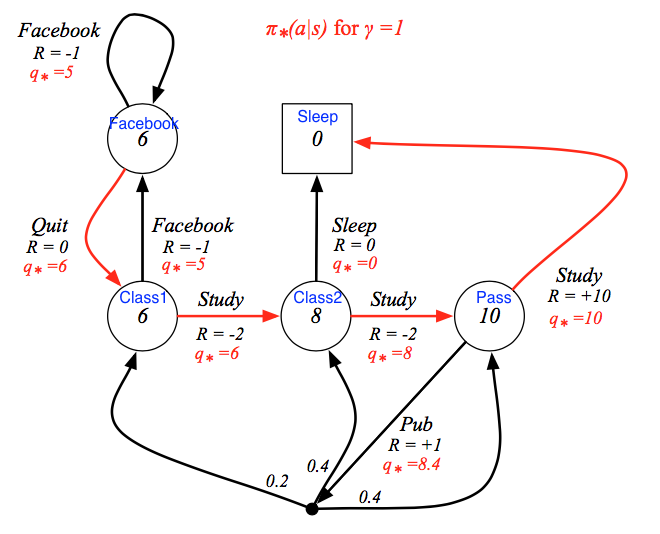
还记得上一篇文章中的那个例子吗?学生学习的的状态有Facebook, Class1, Class2, Pass, Sleep 6个状态(State),每个状态都有一个或者多个行动(Action)。最优的V函数和Q函数都已求出来了,找到最优策略就是找到最大q*的过程。显然红色的路径就是最优策略,只有沿着这条路径才能的到最大的奖励。
同样的,用Bellman 等式可以得到最优V函数和最优Q函数的关系,以及他们自己的递归关系:
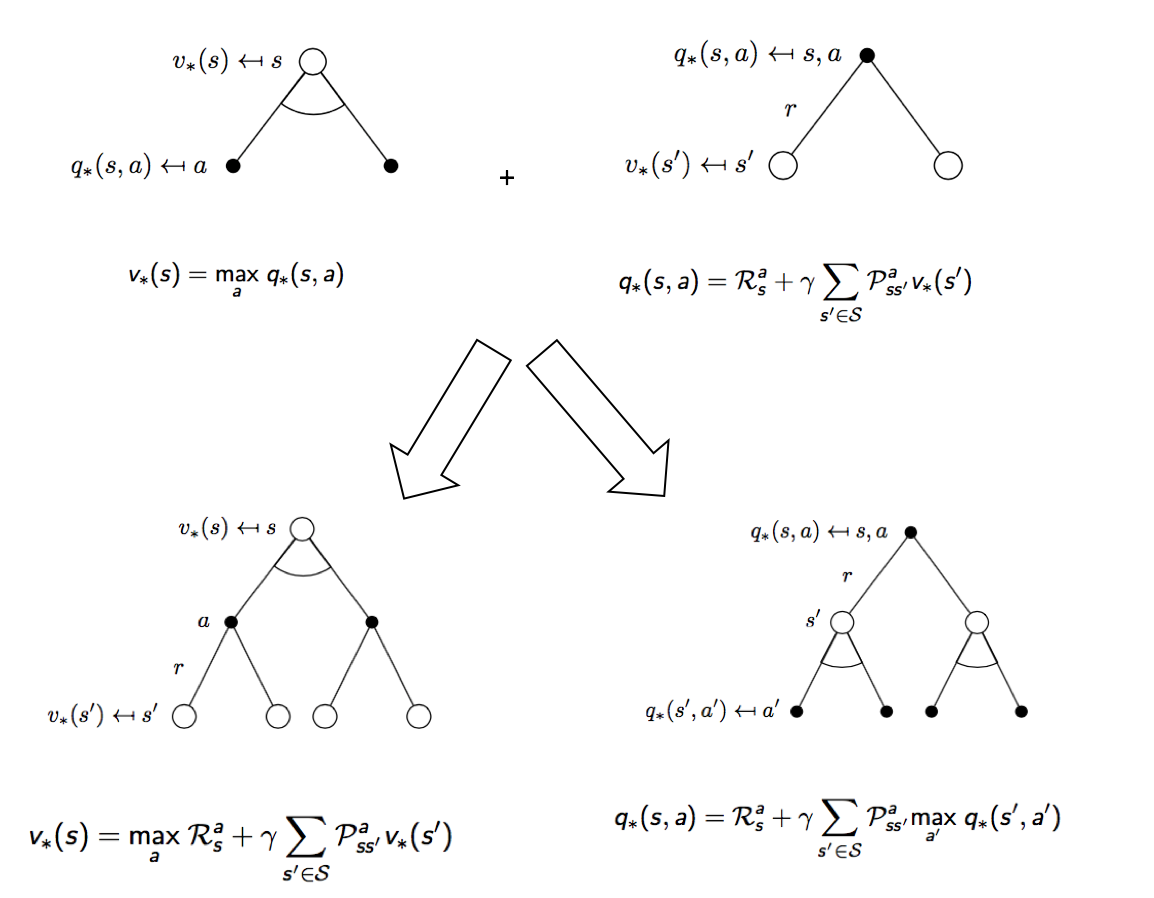
同样的用Bellman等式,我们可以验证为什么V(Pass) = 10.
Pass 这个状态有两个行动,分别为Study和Pub。Study 对应一个状态Sleep,Pub对应三个状态Class1, Class2, 和 Pass。那么假设γ=1
V(Pass) = Max{+10+0,+1+(0.2x6 + 0.48 + 0.410)} = Max{10, 8.6} = 10。
用同样的方法可以验证每一个状态的V函数。
当然我们现在只能验证,无法真正求解最优V函数和Q函数,如果能求解最优Ballman 等式我们就能得到最优的V函数和Q函数进而得到最优的策略。
但是遗憾的是最优Ballman等式并不是线性的,所以不能直接通过解线性方程的方法求得。但是可以通过一些迭代算法求得,之前的Q-Learning和Sarsa 算法就是求最优Ballman等式的算法,当然这些算法也就是强化学习的算法了。
文章首发steemit.com 为了方便墙内阅读,搬运至此,欢迎留言或者访问我的Steemit主页