日常管理,先上思维导图
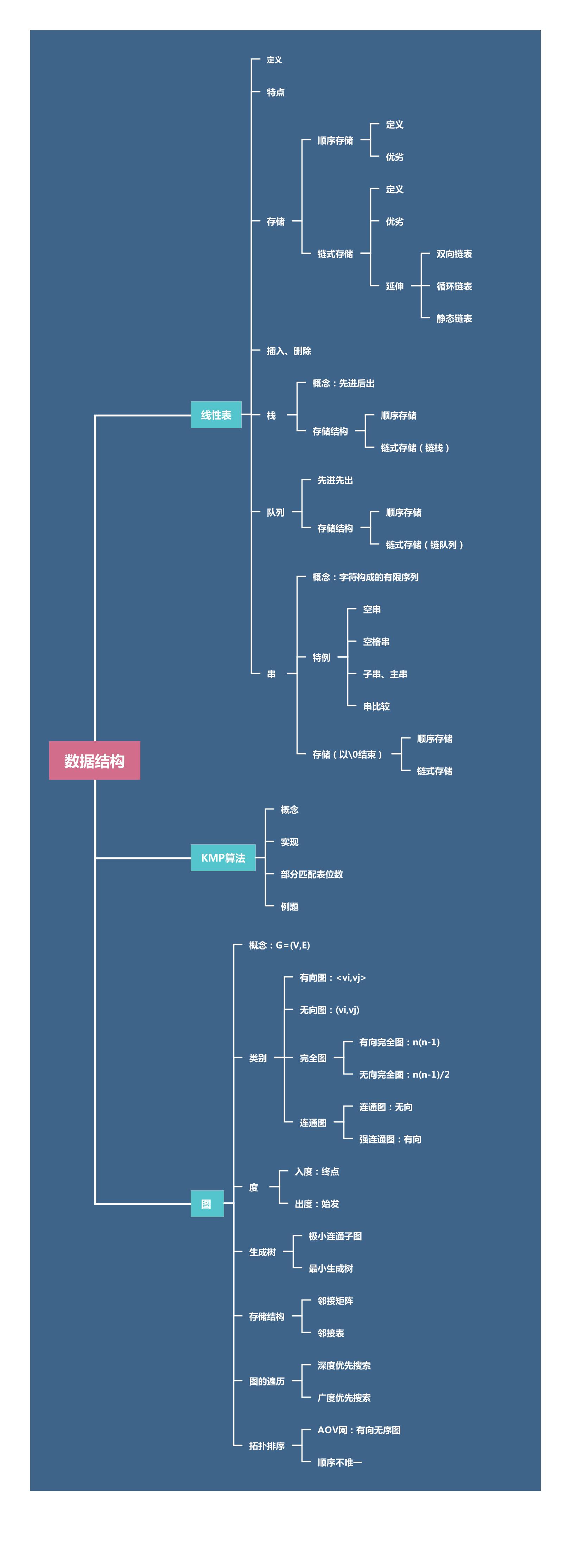
线性表
1 定义:n个元素的有限序列,通常记为(a1,a2,...,an)
2 特点:存在唯一表头表尾,直接前驱,直接后继
3 存储
1)顺序存储
定义:用一组地址连续的存储单元依次存储线性表中的数据元素,逻辑、物理紧邻,类似数组
优劣:可随机存取元素,但修/删需要移动大量元素
2)链式存储
定义:用结点来存储数据元素,逻辑紧邻,物理(不)连续
优劣:插/删不需移动元素,但增加了存储开销,不能随机访问结点(保存数据域和指针域)
延伸:1)双向链表:每个结点包含两个指针,指明直接前驱和直接后继元素,可在两个方向上遍历链表

2)循环链表:表尾结点的指针指向表头结点,可在任何位置遍历整个元素

3)静态链表:借助数组来描述线性表的连接存储方式
4 线性表的插入和删除
1)顺序存储结构
挪元素,插入;删元素,挪动
2)链式存储结构
实质:对相关指针的修改
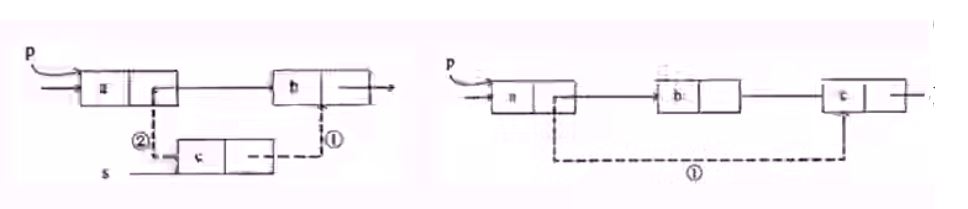
插入:先读取P指针next指向,即b地址;
让C指向它;
然后让P指向C的地址;
删除:a指向被删除元素(b)指向的元素c
栈
1 概念:通过一端(栈顶)实现数据存储和检索的一种线性表,有栈底,先进后出
2 存储结构
1)顺序存储
增加指针top指向栈顶元素
2)链式存储(链栈)
不必设头节点(栈顶操作),头指针=栈顶指针
队列
1 概念:先进先出的线性表,一端插入(对尾),另一端删除(对头)
2 存储结构
1)顺序存储
设置队头/尾两个指针
2)链式存储(链队列)
添加头结点,指向头指针。
队列为空,头指针=尾指针,指向头节点
串
1 概念:由字符构成的有限序列,取值范围受限的线性表。记为S=’a1 a2 a3 ... an‘,S是串名,右边是串值
2 特例:1)空串:长度为零 的串,,无任何字符
2)空格串:一/多个空格串构成的串
3)子串:由串中任意长度的连续字符构成的序列,类似子集。
子串在主串中的位置是该子串(首席出现)的第一个字符在主串中的位置。
空串是任意串的子串,例:cb
4)主串:包含字符的串,例:abcddcc
5)串相等:两个串长度相等,且对应位置上的字符相同
6)串比较:依次比较字符ASCII码,先大者大,始终相等,串长者大
a:97 、A:95、0 :48
3 串的存储结构
串结束以 \0 结束
1)顺序存储
用一组地址连续的存储单元来存储串值的字符序列
2)链式存储
每个结点可存一/多个字符,考虑存储密度问题
KMP算法
1 概念:字符串匹配算法
2 实现:实现一个next()函数,函数本身包含了模式串的局部匹配信息
部分匹配表位数:
字符串(已匹配字符串)
1)前缀:除了最后一个字符外,所有以最后一个字符结尾的子串
2)后缀:除了第一一个字符外,所有以第一个字符开头的子串
3)部分匹配位数:前缀和后缀共有元素对应的长度
3 移动位数:已匹配位数-部分匹配位数
4 例题




图
1 概念:由两个集合V和E构成的二元组,记作:G=(V,E)。
V是顶点的非空有限集合
E是图中边的有限集合
2 1)有向图:G的每条边有方向;顶点间关系<vi,vj>
2)无向图:G的每条边都无方向;顶点关系(vi,vj)
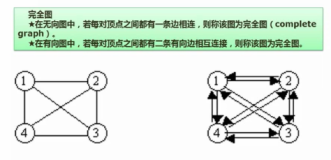
3)完全图:G的任意两个顶点都有一条边相连接
1)有向完全图:边数:n(n-1)
2)无向完全图:边数:n(n-1)/2
3 度:顶点V的度是与它相关联的边的条数,以下两者之和
1)入度:以V为终点的有向边的条数 ID(V)
2)出度:以V为始点的条数OD(V)
4 带权图
边上带权的图,权指每条边上的数
5 连通图
连通图:无向图中从一个结点到任意一个结点有路径相连。边的数目>=顶点数目-1
强连通图:对于任意两个顶点,存在到双方的有向路径。
6 生成树
1)极小连通子图,n个结点,n-1条边
若添加一条边,构成一个环,减去一条边,非联通图
2)最小生成树:带全路径和最小
7 图的存储结构
1)邻接矩阵
n个结点的图,可使用n*n的矩阵(二维数组)表示邻接关系
2)邻接表
由表头结点和表结点两部分组成
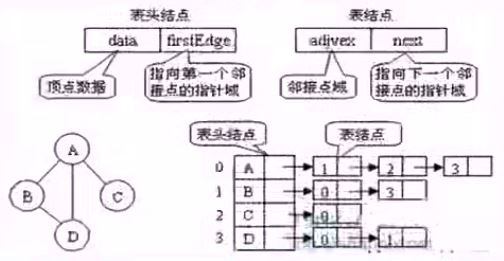
8 图的遍历
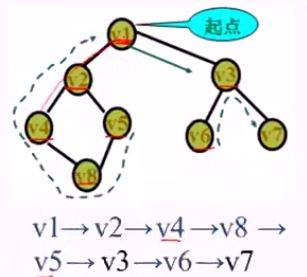
1)深度优先搜索(DFS)
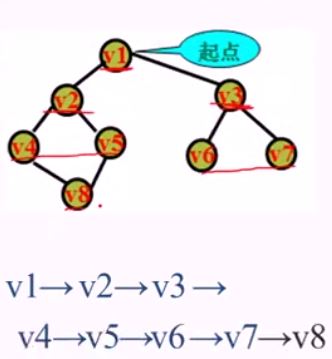
2)广度优先搜索(BFS)
拓扑排序
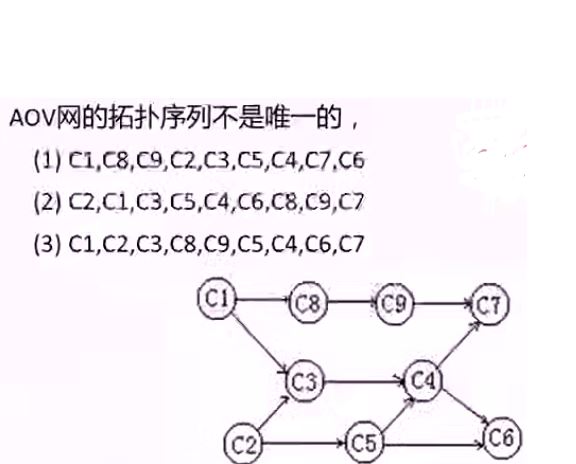
AOV网:有向无序图。类似前驱图
AOV顶点的顺序称为拓扑序列
拓扑排序:
1)从AOV网中选择一个没有前驱的顶点输出它
2)删除该顶点,且删除所有以该顶点为尾的弧
3)迭代
拓扑序列不唯一