用L2正则的线性回归模型,称为Ridge回归 (岭回归)
用L1正则的线性回归模型,称为LASSO回归

=== L2和L1的比较 ===
$color{red}{L2-norm正则}$,由于对于各个维度的参数缩放是在一个圆内缩放的,__(对各个维度的参数进行一个播报,在一个圆内进行播报)__,所以不可能导致有维度参数变成0的情况,那么也就不会产生$color{red}{稀疏解}$;实际应用中,数据的维度中是存在$color{red}{噪音}$和$color{red}{冗余}$的,稀疏的解可以找到有用的维度并减少冗余,提高预测的$color{red}{准确率}$和$color{red}{鲁棒性}$(减少了overfitting)。
L1-norm可以达到最终解的稀疏性要求。
Ridge模型具有较高的准确性、鲁棒性以及稳定性;
LASSO模型具有较高的求解速度;
如果即要考虑稳定性也考虑求解的速度,就使用Elastic Net。
什么是稀疏解?
对于一组参数θk,其中有一个或多个θ等于0,或近似等于0。称这组参数θk存在稀疏解。
如何理解:稀疏解可以找到有用的维度并减少冗余?
y=ax1+bx2+c;
若求解得到 a=3; b=0; c=2;
我们发现x2特征对于结果的预测没有任何帮助,所以可以将x2的特征删除。
注意:
L2-Ridge不产生稀疏解,L1-LASSO可以让解去冗余。
当我们觉得每个特征都是有用的,用L2。
如果想用回归的手段确定特征的可用性,用L1。
L1-LASSO有相对比较快的求解速度。
=== L1、L2的图像比较 ===
首先把特征降低至2维:
y=θ0+θ1x1+θ2x2
什么是把数据播放到圆内?
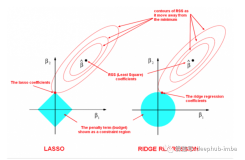
L1(左图)、L2(右图)中两团红色的圈圈是三维图像在二维平面上的映射。L1和L2两张图是中间图像的俯视图,要立体得去看:
先忽略正则项,只看损失函数对应的图像:
对于: y=θ0+θ1x1+θ2x2; θ1、θ2有一组对应的取值(Β1,Β2)
当θ向量取值为损失函数最小值的点,这个点就是Β^
Β^ 这一点是线性回归取得损失函数最优点的那个解。Β^:(Β1,Β2)
每一个小椭圆上,损失函数的值是相等的。
以Β^为圆心,越往外的椭圆损失值越大。
现在损失加入正则的情况:
加入正则惩罚项后,意味着现在的取值加入了新的约束条件,使得θ值必须在我的限制条件内才能被认可。
图像中,L1蓝色方块和L2蓝色椭圆的区域就是正则惩罚项中允许的θ值。什么时候能够取得最优的θ值?
$color{red}{显然当蓝色区域和红色椭圆“相切”的那一点就是最优的θ值。}$
回过头再次思考稀疏解的问题:
何为稀疏解?系数为0的时候。
在图中,即意味着Β1 = 0 或Β2 = 0 或Β1 = Β2 = 0;
在L1-norm和L2-norm中 (蓝色区域) ,显然Β1 = Β2 = 0 这点为圆心,相切的点不可能在圆心上,因此这点排除。
对于我们的L1和L2来说,损失函数中惩罚项的位置是固定的。
观察L2图像,为什么不能生成稀疏解:
而损失函数前半段的图像形状(红色椭圆),会根据y值(真实值)的改变而发生改变。如图:

损失函数和惩罚相相切的位置可能存在于任何一点。既然在惩罚项的圆上每一点都有可能相切,那么切到Β1 = 0或Β2 = 0的概率趋向于0。
所以,当选择L2-norm后,基本不可能出现稀疏解。
观察L1图像,为什么能够生成稀疏解:
如果损失函数和惩罚项相切了,意味红色椭圆和蓝色四边形的其他任意一点都不相交,意味着蓝色四边形边上的其他任意一点到B^ 的距离都不如相切的这一点到B^ 的距离近。

该图形中,各个点相切的概率不是相等的。切到顶点的概率是最高的。所以更容易产生稀疏解。
=== Elastic Net ===
如果即要考虑稳定性也考虑求解的速度,就使用Elastic Net。
同时使用L1正则和L2正则的线性回归模型就称为Elastic Net,$color{red}{弹性网络算法}$

p、λ都是超参数。
超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,给学习机选择一组最优超参数,以提高学习的性能和效果。
=== 案例 ===
根据四种不同的回归模型,在不同阶数下的回过结果如何。
## 创建模拟数据
## 使得随机数据可预测,即只要seed的值一样,后续生成的随机数都一样。
np.random.seed(100)
np.set_printoptions(linewidth=1000, suppress=True)#显示方式设置,每行的字符数用于插入换行符,是否使用科学计数法
N = 10
## linspace:x从0~6之间等步长取N个数
## 由于seed(10),固定了一种随机方案,np.random.randn(N)每次结果都一致
x = np.linspace(0, 6, N) + np.random.randn(N)
y = 1.8*x**3 + x**2 - 14*x - 7 + np.random.randn(N)
x.shape## 将其设置为矩阵
#无论多少数据,生成一列,反之1,-1生成一行
x.shape = -1, 1
y.shape = -1, 1
x.shape
y.shape将多个管道嵌套,共4个管道Pipeline
看看每个管道做了什么操作
管道1:多形式扩展+线性回归
管道2:多形式扩展+RidgeCV
管道3:多形式扩展+LassoCV
管道4:多形式扩展+ElasticNetCV
## RidgeCV和Ridge的区别是:前者可以进行交叉验证
## 目标:比较不同阶数的情况下,会不会出现过拟合的情况
models = [
Pipeline([
('Poly', PolynomialFeatures(include_bias=False)),
('Linear', LinearRegression(fit_intercept=False))
]),
Pipeline([
('Poly', PolynomialFeatures(include_bias=False)),
('Linear', RidgeCV(alphas=np.logspace(-3,2,50), fit_intercept=False))
]),
Pipeline([
('Poly', PolynomialFeatures(include_bias=False)),
('Linear', LassoCV(alphas=np.logspace(0,1,10), fit_intercept=False))
]),
Pipeline([
('Poly', PolynomialFeatures(include_bias=False)),
('Linear', ElasticNetCV(alphas=np.logspace(0,1,10),
l1_ratio=[.1, .5, .7, .9, .95, 1], fit_intercept=False))
])
]## 线性回归、Lasso回归、Ridge回归、ElasticNet比较
plt.figure(facecolor='w')
degree = np.arange(1,N, 2) # 阶
dm = degree.size
colors = [] # 颜色
for c in np.linspace(16711680, 255, dm):
colors.append('#%06x' % int(c))
titles = [u'线性回归', u'Ridge回归', u'Lasso回归', u'ElasticNet']
for t in range(4):
model = models[t]#选择了模型--具体的pipeline
plt.subplot(2,2,t+1)
plt.plot(x, y, 'ro', ms=10, zorder=N)
for i,d in enumerate(degree):
# 设置阶数(多项式)
model.set_params(Poly__degree=d)
# 模型训练
model.fit(x, y.ravel())
# 获取得到具体的算法模型
lin = model.get_params('Linear')['Linear']
# 打印数据
output = u'%s:%d阶,系数为:' % (titles[t],d)
print (output, lin.coef_.ravel())
# 产生模拟数据
x_hat = np.linspace(x.min(), x.max(), num=100) ## 产生模拟数据
x_hat.shape = -1,1
# 数据预测
y_hat = model.predict(x_hat)
# 计算准确率
s = model.score(x, y)
#
z = N - 1 if (d == 2) else 0
label = u'%d阶, 正确率=%.3f' % (d,s)
plt.plot(x_hat, y_hat, color=colors[i], lw=2, alpha=0.75, label=label, zorder=z)
plt.legend(loc = 'upper left')
plt.grid(True)
plt.title(titles[t])
plt.xlabel('X', fontsize=16)
plt.ylabel('Y', fontsize=16)
plt.tight_layout(1, rect=(0,0,1,0.95))
plt.suptitle(u'各种不同线性回归过拟合显示', fontsize=22)
plt.show()线性回归:1阶,系数为: [-44.14102611 40.05964256]
线性回归:3阶,系数为: [ -6.80525963 -13.743068 0.93453895 1.79844791]
线性回归:5阶,系数为: [ -5.60899679 -14.80109301 0.75014858 2.11170671 -0.07724668 0.00566633]
线性回归:7阶,系数为: [-41.70721172 52.38570529 -29.56451338 -7.66322829 12.07162703 -3.86969096 0.53286096 -0.02725536]
线性回归:9阶,系数为: [-2465.58381316 6108.63817712 -5111.99333504 974.74974891 1078.89649478 -829.50277842 266.13230658 -45.71741587 4.1158274 -0.15281063]
Ridge回归:1阶,系数为: [ 29.87629065]
Ridge回归:3阶,系数为: [-12.98191422 -0.50844765 1.98772916]
Ridge回归:5阶,系数为: [-18.76655299 -0.28947771 3.32509764 -0.35027494 0.02456036]
Ridge回归:7阶,系数为: [-17.34640888 -3.48657706 4.33150776 0.39729204 -0.45104331 0.08994449 -0.0056256 ]
Ridge回归:9阶,系数为: [-2.2521578 -2.27937783 -1.70299005 -1.0348803 0.85755012 0.37020601 -0.26024292 0.04709033 -0.00277978]
Lasso回归:1阶,系数为: [ 30.30898284]
Lasso回归:3阶,系数为: [-12.31558512 -0.50643475 1.96415216]
Lasso回归:5阶,系数为: [-12.49095935 -0.5462019 1.85689229 0.04796991 -0.00459415]
Lasso回归:7阶,系数为: [-0. -0.42783947 -0.52239776 0.41588259 0.0107619 -0.00095271 -0.00041016]
Lasso回归:9阶,系数为: [-12.78111829 -0.49882979 1.80841074 0.03631125 0.00358085 -0.0003109 -0.00003417 -0.00000479 -0.00000044]
ElasticNet:1阶,系数为: [ 28.51169563]
ElasticNet:3阶,系数为: [-10.72359515 -1.20646101 2.03645101]
ElasticNet:5阶,系数为: [-5.90338414 -1.62213355 1.13077809 0.2390498 -0.01640652]
ElasticNet:7阶,系数为: [-0. -0.501937 -0.51930136 0.42305198 0.00992334 -0.00096761 -0.00041003]
ElasticNet:9阶,系数为: [-0.59980891 -0.53028001 -0.49033227 0.40675528 0.00848508 0.00000901 -0.00016187 -0.00002562 -0.00000379]

数据来源: 07 过拟合欠拟合 - 案例