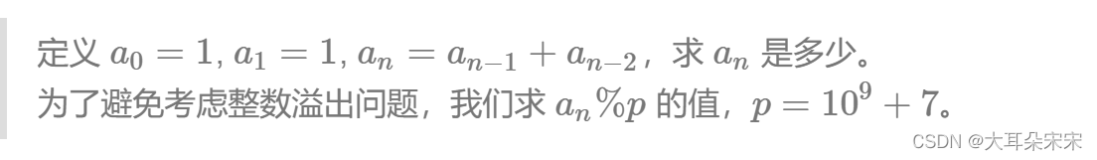网址:http://acm.nefu.edu.cn/test/problemshow.php
题意:f[1] = 1; f[2] = 2;f[n] = f[n - 1] + f[n - 2];
And s[n] is defined:
 ans = as[x] % n;
ans = as[x] % n;
根据性质:f[0]^2+f[1]^2+...+f[n]^2=f[n]*f[n+1]
ans=a^(f[x]*f[x+1]-1)%n再根据欧拉定理向下降幂就可以了。
#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAX=2;
typedef long long int64;
typedef long long ll;
long long M;
bool f;
typedef struct
{
long long m[MAX][MAX];
} Matrix;
Matrix P=
{
1,1,
1,0,
};
Matrix I=
{
1,0,
0,1,
};
Matrix matrixmul(Matrix a,Matrix b) //矩阵乘法
{
int i,j,k;
Matrix c;
for (i = 0 ; i < MAX; i++)
for (j = 0; j < MAX; j++)
{
c.m[i][j] = 0;
for (k=0; k<MAX; k++)
{
c.m[i][j]+=(a.m[i][k]*b.m[k][j]);
if(c.m[i][j]>M)
c.m[i][j]%=M,f=1;
}
c.m[i][j]%=M;
}
return c;
}
Matrix quickpow(long long n)
{
Matrix m = P, b = I;
while (n >= 1)
{
if (n & 1)
b = matrixmul(b,m);
n = n >> 1;
m = matrixmul(m,m);
}
return b;
}
long long phi(long long n)
{
long long rea=n;
for(long long i=2; i*i<=n; i++)
if(n%i==0)
{
rea=rea-rea/i;
do
n/=i;
while(n%i==0);
}
if(n>1)
rea=rea-rea/n;
return rea;
}
long long Mulmod(ll a,ll b,ll n)
{
ll exp = a%n, res = 0;
while(b)
{
if(b&1)
{
res += exp;
if(res>n) res -= n;
}
exp <<= 1;
if(exp>n)
exp -= n;
b>>=1;
}
return res;
}
long long exp_mod(ll a,ll b,ll c)
{
ll k = 1;
while(b)
{
if(b&1)
k = k*a%c;
a = a*a%c;
b>>=1;
}
return k;
}
int main()
{
long long a,x,n,s;
while(~scanf("%lld%lld%lld",&a,&x,&n),a+x+n)
{
f=0;
M=phi(n);
if(x==1)
s=1;
else if(x==2)
s=5;
else
{
Matrix ans=quickpow(x-2);
long long s1=ans.m[0][0]*2+ans.m[0][1];
ans=matrixmul(ans,P);
long long s2=ans.m[0][0]*2+ans.m[0][1];
if(f||s1*s2>M)
f=1,s=Mulmod(s1,s2,M)-1,s=s<0?s+M:s;
else
s=s1*s2-1;
}
if(s>M)
s%=M,f=1;
long long ansn;
if(f)
ansn=exp_mod(a,s+M,n);
else
ansn=exp_mod(a,s,n);
printf("%lld\n",ansn);
}
return 0;
}