卷积
卷积就是滑动中提取特征的过程
在数学中,卷积convolution是一种函数的定义。它是通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与g经过翻转和平移的重叠部分的面积。其定义为:
$h(x)=f(x)*g(x) =\int_{-\infty}^{\infty}f(t)g(x-t)dt$
也可以用星号表示:$h(x)=(f*g)(x)$
卷积的第一个参数(上例中的f),通常叫做输入。第二个参数(函数g)叫做核函数kernel function。输出有时候叫特征映射feature map.
也可以定义离散形式的卷积:
$h(x)=(f*g)(x) = \sum_{t=-\infty}^{\infty}f(t)g(x-t)$
g(x-t)是变化的,而f(t)是固定不动的。我们可以将卷积理解成是g(x-t)滑动过程中对f(t)进行采样。
我们一般可以用$f(x)=wx+b$来作为核函数提取特征
我们来举个小例子说明一下卷积对于特征提取的过程。
假设有一个5*5的矩阵做为输入:
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]], dtype=float32)y=wx+b我们取w为3*3的全1矩阵,b=0。
这样我们计算左边第一个3*3的小块,得$1*1+1*1+1*1+1*1+1*1+1*1+1*1+1*1+1*1=9$。
以此类推,最后我们得到一个
[[9,9,9],
[9,9,9],
[9,9,9]]
的矩阵。
相当于我们把一个55的黑白矩阵压缩成了33的灰度矩阵。
全是1的话大家看不太清楚,我们选一个对角矩阵再来计算一下:
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]], dtype=float32)计算卷积之后的结果为:
[[3,2,1],
[2,3,2],
[1,2,3]]图像缩小了之后,仍然是主对角线最黑。基本特征还是被提取出来了。
填充Padding
从前面对角线的例子可以看出,由于图片中间的点被计算的次数多,而边缘上的点计算的次数少,所以明明右上角和左下角都是0,提取完特征之后被中间的1给影响了。
我们可以选择给这个55的矩阵外边加上一圈padding,将其变成77的矩阵。
我们再重新计算一下卷积,获取下面一个5*5的新矩阵:
[[2,2,1,0,0],
[2,3,2,1,0],
[1,2,3,2,1],
[0,1,2,3,2],
[0,0,1,2,2]]这样边缘的0就被识别出来了。Padding的最主要作用就是让边界变得更清晰。
步幅Stride
上面我们求卷积的时候,每次向右移到一步,这个移动距离就是Stride。
比如我们想把图片压缩得更狠一点,取得更高的压缩率,我们就可以加大步幅。
卷积用Tensorflow实现
上面知识储备已足,我们开始用Tensorflow来计算卷积吧。
首先是输入,按照Tensorflow的要求,我们得把5*5的,resize成[1,5,5,1]格式的,如下:
>>> c
array([[[[1.],
[0.],
[0.],
[0.],
[0.]],
[[0.],
[1.],
[0.],
[0.],
[0.]],
[[0.],
[0.],
[1.],
[0.],
[0.]],
[[0.],
[0.],
[0.],
[1.],
[0.]],
[[0.],
[0.],
[0.],
[0.],
[1.]]]], dtype=float32)然后我们还需要准备卷积核,先生成一个3*3全1矩阵:
>>> a2 = sess.run(tf.ones([3,3]))
>>> a2
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]], dtype=float32)然后将其reshape成[3,3,1,1]格式的:
>>> a3 = sess.run(tf.reshape(a2,[3,3,1,1]))
>>> a3
array([[[[1.]],
[[1.]],
[[1.]]],
[[[1.]],
[[1.]],
[[1.]]],
[[[1.]],
[[1.]],
[[1.]]]], dtype=float32)步幅我们设成[1,1,1,1],其实就是x轴1,y轴1,前面和后面的1先不用管它。padding设成'SAME':
>>> a1 = tf.nn.conv2d(c,a3,strides=[1,1,1,1],padding='SAME')
>>> sess.run(a1)
array([[[[2.],
[2.],
[1.],
[0.],
[0.]],
[[2.],
[3.],
[2.],
[1.],
[0.]],
[[1.],
[2.],
[3.],
[2.],
[1.]],
[[0.],
[1.],
[2.],
[3.],
[2.]],
[[0.],
[0.],
[1.],
[2.],
[2.]]]], dtype=float32)结果看起来不爽的话,我们再重新将其reshape成[5,5]的:
>>> a5 = tf.reshape(a4,[5,5])
>>> sess.run(a5)
array([[2., 2., 1., 0., 0.],
[2., 3., 2., 1., 0.],
[1., 2., 3., 2., 1.],
[0., 1., 2., 3., 2.],
[0., 0., 1., 2., 2.]], dtype=float32)嗯,是不是跟我们手动计算的一样呢?恭喜你,已经学会卷积啦!
池化层
池化层跟卷积也很像,但是计算要简单得多。池化主要有两种,一种是取最大值,一种是取平均值。而卷积是要做矩阵内积运算的。
我们以2*2最大池化为例,处理一下上节加了padding的卷积
[[2,2,1,0,0],
[2,3,2,1,0],
[1,2,3,2,1],
[0,1,2,3,2],
[0,0,1,2,2]]最大池化就是取最大值,比如[[2,2],[2,3]]就取3。结果如下:
[[3,3,2,1],
[3,3,3,2],
[2,3,3,3],
[1,2,3,3,]]可以看到,池化虽然进一步丢失了信息,但是基本规律还是不变的。
池化被认为可以提高泛化性,对于微小的变动不敏感。比如对于少量的平移,旋转或者缩放保持同样的识别。但是,池化层不是必须的。
在Tensorflow中,可以用tf.nn.max_pool来实现最大池功能。
首先我们要把图片resize成(-1,高,宽,1)这样格式的:
>>> b = tf.reshape(a,[-1,5,5,1])
>>> c = sess.run(b)
array([[[[1.],
[0.],
[0.],
[0.],
[0.]],
[[0.],
[1.],
[0.],
[0.],
[0.]],
[[0.],
[0.],
[1.],
[0.],
[0.]],
[[0.],
[0.],
[0.],
[1.],
[0.]],
[[0.],
[0.],
[0.],
[0.],
[1.]]]], dtype=float32)然后我们用步幅为2。2*2窗口计算max pooling。
命令如下:
d =tf.nn.max_pool(c,ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')四元组中我们不必管第一个和最后一个,中间两个是高和宽。ksize和步幅皆如此。
运行结果是一个3*3的对角阵:
>>> sess.run(d)
array([[[[1.],
[0.],
[0.]],
[[0.],
[1.],
[0.]],
[[0.],
[0.],
[1.]]]], dtype=float32)卷积网络的结构
卷积神经网络也叫卷积网络,是一种善于处理网格数据的网络。典型应用是处理一维网格数据语音和二维网格数据图像。只要是在网络结构中使用了哪怕一层的卷积层,就叫做卷积神经网络。
与之前介绍的神经网络都是全连接网络,即每一层的每个节点都是上一层的所有节点相连接。
而卷积网络一般是五种连接结构的组合:
- 输入层:一般认为就是原图片
- 卷积层:与全连接网络不同,卷积层中每一个节点的输入只是上一层神经网络的一小块,常用的块大小为33或者55。一般来说,通过卷积层处理过的节点的矩阵的深度会变深
- 池化层:Pooling层不会改变矩阵的深度,但是会使矩阵变小。可以理解为池化层是把高分辨率的图片转化成低分辨率的图片
- 全连接层:最后的分类工作一般还是由一至两个全连接层来实现的。
- Softmask层:可以得到当前样例属于不同分类的概率情况
卷积网络简史
上节深度学习简史中我们提到过,第一个卷积网络模型于1989年由Yann LeCun提出。卷积网络的主要概念如为什么要卷积,为什么要降采样,什么是径向基函数RBF(Radial Basis Function)等。
10年后的1998年,Yann LeCun设计了LeNet网络。在论文《Gradient-Based Learning Applied to Document Recognition》中提出了LeNet-5的模型,结构如下: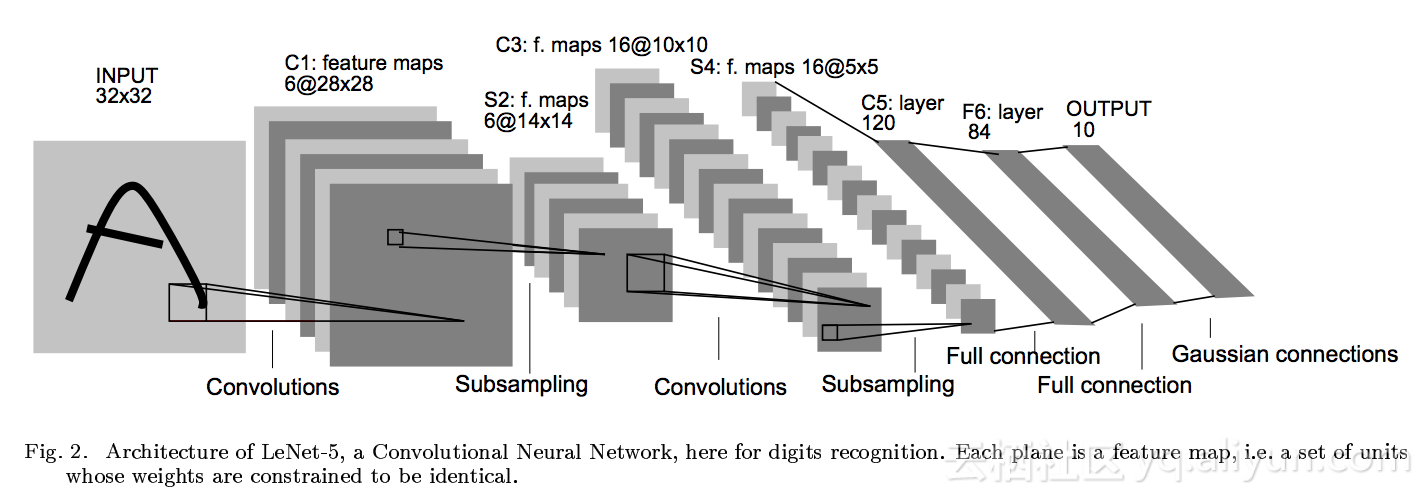
论文原文在:http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf
但是,正如我们前面介绍的,当时还是SVM辉煌的时代。
转折点要到十几年后的2012年,Hinton的学生Alex Krizhevsky发明的AlexNet之时。AlexNet在2012年的图像分类竞赛中将Top-5错误率从上一年的25.8%降到15.3%.
AlexNet成功之后,大家的研究热情空前高涨。主要方向有网络加深和功能增强。
- 网络加深:深度学习的优势就是突破了加深层数的关键点。那么就可以构建比AlexNet层数更多的网络。代表作是2014年ImageNet比赛的亚军牛津大学的VGGNet,它的层数可以达到16~19层。从而将Top-5错误率从AlexNet的15.3%降到了7.32%.
- 功能增强:代表作是GoogLeNet。GoogLeNet参考了NIN(Network In Network)的思想,将原来的线性卷积层改成了多层感知机。同时,将全连接层改进为全局平均池化。功能增强之后,GoogLeNet力压VGGNet,获得2014年ImageNet的冠军,将Top-5错误率降到6.67%. 虽然功能有增强,但是在层数上GoogLeNet也毫没客气地增加到22层。后来在GoogLeNet的基础上又推出Inception V3, V4等网络。
- 既加深也增强:代表作是2015年的ImageNet分类冠军,由微软亚洲研究院发明的ResNet残差网络。ResNet在2015年的成绩把错误率降到3.57%.
话说ImageNet真是个群英荟萃的地方。2012年第一名是Alex。2013的第一名是Matthew Zeiler,之前讲过他提出的AdaGrad。
值得一提的是,在最近几年的ImageNet中,华人屡创佳绩。比如2016年的冠军被公安部第三研究所搜神团队获得,成绩是错误率2.99%。