随机森林特征选择法 —— Gini Importance
原理:
使用Gini指数表示节点的纯度,Gini指数越大纯度越低。然后计算每个节点的Gini 指数 - 子节点的Gini 指数之和,记为Gini decrease。最后将所有树上相同特征节点的Gini decrease加权的和记为Gini importance,该数值会在0-1之间,该数值越大即代表该节点(特征)重要性越大。
涉及参数计算:
Gini index:衡量决策树每一棵树上的节点上面所存在的数据的纯净度的一个指标。这个值越小,纯净度越高。
公式: 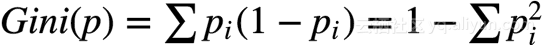
$p_{i}$是节点内各个特征所占的概率。
OK,原理不再多说了。
更多请看我之前写的博客:
Gini decrease:每个节点的Gini index - 子节点的Gini index之和(这里的和是加权和)。
Gini importance:将所有树上相同特征节点的Gini decrease加权的和。
需要注意的问题:
1、这种方法存在偏向,对具有更多取值的特征会更有利;
2、对于存在关联的多个特征,其中任意一个都可以作为指示器(优秀的特征),并且一旦某个特征被选择之后,其他特征的重要度就会急剧下降,因为不纯度已经被选中的那个特征降下来了,其他的特征就很难再降低那么多不纯度了,这样一来,只有先被选中的那个特征重要度很高,其他的关联特征重要度往往较低。在理解数据时,这就会造成误解,导致错误的认为先被选中的特征是很重要的,而其余的特征是不重要的,但实际上这些特征对响应变量的作用确实非常接近的(这跟Lasso是很像的)。
Python实现:
import pandas
import numpy as np
from sklearn import ensemble
from sklearn.preprocessing import LabelEncoder
iris =pandas.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',header=None)
iris.columns=['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']
le = LabelEncoder()
le.fit(iris['Species'])
rf = ensemble.RandomForestClassifier()
features = ['PetalLengthCm','PetalWidthCm','SepalLengthCm','SepalWidthCm']
y = np.array(le.transform(iris['Species']))
X = np.array(iris[features])
#Gini importance
rf.fit(X,y)
print(rf.feature_importances_)[ 0.34870355 0.52788187 0.10220203 0.02121255]
随机森林特征选择法 —— Mean Decrease Accuracy
原理:主要思路是打乱每个特征的特征值顺序,并且度量顺序变动对模型的精确率的影响。很明显,对于不重要的变量来说,打乱顺序对模型的精确率影响不会太大,但是对于重要的变量来说,打乱顺序就会降低模型的精确率。
实现步骤:
1.训练出一个随机森林模型,在测试集检验得到accuracy0;
2.随机重排(permutation)测试集某特征xi,检验得到accuracyi;
3.(accuracy0 - accuracyi)/accuracy0,即为特征xi的重要性。
Python实现:
from sklearn.metrics import accuracy_score
from sklearn.model_selection import ShuffleSplit
rs = ShuffleSplit(n_splits=10,test_size=0.1)
scores = np.zeros((10,4))
count = 0
for train_idx, test_idx in rs.split(X):
X_train , X_test = X[train_idx] , X[test_idx]
y_train , y_test = y[train_idx] , y[test_idx]
r = rf.fit(X_train,y_train)
acc = accuracy_score(y_test,rf.predict(X_test))
for i in range(len(features)):
X_t = X_test.copy()
np.random.shuffle(X_t[:, i])
shuff_acc = accuracy_score(y_test,rf.predict(X_t))
scores[count,i] = ((acc-shuff_acc)/acc)
count += 1
print(np.mean(scores,axis=0))[ 0.24150183 0.35630037 0.00666667 0. ]
可以看出来,前两个特征是比后两个特征重要得多的。
线性回归特征选择:L1正则化Lasso
什么是正则化?:监督机器学习问题无非就是“minimize your error while regularizing your parameters”,也就是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。
正则化的作用:
1、约束参数,降低模型复杂度。
2、规则项的使用还可以约束我们的模型的特性。这样就可以将人对这个模型的先验知识融入到模型的学习当中,强行地让学习到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。
L1范数:向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。
L1范数的作用:由于L1范数的天然性质,对L1优化的解是一个稀疏解,因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
L1正则化Lasso
- 普通线性回归:
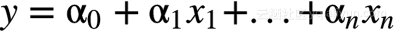
- 普通线性回归目标函数:
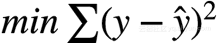
- Lasso目标函数:
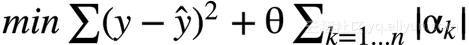
其中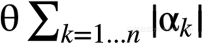
是L1正则化项。θ越大,对于系数α的惩罚就会越严重,所以会有更多的系数倾向于0(因为要使目标函数尽可能小,所以系数α会尽量变小);θ越小,对于系数α的惩罚就越轻,回归得到的系数会越接近于普通线性回归。
L1正则化python实现:
import pandas
import numpy as np
from sklearn import linear_model
from sklearn.preprocessing import LabelEncoder
iris = pandas.read_csv("iris.csv")
le = LabelEncoder()
le.fit(iris['Species'])
lm = linear_model.Lasso(0.02)
features = ['PetalLengthCm','PetalWidthCm','SepalLengthCm','SepalWidthCm']
y = np.array(le.transform(iris['Species']))
X = np.array(iris[features])
lm.fit(X,y)
print(lm.coef_)[ 0.28777819 0.35160589 -0. -0. ]
同样的,通过L1正则化Lasso,我们也得到了前两个特征比后两个重要。








