一,介绍
本文介绍使用Kruskal算法求解无向图的最小生成树。Kruskal是一个贪心算法,并且使用了并查集这种数据结构。
关于并查集的介绍,参考:数据结构--并查集的原理及实现
二,构造一个无向图
图,肯定有顶点和边。由于求解最小生成树,故边还需要有权值。此外,对于每一条边,需要找到与它相关联的两个顶点,因为在将这条边加入到最小生成树时需要判断这两个顶点是否已经连通了。顶点类定义如下:
1 private class Vertex { 2 private String vertexLabel; 3 private List<Edge> adjEdges;// 邻接表 4 5 public Vertex(String vertexLabel) { 6 this.vertexLabel = vertexLabel; 7 adjEdges = new LinkedList<Edge>(); 8 } 9 }
表明,图是采用邻接表的形式存储的。
边类的定义如下:
1 private class Edge implements Comparable<Edge> { 2 private Vertex startVertex; 3 private Vertex endVertex; 4 private int weight;// 边的权值 5 6 public Edge(Vertex start, Vertex end, int weight) { 7 this.startVertex = start; 8 this.endVertex = end; 9 this.weight = weight; 10 } 11 12 @Override 13 public int compareTo(Edge e) { 14 15 if (weight > e.weight) 16 return 1; 17 else if (weight < e.weight) 18 return -1; 19 else 20 return 0; 21 } 22 }
边实现了Comparable接口。因为,Kruskal算法使用优先级队列来存储边,边根据权值来进行比较。
假设图存储在一个文件中,每一行包含如下的信息:LinkID,SourceID,DestinationID,Cost(边的编号,起始顶点的标识,终点的标识,边上的权值)
文件格式如下:
无向图如下:
private Map<String, Vertex> nonDirectedGraph;
另外,用一个Map来存储图的顶点,图采用邻接表形式表示。Map的Key为顶点的标识,Value为顶点类。
三,求解最小生成树的Kruskal算法分析
Kruskal算法是一个贪心算法,它与Dijkstra算法非常的相似。Kruskal算法贪心的地方在于:它总是选取图中当前权值最小的边的加入到树中(该边加入到树中之后不能出现环)。因此,这里就有个问题,如何选取当前权值最小的边?
Kruskal算法用到了并查集。因为,算法初始时将图中的各个顶点视为独立的,不连通的,随着一步步将当前权值最小的边加入,就将各个顶点连接起来了(使用并查集的Union操作实现连接)
关于选取最小权值的边,最常用的就是使用优先级队列了,而优先级队列则可以使用二叉堆来实现。关于二叉堆参考:数据结构--堆的实现(下)
算法的总体步骤:
①构造一个无向图啊。求解该图的最小生成树。----需要测试代码是否正确,得有一个实际的图。
②根据无向图中的顶点来 初始化 并查集----初始化过程和 并查集的应用之求解无向图中的连接分量个数 里面讲到的图的初始化过程一样。
③创建一个优先级队列来存储图中的边,这样每次选取边时,直接出队列,这比查找图中所有的边然后选择最小权值的边效率要高一点啊。
④判断这条边关联的两个顶点是否已经连通,如果已经连通了,再将该边加入到生成树中会导致环。
⑤直到所有的顶点都已经并入到生成树时,算法结束。
看完这个过程,感觉这个算法和并查集的应用之求解无向图中的连接分量个数--求解连通分量的算法没啥大区别。
只不过Kruskal算法额外多用了一个优先级队列而已。
四,代码实现
Kruskal算法用到并查集,那肯定需要实现并查集的基本操作,关于并查集,参考:数据结构--并查集的原理及实现
关于并查集基本操作的实现与并查集的应用之求解无向图中的连接分量个数 基本一样。
关于存储并查集的一维数组的说明如下:
使用一个一维数组来存储并查集,这里一维数组的下标表示图的顶点标识,数组元素s[i]有两种表示含义:当数组元素大于0时,表示的是 顶点 i 的父结点位置 ;当数组元素s[i]小于0时,表示的是 顶点 i 为根的子树的高度(秩!)。从而将数组的下标与图的顶点一 一 对应起来。
下面重点来看下最小生成树算法的实现:
1 /** 2 * 3 * @param graph 4 * 求解graph的一棵最小生成树 5 * @return 组成最小生成树上的所有的边 6 */ 7 public List<Edge> kruskal(Map<String, Vertex> graph) { 8 List<Edge> miniEdges = new ArrayList<Edge>(graph.size() - 1); 9 10 while (miniEdges.size() != graph.size() - 1) { 11 Edge e = pq.remove(); 12 int start = Integer.valueOf(e.startVertex.vertexLabel); 13 int end = Integer.valueOf(e.endVertex.vertexLabel); 14 if (find(start) != find(end)) { 15 union(start, end); 16 miniEdges.add(e); 17 } 18 } 19 return miniEdges; 20 }
第8行构造一个ArrayList存储最小生成树中的边。其中,最小生成树中的边的数目为顶点的数目减1。graph.size()返回顶点的个数。
在第10行的while循环中构建最小生成树,第12行和第13行获得顶点的标识。顶点的标识与数组下标对应,比如 顶点4 ’存储‘ 在 s数组中的下标4中。
第14行判断两个顶点是否已经连通,若不连通,则将这条边加入到最小生成树中。初始时,所有的顶点都在各自的子树中,互不连通(见make_set方法)
关于算法效率的一点分析:
上面的方法中,不断地从优先级队列中弹出权值最小的边,在大部分的情况下,是不需要将优先级队列中的所有的边都弹出完的。
但是,存在这样一种情况:图中权值最大的那条边是唯一到某个顶点的路径,则需要把优先级队列中的所有的边都弹出后,才能构造一棵最小生成树。
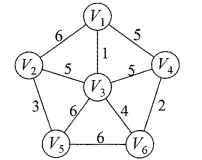
就拿上面的那个图来说:顶点4到 顶点6 这条边的权值为6,是所有边的最大的,而且到达顶点4只能经过 权值为6 的这条边。而我们所有的边都存储在优先级队列中,故权值为6这条边一定是最后才弹出的,在权值为6的这条边出队列时,图中所有的边都已经出队列了(优先级队列嘛,权值越小,越先出队列)。
假设把顶点4到 顶点6 这条边的权值 6改成 1,在 顶点2 到 顶点5的权值为5的边、顶点3到 顶点6 权值为4 的边 出队列之前,最小生成树就已经构造好了。
因为,优先级队列会优先选择顶点3到顶点2的这条边,以及 顶点5 到 顶点6的边。
五,整个完整代码如下:
1 import java.util.ArrayList; 2 import java.util.LinkedHashMap; 3 import java.util.LinkedList; 4 import java.util.List; 5 import java.util.Map; 6 import java.util.PriorityQueue; 7 8 import c9.topo.FileUtil; 9 10 public class MinSpanningTree { 11 private class Vertex { 12 private String vertexLabel; 13 private List<Edge> adjEdges;// 邻接表 14 15 public Vertex(String vertexLabel) { 16 this.vertexLabel = vertexLabel; 17 adjEdges = new LinkedList<Edge>(); 18 } 19 } 20 21 private class Edge implements Comparable<Edge> { 22 private Vertex startVertex; 23 private Vertex endVertex; 24 private int weight;// 边的权值 25 26 public Edge(Vertex start, Vertex end, int weight) { 27 this.startVertex = start; 28 this.endVertex = end; 29 this.weight = weight; 30 } 31 32 @Override 33 public int compareTo(Edge e) { 34 35 if (weight > e.weight) 36 return 1; 37 else if (weight < e.weight) 38 return -1; 39 else 40 return 0; 41 } 42 } 43 44 private Map<String, Vertex> nonDirectedGraph; 45 PriorityQueue<Edge> pq = new PriorityQueue<MinSpanningTree.Edge>();// 优先级队列存储边 46 47 private void buildGraph(String graphContent) { 48 String[] lines = graphContent.split("\n"); 49 50 String startNodeLabel, endNodeLabel; 51 Vertex startNode, endNode; 52 for (int i = 0; i < lines.length; i++) { 53 String[] nodesInfo = lines[i].split(","); 54 startNodeLabel = nodesInfo[1]; 55 endNodeLabel = nodesInfo[2]; 56 57 endNode = nonDirectedGraph.get(endNodeLabel); 58 if (endNode == null) { 59 endNode = new Vertex(endNodeLabel); 60 nonDirectedGraph.put(endNodeLabel, endNode); 61 } 62 63 startNode = nonDirectedGraph.get(startNodeLabel); 64 if (startNode == null) { 65 startNode = new Vertex(startNodeLabel); 66 nonDirectedGraph.put(startNodeLabel, startNode); 67 } 68 Edge e = new Edge(startNode, endNode, Integer.valueOf(nodesInfo[3])); 69 // 对于无向图而言,起点和终点都要添加边 70 endNode.adjEdges.add(e); 71 startNode.adjEdges.add(e); 72 73 pq.add(e);// 将边加入到优先级队列中 74 } 75 } 76 77 private int[] s;// 存储并查集的一维数组 78 79 public MinSpanningTree(String graphContent) { 80 nonDirectedGraph = new LinkedHashMap<String, MinSpanningTree.Vertex>(); 81 buildGraph(graphContent); 82 83 make_set(nonDirectedGraph);// 初始化并查集 84 } 85 86 private void make_set(Map<String, Vertex> graph) { 87 int size = graph.size(); 88 s = new int[size]; 89 for (Vertex v : graph.values()) { 90 s[Integer.valueOf(v.vertexLabel)] = -1;// 顶点的标识是从0开始连续的数字 91 } 92 } 93 94 private int find(int root) { 95 if (s[root] < 0) 96 return root; 97 else 98 return s[root] = find(s[root]); 99 } 100 101 private void union(int root1, int root2) { 102 if (find(root1) == find(root2)) 103 return; 104 // union中的参数是合并任意两个顶点,但是对于并查集,合并的对象是该顶点所在集合的代表顶点(根顶点) 105 root1 = find(root1);// 查找顶点root1所在的子树的根 106 root2 = find(root2);// 查找顶点root2所在的子树的根 107 108 if (s[root2] < s[root1])// root2 is deeper 109 s[root1] = root2; 110 else { 111 if (s[root1] == s[root2])// 一样高 112 s[root1]--;// 合并得到的新的子树高度增1 (以root1作为新的子树的根) 113 s[root2] = root1;// root1 is deeper 114 } 115 } 116 117 /** 118 * 119 * @param graph 120 * 求解graph的一棵最小生成树 121 * @return 组成最小生成树上的所有的边 122 */ 123 public List<Edge> kruskal(Map<String, Vertex> graph) { 124 List<Edge> miniEdges = new ArrayList<Edge>(graph.size() - 1); 125 126 while (miniEdges.size() != graph.size() - 1) { 127 Edge e = pq.remove(); 128 //生成并查集操作的对应的标点位置 129 int start = Integer.valueOf(e.startVertex.vertexLabel); 130 int end = Integer.valueOf(e.endVertex.vertexLabel); 131 if (find(start) != find(end)) { 132 union(start, end); 133 miniEdges.add(e); 134 } 135 } 136 return miniEdges; 137 } 138 139 // for test purpose 140 public static void main(String[] args) { 141 String graphFilePath; 142 if (args.length == 0) 143 graphFilePath = "F:\\graph.txt"; 144 else 145 graphFilePath = args[0]; 146 147 String graphContent = FileUtil.read(graphFilePath, null);// 从文件中读取图的数据 148 MinSpanningTree mst = new MinSpanningTree(graphContent); 149 150 // 获得图中组成最小生成树的所有边 151 List<Edge> edges = mst.kruskal(mst.nonDirectedGraph); 152 for (Edge edge : edges) { 153 System.out.print(edge.startVertex.vertexLabel + "-->" 154 + edge.endVertex.vertexLabel); 155 System.out.println(" weight: " + edge.weight); 156 } 157 } 158 }
FileUtil类可参考中的完整代码实现。
六,实验结果
求得的最小生成树的信息如下:
0-->3 表示顶点0到顶点3的边,边的权值为1
5-->6 表示顶点5到顶点6的边,边的权值为1
.......