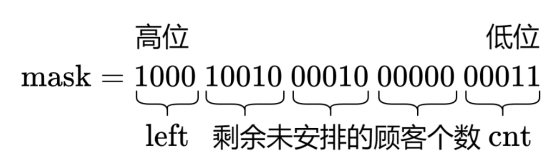
Description
ycc
喜欢古典音乐是一个 ZJUTACM
集训队中大家都知道的事情。为了更方便地聆听音乐,最近 ycc
特意把他的家搬到了爱乐大街(德语Philharmoniker-Straße
)。在爱乐大街上,依次坐落着N座跟音乐有关的建筑,比如音乐厅、歌剧院等建筑。走在爱乐大街的路上,ycc 感到非常满意。过了一会儿,ycc 开始对这些建筑的门牌号产生了兴趣,这 N 个建筑各自有
唯一的门牌号,范围从 1 到 N 。不过大概住在爱乐大街上的人都比较文艺,不喜欢循规蹈矩,他发现爱乐大街的门牌号并不是按照空间顺序依次从 1 到 N 的,而是任意顺序的,而且似乎没有什么规律可循。
ycc
不太习惯,于是他在纸上依次记录了每个建筑的门牌号,将他们写成一列。然后他在纸上开始比划起来。他发现门牌序列的逆序对个数为 K
。什么是逆序对呢?简单地说,就是两个门牌号,号码小的门牌号在号码大的门牌号后面。比如假设 N = 4
,且门牌号序列是 1 3 4 2
,那么这个序列的逆序对就有 (4, 2)
和 (3, 2)
两对,也就是说逆序对个数 K = 2
。那么现在,告诉你爱乐大街的建筑个数 N
和序列的逆序对个数 K
,你知道爱乐大街的门牌号序列是怎么样的吗?
Input
第一行一个整数 T
,表示有 T
组数据。
每组数据有两个整数 N (1
≤ N
≤ 10
5)
和 K (0
≤ K
≤ N(N - 1) / 2
且 K
≤ 10
8)
,分别表示爱乐大街上的建筑个数和门牌号序列的逆序对个数。
Output
在一行中输出空格隔开的 N
个数(行末没有空格),表示原来的门牌号序列,每组数据占一行。若有多个序列满足要求,则输出字典序最小的序列。
Sample Input
3
5 1
4 2
2 0
Sample Output
1 2 3 5 4
1 3 4 2
题目大意:给一个N个自然数(1-N),要求找出逆序对数为K的最小字典序排列的那一个排列方式
解题思路:想要最小字典序那么前面的数字就尽量少的向后面去,因此先计算出满足K个逆序数最少需要LMMN位数字(也就是后LMMN要调动) ②\又因为剩下的数字第一位要尽量小,所以剩下的LMNN-1个数必然倒序排列。③\又因为后LMMN-1个数倒序排列有NXN=(LMMN-1)*(LMMN-2)/2个逆序数,所以剩下数字的第一位的逆序数为K-NXN ④\所以可以确定剩下数字的排列方式。
1 #include<iostream> 2 #include<algorithm> 3 #include<cmath> 4 using namespace std; 5 int getLastMostMoveNum(int k){ 6 return (int)ceil((1.0+sqrt(1.0+8*k))/2); 7 } 8 int getNumOfNiXu(int k){ 9 return k*(k-1)/2; 10 } 11 int main(){ 12 int T;cin>>T; 13 while(T--){ 14 int N,K,i; 15 cin>>N>>K; 16 if(K==0){//顺序输出即可 17 for(i=1;i<N;i++) 18 cout<<i<<' '; 19 cout<<N<<'\n'; 20 }else{//存在逆序对 21 int LMMN=getLastMostMoveNum(K);//计算后LMMN位要变化顺序 22 for(i=1;i<=N-LMMN;i++)//输出前面不用调序的序列 23 cout<<i<<' '; 24 int Last[100005];//保存剩下的数字 25 for(int j=0;i<=N;j++,i++)Last[j]=i; 26 int NXN=getNumOfNiXu(LMMN-1);//计算LMMN-1个数完全逆序的逆序数NXN 27 //所以要用后LMMN位组成K个逆序数就要把Last[K-NXN]放到第一位,其他完全倒序 28 cout<<Last[K-NXN]; 29 for(int j=LMMN-1;j>=0;j--)if(j!=K-NXN)cout<<' '<<Last[j]; 30 cout<<'\n'; 31 } 32 }return 0; 33 }