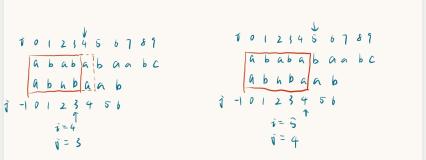在介绍KMP算法之前,先介绍一下BF算法。
BF算法
BF算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。
举例说明:
S: ababcababa
P: ababa
BF算法匹配的步骤如下
KMP算法
在介绍KMP算法之前,先介绍一下BF算法。
一.BF算法
BF算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。
举例说明:
S: ababcababa
P: ababa
BF算法匹配的步骤如下
int BFMatch(char *s,char *p) { int i,j; i=0; while(i<strlen(s)) { j=0; while(s[i]==p[j]&&j<strlen(p)) { i++; j++; } if(j==strlen(p)) return i-strlen(p); i=i-j+1; //指针i回溯 } return -1; }
其实在上面的匹配过程中,有很多比较是多余的。在第五趟匹配失败的时候,在第六趟,i可以保持不变,j值为2。因为在前面匹配的过程中,对于串S,已知s0s1s2s3=p0p1p2p3,又因为p0!=p1!,所以第六趟的匹配是多余的。又由于p0==p2,p1==p3,所以第七趟和第八趟的匹配也是多余的。在KMP算法中就省略了这些多余的匹配。
KMP算法
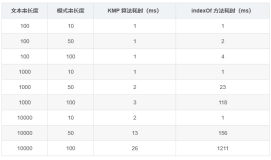
其实KMP算法与BF算法的区别就在于KMP算法巧妙的消除了指针i的回溯问题,只需确定下次匹配j的位置即可,使得问题的复杂度由O(mn)下降到O(m+n)。
在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引入了next[]数组,next[j]的值表示P[0...j-1]中最长后缀的长度等于相同字符序列的前缀。
对于next[]数组的定义如下:
1) next[j] = -1 j = 0
2) next[j] = max(k): 0<k<j P[0...k-1]=P[j-k,j-1]
3) next[j] = 0 其他
如:
P a b a b a
j 0 1 2 3 4
next -1 0 0 1 2
即next[j]=k>0时,表示P[0...k-1]=P[j-k,j-1]
因此KMP算法的思想就是:在匹配过程称,若发生不匹配的情况,如果next[j]>=0,则目标串的指针i不变,将模式串的指针j移动到next[j]的位置继续进行匹配;若next[j]=-1,则将i右移1位,并将j置0,继续进行比较。
代码实现如下:
int KMPMatch(char *s,char *p) { int next[100]; int i,j; i=0; j=0; getNext(p,next); while(i<strlen(s)) { if(j==-1||s[i]==p[j]) { i++; j++; } else { j=next[j]; //消除了指针i的回溯 } if(j==strlen(p)) return i-strlen(p); } return -1; }
因此KMP算法的关键在于求算next[]数组的值,即求算模式串每个位置处的最长后缀与前缀相同的长度, 而求算next[]数组的值有两种思路,第一种思路是用递推的思想去求算,还有一种就是直接去求解。
- 按照递推的思想:
根据定义next[0]=-1,假设next[j]=k, 即P[0...k-1]==P[j-k,j-1]
1)若P[j]==P[k],则有P[0..k]==P[j-k,j],很显然,next[j+1]=next[j]+1=k+1;
2)若P[j]!=P[k],则可以把其看做模式匹配的问题,即匹配失败的时候,k值如何移动,显然k=next[k]。
因此可以这样去实现:
void getNext(char *p,int *next) { int j,k; next[0]=-1; j=0; k=-1; while(j<strlen(p)-1) { if(k==-1||p[j]==p[k]) //匹配的情况下,p[j]==p[k] { j++; k++; next[j]=k; } else //p[j]!=p[k] k=next[k]; } }
- 直接求解方法
void getNext(char *p,int *next) { int i,j,temp; for(i=0;i<strlen(p);i++) { if(i==0) { next[i]=-1; //next[0]=-1 } else if(i==1) { next[i]=0; //next[1]=0 } else { temp=i-1; for(j=temp;j>0;j--) { if(equals(p,i,j)) { next[i]=j; //找到最大的k值 break; } } if(j==0) next[i]=0; } } } bool equals(char *p,int i,int j) //判断p[0...j-1]与p[i-j...i-1]是否相等 { int k=0; int s=i-j; for(;k<=j-1&&s<=i-1;k++,s++) { if(p[k]!=p[s]) return false; } return true; }
Java
/** * Java实现KMP算法 * * 思想:每当一趟匹配过程中出现字符比较不等,不需要回溯i指针, * 而是利用已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远 * 的一段距离后,继续进行比较。 * * 时间复杂度O(n+m) * */ public class KMPTest { public static void main(String[] args) { String s = "abbabbbbcab"; // 主串 String t = "bbcab"; // 模式串 char[] ss = s.toCharArray(); char[] tt = t.toCharArray(); System.out.println(KMP_Index(ss, tt)); // KMP匹配字符串 } /** * 获得字符串的next函数值 * * @param t * 字符串 * @return next函数值 */ public static int[] next(char[] t) { int[] next = new int[t.length]; next[0] = -1; int i = 0; int j = -1; while (i < t.length - 1) { if (j == -1 || t[i] == t[j]) { i++; j++; if (t[i] != t[j]) { next[i] = j; } else { next[i] = next[j]; } } else { j = next[j]; } } return next; } /** * KMP匹配字符串 * * @param s * 主串 * @param t * 模式串 * @return 若匹配成功,返回下标,否则返回-1 */ public static int KMP_Index(char[] s, char[] t) { int[] next = next(t); int i = 0; int j = 0; while (i <= s.length - 1 && j <= t.length - 1) { if (j == -1 || s[i] == t[j]) { i++; j++; } else { j = next[j]; } } if (j < t.length) { return -1; } else return i - t.length; // 返回模式串在主串中的头下标 } }
code(C++)
#include <iostream> #include <cstring> #include <cstdio> using namespace std; int main() { char t[10050],s[1000007]; int c;scanf("%d",&c); while(c--) { scanf("%s%s",t,s); int flink[10004]={}; int i=0,j=-1; flink[0]=-1; int len=strlen(t); while(i<len) { if(j==-1 || t[i]==t[j]) flink[++i]=++j; else j=flink[j]; } int ans=0; i=j=0; int n=len; len=strlen(s); while(i<len) { if(j==-1 || s[i]==t[j]) { ++i;++j; } else { j=flink[j]; } if(j==n) ans++; } printf("%d\n",ans); } return 0; }