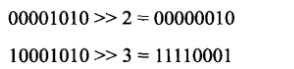求二进制中1的个数
在《编程之美》一书中有一节提到如何求一个字节的无符号整型变量二进制表示中中1的个数,主要提到了四种方法。下面简单介绍一下:
1.求余法
在将十进制数转换为二进制数时,采用除2取余法。将每次除2得到的余数保存起来逆序输出便是该十进制整数的二进制表示。因此可以采用这种方法去统计1的个数。
int count(unsigned char n)
{
int sum=0;
while(n)
{
if(n%2==1)
sum++;
n/=2;
}
return sum;
}
2.位运算
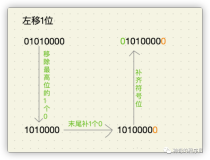
我们知道计算机在处理位运算时速度要快很多,因此可以考虑用位运算的方法来实现。每次先与0X01进行与操作,若非0,则计数器加1,然后向右移1位,循环这个过程。
int count(unsigned char n)
{
int sum=0;
while(n)
{
sum+=n&0x01;
n>>=1;
}
return sum;
}
3.快速法
2中所述方法的循环次数始终为8,有一种方法可以减少这个循环次数。就是采用减1再进行与的运算,这样每进行一次,就会少一个1.
比如: 0010 0110 减1得 0010 0101 &0010 0110等于0010 0100.原因在于比如r1r2...rn,如果最后面位1的一位为rk,则该数减1之后二进制的表示形式中rk肯定为0,但是r(k+1)...rn则全部为1,与原来的数进行与操作不会印象到rk前面的1的个数,因此每进行一次,则可以消去一个二进制1。
int count(unsigned char n)
{
int sum=0;
while(n)
{
n&=(n-1);
sum++;
}
return sum;
}
4.查表法。
因此一个字节的无符号整型数据范围就在[0,255]之间,因此可以直接定义一个长度为256的数组table[0-255],把0-255二进制表示中1的1的个数赋给数组的元素,这样直接进行查找。
int table[256]={
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8,
};
int count(unsigned char n)
{
return table[n];
}
以上是四种不同的方法,如果要求一个32位的无符号整数中含有1的个数,则可以根据第四种方法变换一下:
int table[256]={
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8,
};
int count(unsigned int n)
{
unsigned char *p=(unsigned char *)&n;
return table[*p]+table[*(p+1)]+table[*(p+2)]+table[*(p+3)];
}