1 可测函数
1.1可测函数与简单函数的关系
$$\beex \bea f\mbox{ 非负可测}&\ra \exists\ 0\leq \phi_k\nearrow f,\\ f\mbox{ 有界可测}&\ra \exists\ \phi_k\rightrightarrows f,\\ f\mbox{ 一般可测}&\ra \exists\ \phi_k\to f. \eea \eeex$$ 简言之, 非负可测 $\ra$ 递增逼近; 有界可测 $\ra$ 一致逼近; 一般可测 $\ra$ 点态逼近.
1.2 可测函数与连续函数的关系 (Lusin 定理)
$$\bex f\ae\mbox{ 有限, 可测}\ra \forall\ \delta>0,\ \exists\ F\subset E,\ m(E\bs F)<\delta, f|_F\mbox{ 连续}. \eex$$ 简言之, $f\ae$ 有限, 可测 $\ra$ $f$ 基本上连续.
1.3 可测函数的各种收敛
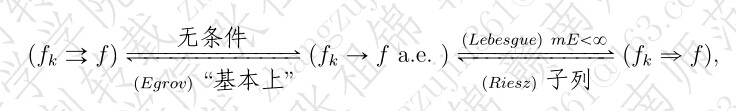 其中,
其中,
(1) Egrov 定理: $$\bex \serd{\ba{ll} mE<\infty\\ f_k\ae\mbox{ 收敛于 }f \ea}\ra f_k\mbox{ 基本上一致收敛于 }f. \eex$$
(2) Lebesgue 定理: $$\bex \serd{\ba{ll} mE<\infty\\ f_k\ae\mbox{ 收敛于 }f \ea}\ra (f_k\ra f). \eex$$
(3) Riesz 定理: $$\bex (f_k\ra f)\ra \exists\ \sed{k_j},\st f_{k_j}\ae\mbox{ 收敛于 }f. \eex$$
2 Lebesgue 积分
2.1 非负可测函数的积分
(1) Levi 定理: $$\bex 0\leq f_k\nearrow f\ra \int \lim f_k=\lim \int f_k. \eex$$
(2) 逐项积分: $$\bex 0\leq f_k\ra \int_E \sum f_k=\sum \int_E f_k. \eex$$
(3) Fatou 引理: $$\bex 0\leq f_k\ra \int_E\varliminf f_k\leq \varliminf \int_E f_k. \eex$$
(4) Fubini 定理: $$\bex 0\leq f\ra \int_{A\times B}f=\int_A\int_B f. \eex$$
2.2 一般可测函数的积分
(1) 积分的绝对连续性 (AC): $$\bex f\in L(E)\ra {\forall\ \ve>0,\ \exists\ \delta>0,\ \forall\ A\subset E: mA<\delta,\atop\mbox{ 有 }\sev{\int_A f(x)\rd x} \leq \int_A|f(x)|\rd x<\ve.} \eex$$
(2) Lebesgue 控制收敛: $$\bex \serd{\ba{ll} |f_i|\leq F,\quad F\in L(E)\\ f_i\to f,\ae\mbox{ 于 }E \ea}\ra\sedd{\ba{ll} \lim_{i\to\infty}\int_E|f_i(x)-f(x)|\rd x=0\\ \lim_{i\to\infty}\int_E f_i(x)\rd x =\int_E f(x)\rd x. \ea} \eex$$
(3) 依测度控制收敛: $$\bex \serd{\ba{ll} |f_i|\leq F,\quad F\in L(E)\\ f_i\ra f \ea}\ra\sedd{\ba{ll} \lim_{i\to\infty}\int_E|f_i(x)-f(x)|\rd x=0\\ \lim_{i\to\infty}\int_E f_i(x)\rd x =\int_E f(x)\rd x. \ea} \eex$$
(4) 逐项积分:$$\bex \serd{\ba{ll} f_i\in L(E)\\ \sum_{i=1}^\infty \int_E|f_i(x)|\rd x<+\infty \ea}\ra\sedd{\ba{ll} \sum_{i=1}^\infty f_i(x),\ae \mbox{ 收敛, 于 }E\\ \int_E\sum_{i=1}^\infty f_i(x)\rd x =\sum_{i=1}^\infty \int_Ef_i(x)\rd x. \ea} \eex$$
(5) 积分号下求导: 设 $f(x,t)$ 是 $E\times (a,b)$ 上的实函数, 则 $$\bex \serd{\ba{ll} f(\cdot,t)\in L(E),\quad \forall\ t\\ f(x,\cdot)\mbox{ 可导}, \sev{\frac{\p f}{\p t}(x,\cdot)}\leq F(x),\ae\mbox{ 于 }E,\quad F\in L(E) \ea}\\ \ra \frac{\rd}{\rd t}\int_E f(x,t)\rd x =\int_E \frac{\p}{\p t}f(x,t)\rd x. \eex$$
(6) Fubini 定理: $$\bex f\in L(A\times B)\ra \int_{A\times B}f=\int_A\int_Bf. \eex$$
2.3 Lebesgue 积分与 Riemann 积分的关系
$$\bex R[a,b]\subset L[a,b],\quad R^+[a,\infty)\subset L^+[a,+\infty). \eex$$
附言
若需更详细的, 请参阅 《家里蹲大学数学杂志第4卷第253期, 实变函数讲义》.



