在大学的时候,应该在数据结构里面都看过kmp算法吧,不知道有多少老师对该算法是一笔带过的,至少我们以前是的,
确实kmp算法还是有点饶人的,如果说红黑树是变态级的,那么kmp算法比红黑树还要变态,很抱歉,每次打kmp的时候,输
入法总是提示“看毛片”三个字,嘿嘿,就叫“看毛片算法”吧。
一:BF算法
如果让你写字符串的模式匹配,你可能会很快的写出朴素的bf算法,至少问题是解决了,我想大家很清楚的知道它的时间复
杂度为O(MN),原因很简单,主串和模式串失配的时候,我们总是将模式串的第一位与主串的下一个字符进行比较,所以复杂
度高在主串每次失配的时候都要回溯,图我就省略了。
二:KMP算法
刚才我们也说了,主串每次都要回溯,从而提高了时间复杂度,那么能不能在“主串”和“模式串”失配的情况下,主串不回溯呢?
而是让”模式串“向右滑动一定的距离,对上号后继续进行下一轮的匹配,从而做到时间复杂度为O(M+N)呢?所以kmp算法就是
用来处理这件事情的,下面我们看下简单的例子。
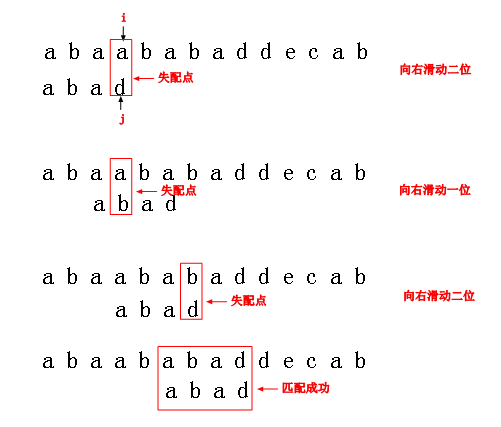
通过这张图,我们来讨论下它的一般推理,假设主串为S,模式串为P,在Si != Pj的时候,我们可以看到满足如下关系式
Si-jSi-j+1...Sn-1=P0P1..Pj-1。那么模式P应该向右滑动多少距离?也就是主串中的第i个字符应与模式串中的哪一个字符进行比较?
假设应该与模式串中的第k的位置相比较,假如模式串中存在最大的前缀真子串和后缀真子串,那么有P0P1..Pk-1=Pj-kPj-k+1...Pj-1.
这句话的意思也就是说,在模式P中,前k个字符与j个字符之前的k个字符相同,比如说:“abad”的最大前缀真子串为“aba",最大
后缀真子串为“bad”,当然这里是不相等,这里的0<k<j,我们希望k接近于j,那么我们滑动的距离将会最小,好吧,现在我们用
next[j]来记录失配时模式串应该用哪一个字符于Si进行比较。
设 next[j]=k。根据公式我们有
-1 当j=0时
next[j] = max{k| 0<k<j 且 P0P1..Pk-1=Pj-kPj-k+1...Pj-1}
0 其他情况
好,接下来的问题就是如何求出next[j],这个也就是kmp思想的核心,对于next[j]的求法,我们采用递推法,现在我们知道了
next[j]=k,我们来求next[j+1]=?的问题?其实也就是两种情况:
①:Pk=Pj 时 则P0P1...Pk=Pj-kPj-k+1...Pj, 则我们知:
next[j+1]=k+1。
又因为next[j]=k,则
next[j+1]=next[j]+1。
②:Pk!=Pj 时 则P0P1...Pk!=Pj-kPj-k+1...Pj,这种情况我们有点蛋疼,其实这里我们又将模式串的匹配问题转化为了上面我们提到
的”主串“和”模式串“中寻找next的问题,你可以理解成在模式串的前缀串和后缀串中寻找next[j]的问题。现在我们的思路就是一定
要找到这个k2,使得Pk2=Pj,然后将k2代入①就可以了。
设 k2=next[k]。 则有P0P1...Pk2-1=Pj-k2Pj-k2+1...Pj-1。
若 Pj=Pk2, 则 next[j+1]=k2+1=next[k]+1。
若 Pj!=Pk2, 则可以继续像上面递归的使用next,直到不存在k2为止。
好,下面我们上代码,可能有点绕,不管你懂没懂,反正我懂了。
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 6 namespace SupportCenter.Test 7 { 8 public class Program 9 { 10 static void Main(string[] args) 11 { 12 string zstr = "ababcabababdc"; 13 14 string mstr = "babdc"; 15 16 var index = KMP(zstr, mstr); 17 18 if (index == -1) 19 Console.WriteLine("没有匹配的字符串!"); 20 else 21 Console.WriteLine("哈哈,找到字符啦,位置为:" + index); 22 23 Console.Read(); 24 } 25 26 static int KMP(string bigstr, string smallstr) 27 { 28 int i = 0; 29 int j = 0; 30 31 //计算“前缀串”和“后缀串“的next 32 int[] next = GetNextVal(smallstr); 33 34 while (i < bigstr.Length && j < smallstr.Length) 35 { 36 if (j == -1 || bigstr[i] == smallstr[j]) 37 { 38 i++; 39 j++; 40 } 41 else 42 { 43 j = next[j]; 44 } 45 } 46 47 if (j == smallstr.Length) 48 return i - smallstr.Length; 49 50 return -1; 51 } 52 53 /// <summary> 54 /// p0,p1....pk-1 (前缀串) 55 /// pj-k,pj-k+1....pj-1 (后缀串) 56 /// </summary> 57 /// <param name="match"></param> 58 /// <returns></returns> 59 static int[] GetNextVal(string smallstr) 60 { 61 //前缀串起始位置("-1"是方便计算) 62 int k = -1; 63 64 //后缀串起始位置("-1"是方便计算) 65 int j = 0; 66 67 int[] next = new int[smallstr.Length]; 68 69 //根据公式: j=0时,next[j]=-1 70 next[j] = -1; 71 72 while (j < smallstr.Length - 1) 73 { 74 if (k == -1 || smallstr[k] == smallstr[j]) 75 { 76 //pk=pj的情况: next[j+1]=k+1 => next[j+1]=next[j]+1 77 next[++j] = ++k; 78 } 79 else 80 { 81 //pk != pj 的情况:我们递推 k=next[k]; 82 //要么找到,要么k=-1中止 83 k = next[k]; 84 } 85 } 86 87 return next; 88 } 89 } 90 }