摘要:
本实验采用遗传算法实现了旅行商问题的模拟求解,并在同等规模问题上用最小生成树算法做了一定的对比工作。遗传算法在计算时间和占用内存上,都远远优于最小生成树算法。
程序采用Microsoft visual studio 2008 结合MFC基本对话框类库开发。32位windows 7系统下调试运行。
引言
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,由密歇根大学的约翰•霍兰德和他的同事于二十世纪六十年代在对细胞自动机(英文:cellular automata)进行研究时率先提出, 并于1975年出版了颇有影响的专著《Adaptation in Natural and Artificial Systems》,GA这个名称才逐渐为人所知,约翰•霍兰德教授所提出的GA通常为简单遗传算法(SGA)。在二十世纪八十年代中期之前,对于遗传算法的研究还仅仅限于理论方面,直到在伊利诺伊大学召开了第一届世界遗传算法大会。随着计算机计算能力的发展和实际应用需求的增多,遗传算法逐渐进入实际应用阶段。1989年,纽约时报作者约翰•马科夫写了一篇文章描述第一个商业用途的遗传算法--进化者(英文:Evolver)。之后,越来越多种类的遗传算法出现并被用于许多领域中,财富杂志500强企业中大多数都用它进行时间表安排、数据分析、未来趋势预测、预算、以及解决很多其他组合优化问题。
遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解[1]。
遗传算法是借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的。其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。遗传算法的这些性质,已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。它是现代有关智能计算中的关键技术。
综述:
程序总体流程图:
这个程序的思想是,随机生成“地点数”编辑框输入的数字的地点,存储在一个vector里。然后用一个“基因类”表示该基因代表第几个点,接着一个“基因组类”有序包含了很多“基因类”,如果一个“基因组类”包含的基因类顺序为:基因组.基因[0].data = 第二个点;基因组.基因[1].data = 第三个点;基因组.基因[3].data = 第一个点;就说明该基因组表示的连线顺序是从第二点连到第三个点再连到第一个点。给每个城市一个固定的基因编号,例如10个城市为 0 1 2 3 4 5 6 7 8 9 ,随机地组成一个染色体(以下所有情况都以10个城市为例说明)。约定这10个城市之间的行走路线为:
(其余基因序列的路线同样道理)
接着有一个“遗传机器类”包含了很多基因组。基因组的数量由“基因组数”编辑框决定。初始化的时候,每个基因组的基因顺序是随机决定的。进行第一代进化的时候,遍历vector<基因组>,计算每个基因组代表的连线方式的连线长度。连线长度越长,说明这个基因组越差劲,因为我们要计算以何种方式连线连线长度最短。
我们用不适应度来记录连线长度。接着就是选择哪个基因组可以生育,遗传给下一代。我采用了一个轮盘赌的策略,尽可能选择不适应度低的基因组进行生育。选择出的基因组进行交换变异后,就把这个基因组复制给下一代。
最后,选择两个最好的基因组,不进行任何变异,直接复制到下一代。这样循环反复,迭代“代数”编辑框输入的代数次数之后,就可以输出结果了。
结果就是最后一代最优秀的那个基因组代表的连线方式。
主要代码:
void cGAMachine::SetupNextGeneration()//生成下一代基因,进化到下一代
{
vector<cGenome> offspring;//保存下一代基因
m_maxNotFitness = m_genomes[m_population - 1].m_notfitness;
//所有基因组最大不适应度
while (offspring.size() < (unsigned int)m_population - 2)
//选择(最大基因组数-2)数量的基因组进行变异和遗传
{
cGenome parent = SelectRouletteWheel();
//进行轮盘赌随机选择一个基因组出来进行生育
cGenome offspring1;
//保存变异后的基因组
MutateInsert(parent.m_genes, offspring1.m_genes);//进行变异
offspring.push_back(offspring1);
//将变异后的基因组压入第二代vector<基因组>里
}
sort(m_genomes.begin(), m_genomes.end());
//对vector<基因组>进行排序,以便下一行代码选出最优秀的个基因组
CopyEliteInto(offspring);
//直接将最优秀的个基因组复制到下一代
m_genomes = offspring;
m_curGener++;//代数计数器+1
}
cGenome& cGAMachine::SelectRouletteWheel()
{
int nRand = rand() % (int)(m_crossOverRate * m_maxNotFitness) + 0.5 * m_maxNotFitness;
for (std::vector<cGenome>::iterator iter = m_genomes.begin(); iter != m_genomes.end(); ++iter)
{
if (iter->m_notfitness <= nRand)
{
return *iter;
break;
}
}
return m_genomes[0];
}
void cGAMachine::MutateInsert(const vector<cGene> &parent, vector<cGene> &offspring)//插入变异
{
if ((rand() / (double)(RAND_MAX)) > m_mutationRate)
{
offspring = parent;
return;
}
int nRandscr = rand() % (parent.size() - 1);
int nRanddes = rand() % (parent.size() - 1);
if (nRanddes == nRandscr)
{
offspring = parent;
return;
}
cGene geneInsert = parent[nRandscr];
cGene geneDes = parent[nRanddes];
offspring = parent;
offspring.erase(offspring.begin() + nRandscr);
if (nRandscr < nRanddes)
{
offspring.erase(offspring.begin() + nRanddes - 1);
offspring.insert(offspring.begin() + nRanddes - 1, geneInsert);
offspring.insert(offspring.begin() + nRandscr, geneDes);
}
else
{
offspring.erase(offspring.begin() + nRanddes);
offspring.insert(offspring.begin() + nRanddes, geneInsert);
offspring.insert(offspring.begin() + nRandscr, geneDes);
}
}
void cGAMachine::CopyEliteInto(std::vector<cGenome> &offspring)
{
for (int i = 0; i < 2 && i < m_population; i++)
{
offspring.push_back(m_genomes[i]);
}
}
cGenome& cGAMachine::GetBestResult()
{
sort(m_genomes.begin(), m_genomes.end());
return m_genomes[0];
}
实验结果:
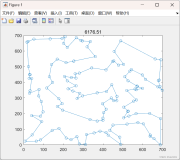
使用上图随机生成的节点采用最小生成树
采用50个基因组,100次迭代进化,0.5的基因变异率
依次生成50个点,100个点,150个点,200个点,250个点的规模问题运行时间的对比:release版本程序
随着节点数的增加遗传算法的运行时间基本保持在100ms左右
占用内存对比:
发现的问题:
1. 虽然遗传算法在性能上优势很大,但是有时候基本是收敛在局部最优解上了,找全局最优解需要改进的遗传算法。
2. 每次发现的解有很大的不确定性,看人品的算法。
未来的工作:
1. 参照《最小生成树算法在旅行商问题中的应用》实现最小生成树的TSP解法法。
2. 改进遗传算法,引入灾变的思想,得到全局最优解。
3. 进一步了解其他智能算法的TSP问题解决方案
参考文献:
1.
2.
3. http://blog.csdn.net/corivsky/article/details/3621415
工程代码下载地址:
http://download.csdn.net/detail/wangyaninglm/6705587
其他算法:
//=====================================================================
//基本蚁群算法源代码
//使用的城市数据是eil51.tsp
//=====================================================================
// AO.cpp : 定义控制台应用程序的入口点。
#pragma once
#include <iostream>
#include <math.h>
#include <time.h>
//=====================================================================
//常量定义和参数定义
//=====================================================================
const double ALPHA=1.0; //启发因子,信息素的重要程度
const double BETA=2.0; //期望因子,城市间距离的重要程度
const double ROU=0.5; //信息素残留参数
const int N_ANT_COUNT=34; //蚂蚁数量
const int N_IT_COUNT=1000; //迭代次数
const int N_CITY_COUNT=51; //城市数量
const double DBQ=100.0; //总的信息素
const double DB_MAX=10e9; //一个标志数,10的9次方
double g_Trial[N_CITY_COUNT][N_CITY_COUNT]; //两两城市间信息素,就是环境信息素
double g_Distance[N_CITY_COUNT][N_CITY_COUNT]; //两两城市间距离
//eil51.tsp城市坐标数据
double x_Ary[N_CITY_COUNT]=
{
37,49,52,20,40,21,17,31,52,51,
42,31,5,12,36,52,27,17,13,57,
62,42,16,8,7,27,30,43,58,58,
37,38,46,61,62,63,32,45,59,5,
10,21,5,30,39,32,25,25,48,56,
30
};
double y_Ary[N_CITY_COUNT]=
{
52,49,64,26,30,47,63,62,33,21,
41,32,25,42,16,41,23,33,13,58,
42,57,57,52,38,68,48,67,48,27,
69,46,10,33,63,69,22,35,15,6,
17,10,64,15,10,39,32,55,28,37,
40
};
//返回指定范围内的随机整数
int rnd(int nLow,int nUpper)
{
return nLow+(nUpper-nLow)*rand()/(RAND_MAX+1);
}
//返回指定范围内的随机浮点数
double rnd(double dbLow,double dbUpper)
{
double dbTemp=rand()/((double)RAND_MAX+1.0);
return dbLow+dbTemp*(dbUpper-dbLow);
}
//返回浮点数四舍五入取整后的浮点数
double ROUND(double dbA)
{
return (double)((int)(dbA+0.5));
}
//=====================================================================
//蚂蚁类的定义和实现
//=====================================================================
//定义蚂蚁类
class CAnt
{
public:
CAnt(void);
~CAnt(void);
public:
int m_nPath[N_CITY_COUNT]; //蚂蚁走的路径
double m_dbPathLength; //蚂蚁走过的路径长度
int m_nAllowedCity[N_CITY_COUNT]; //没去过的城市
int m_nCurCityNo; //当前所在城市编号
int m_nMovedCityCount; //已经去过的城市数量
public:
int ChooseNextCity(); //选择下一个城市
void Init(); //初始化
void Move(); //蚂蚁在城市间移动
void Search(); //搜索路径
void CalPathLength(); //计算蚂蚁走过的路径长度
};
//构造函数
CAnt::CAnt(void)
{
}
//析构函数
CAnt::~CAnt(void)
{
}
//初始化函数,蚂蚁搜索前调用
void CAnt::Init()
{
for (int i=0;i<N_CITY_COUNT;i++)
{
m_nAllowedCity=1; //设置全部城市为没有去过
m_nPath=0; //蚂蚁走的路径全部设置为0
}
//蚂蚁走过的路径长度设置为0
m_dbPathLength=0.0;
//随机选择一个出发城市
m_nCurCityNo=rnd(0,N_CITY_COUNT);
//把出发城市保存入路径数组中
m_nPath[0]=m_nCurCityNo;
//标识出发城市为已经去过了
m_nAllowedCity[m_nCurCityNo]=0;
//已经去过的城市数量设置为1
m_nMovedCityCount=1;
}
//选择下一个城市
//返回值 为城市编号
int CAnt::ChooseNextCity()
{
int nSelectedCity=-1; //返回结果,先暂时把其设置为-1
//==============================================================================
//计算当前城市和没去过的城市之间的信息素总和
double dbTotal=0.0;
double prob[N_CITY_COUNT]; //保存各个城市被选中的概率
for (int i=0;i<N_CITY_COUNT;i++)
{
if (m_nAllowedCity == 1) //城市没去过
{
//该城市和当前城市间的信息素
prob=pow(g_Trial[m_nCurCityNo],ALPHA)*pow(1.0/g_Distance[m_nCurCityNo],BETA);
dbTotal=dbTotal+prob; //累加信息素,得到总和
}
else //如果城市去过了,则其被选中的概率值为0
{
prob=0.0;
}
}
//==============================================================================
//进行轮盘选择
double dbTemp=0.0;
if (dbTotal > 0.0) //总的信息素值大于0
{
dbTemp=rnd(0.0,dbTotal); //取一个随机数
for (int i=0;i<N_CITY_COUNT;i++)
{
if (m_nAllowedCity == 1) //城市没去过
{
dbTemp=dbTemp-prob; //这个操作相当于转动轮盘,如果对轮盘选择不熟悉,仔细考虑一下
if (dbTemp < 0.0) //轮盘停止转动,记下城市编号,直接跳出循环
{
nSelectedCity=i;
break;
}
}
}
}
//==============================================================================
//如果城市间的信息素非常小 ( 小到比double能够表示的最小的数字还要小 )
//那么由于浮点运算的误差原因,上面计算的概率总和可能为0
//会出现经过上述操作,没有城市被选择出来
//出现这种情况,就把第一个没去过的城市作为返回结果
if (nSelectedCity == -1)
{
for (int i=0;i<N_CITY_COUNT;i++)
{
if (m_nAllowedCity == 1) //城市没去过
{
nSelectedCity=i;
break;
}
}
}
//==============================================================================
//返回结果,就是城市的编号
return nSelectedCity;
}
//蚂蚁在城市间移动
void CAnt::Move()
{
int nCityNo=ChooseNextCity(); //选择下一个城市
m_nPath[m_nMovedCityCount]=nCityNo; //保存蚂蚁走的路径
m_nAllowedCity[nCityNo]=0;//把这个城市设置成已经去过了
m_nCurCityNo=nCityNo; //改变当前所在城市为选择的城市
m_nMovedCityCount++; //已经去过的城市数量加1
}
//蚂蚁进行搜索一次
void CAnt::Search()
{
Init(); //蚂蚁搜索前,先初始化
//如果蚂蚁去过的城市数量小于城市数量,就继续移动
while (m_nMovedCityCount < N_CITY_COUNT)
{
Move();
}
//完成搜索后计算走过的路径长度
CalPathLength();
}
//计算蚂蚁走过的路径长度
void CAnt::CalPathLength()
{
m_dbPathLength=0.0; //先把路径长度置0
int m=0;
int n=0;
for (int i=1;i<N_CITY_COUNT;i++)
{
m=m_nPath;
n=m_nPath[i-1];
m_dbPathLength=m_dbPathLength+g_Distance[m][n];
}
//加上从最后城市返回出发城市的距离
n=m_nPath[0];
m_dbPathLength=m_dbPathLength+g_Distance[m][n];
}
//=====================================================================
//TSP类的定义和实现
//=====================================================================
//tsp类
class CTsp
{
public:
CTsp(void);
~CTsp(void);
public:
CAnt m_cAntAry[N_ANT_COUNT]; //蚂蚁数组
CAnt m_cBestAnt; //定义一个蚂蚁变量,用来保存搜索过程中的最优结果
//该蚂蚁不参与搜索,只是用来保存最优结果
public:
//初始化数据
void InitData();
//开始搜索
void Search();
//更新环境信息素
void UpdateTrial();
};
//构造函数
CTsp::CTsp(void)
{
}
CTsp::~CTsp(void)
{
}
//初始化数据
void CTsp::InitData()
{
//先把最优蚂蚁的路径长度设置成一个很大的值
m_cBestAnt.m_dbPathLength=DB_MAX;
//计算两两城市间距离
double dbTemp=0.0;
for (int i=0;i<N_CITY_COUNT;i++)
{
for (int j=0;j<N_CITY_COUNT;j++)
{
dbTemp=(x_Ary-x_Ary[j])*(x_Ary-x_Ary[j])+(y_Ary-y_Ary[j])*(y_Ary-y_Ary[j]);
dbTemp=pow(dbTemp,0.5);
//城市间距离四舍五入取整,eil51.tsp的最短路径426是距离按四舍五入取整后得到的。
g_Distance[j]=ROUND(dbTemp);
}
}
//初始化环境信息素,先把城市间的信息素设置成一样
//这里设置成1.0,设置成多少对结果影响不是太大,对算法收敛速度有些影响
for (int i=0;i<N_CITY_COUNT;i++)
{
for (int j=0;j<N_CITY_COUNT;j++)
{
g_Trial[j]=1.0;
}
}
}
//更新环境信息素
void CTsp::UpdateTrial()
{
//临时数组,保存各只蚂蚁在两两城市间新留下的信息素
double dbTempAry[N_CITY_COUNT][N_CITY_COUNT];
memset(dbTempAry,0,sizeof(dbTempAry)); //先全部设置为0
//计算新增加的信息素,保存到临时数组里
int m=0;
int n=0;
for (int i=0;i<N_ANT_COUNT;i++) //计算每只蚂蚁留下的信息素
{
for (int j=1;j<N_CITY_COUNT;j++)
{
m=m_cAntAry.m_nPath[j];
n=m_cAntAry.m_nPath[j-1];
dbTempAry[n][m]=dbTempAry[n][m]+DBQ/m_cAntAry.m_dbPathLength;
dbTempAry[m][n]=dbTempAry[n][m];
}
//最后城市和开始城市之间的信息素
n=m_cAntAry.m_nPath[0];
dbTempAry[n][m]=dbTempAry[n][m]+DBQ/m_cAntAry.m_dbPathLength;
dbTempAry[m][n]=dbTempAry[n][m];
}
//==================================================================
//更新环境信息素
for (int i=0;i<N_CITY_COUNT;i++)
{
for (int j=0;j<N_CITY_COUNT;j++)
{
g_Trial[j]=g_Trial[j]*ROU+dbTempAry[j]; //最新的环境信息素 = 留存的信息素 + 新留下的信息素
}
}
}
void CTsp::Search()
{
char cBuf[256]; //打印信息用
//在迭代次数内进行循环
for (int i=0;i<N_IT_COUNT;i++)
{
//每只蚂蚁搜索一遍
for (int j=0;j<N_ANT_COUNT;j++)
{
m_cAntAry[j].Search();
}
//保存最佳结果
for (int j=0;j<N_ANT_COUNT;j++)
{
if (m_cAntAry[j].m_dbPathLength < m_cBestAnt.m_dbPathLength)
{
m_cBestAnt=m_cAntAry[j];
}
}
//更新环境信息素
UpdateTrial();
//输出目前为止找到的最优路径的长度
sprintf(cBuf,"\n[%d] %.0f",i+1,m_cBestAnt.m_dbPathLength);
printf(cBuf);
}
}
//=====================================================================
//主程序
//=====================================================================
int main()
{
//用当前时间点初始化随机种子,防止每次运行的结果都相同
time_t tm;
time(&tm);
unsigned int nSeed=(unsigned int)tm;
srand(nSeed);
//开始搜索
CTsp tsp;
tsp.InitData(); //初始化
tsp.Search(); //开始搜索
//输出结果
printf("\nThe best tour is :\n");
char cBuf[128];
for (int i=0;i<N_CITY_COUNT;i++)
{
sprintf(cBuf,"%02d ",tsp.m_cBestAnt.m_nPath+1);
if (i % 20 == 0)
{
printf("\n");
}
printf(cBuf);
}
printf("\n\nPress any key to exit!");
getchar();
return 0;
}