支持向量机分类实战-阿里云开发者社区

更多深度文章，请关注云计算频道：https://yq.aliyun.com/cloud

支持向量机（SVM）是一个非常强大和灵活的机器学习模型，能够执行线性或非线性的分类，回归，甚至异常值检测。它是机器学习中最受欢迎的有监督学习模式之一，任何对ML感兴趣的人都应该对其有所了解，并且能够掌握其使用方法。SVM特别适用于复杂但数据集属于中小型的分类。

SVM主要的思想可以概括为两点：

1，它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。

2，它基于结构风险最小化理论之上在特征空间中构建最优超平面，使得学习器得到全局最优化，并且在整个样本空间的期望以某种概率满足一定上界。

在这篇文章中，我们将探讨如何用Python实现分类的SVM模型。

线性SVM

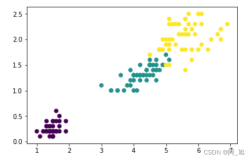
假设我们有两类数据，我们要使用SVM进行分类，如图所示：

这两个类数据可以用直线（线性分离）轻松分离。左图显示了2个可能的线性分类器的决策边界。SVM模型其实就是关于生成正确的分界线（在较高维度称为Hyperplane）。在左图中，我们可以看到数据分类非常好，尽管红线对数据进行了分类，但在新的数据实例中可能无法很好地执行。我们可以画出许多对这些数据进行分类的线，但是在所有这些线中，蓝线可以分隔最多的数据。如果将相同的蓝线显示在右图，这条线（超平面）不仅分离了两个类，而且还保持了最远的相近的训练实例的距离。我们称之为大间距分类器（Large Margin Classification）。

这个最好的决策边界是由位于分界线边缘的实例确定（或“支持”）的。这些实例称为支持向量两条线边缘之间的距离称为边距。

软间距分类器（soft Margin Classification）

如果我们严格把我们所用的例子放在这两条虚线上（如下图），并且在正确的一边，这就是所谓的硬间距分类，硬间距分类有2个问题。

1）只有数据线性分离才有效。

2）对异常值非常敏感。

在上面的数据类中，有一个蓝色的异常值。如果我们对该数据集应用硬间距分类器，我们将获得左边图所示的小边距的决策边界。为了避免这些问题，最好使用更灵活的模型。目的是在保持两条线之间距离尽可能大的情况下找到一个良好的平衡，并限制边际违规（即，最终在两条线中间的距离甚至错误的一面的情况），这称为软间距分类器。如果我们对该数据集应用软间距分类，我们将获得比硬间距分类更大的确定边界，这在右图中显示。

非线性SVM

虽然线性SVM分类器是有效的，并且在许多情况下令人惊奇地工作，但是许多数据集是不能接近线性分离。处理非线性数据集的一个简单方法是添加更多的特征，例如多项式特征，有时这可以导致线性可分离的数据集。通过生成多项式特征，我们将具有一个新特征矩阵，该特征矩阵由具有小于或等于指定度数的特征的所有多项式组合组成。以下图像是使用多项式特征进行SVM的示例。

核心技巧

内核是计算两个向量X，Y的点积的一种方法和在某些（可能非常高的维度）特征空间中，这就是为什么内核函数有时被称为“广义点积分”。假设我们有一个映射：φ:Rn→Rm，这使我们的矢量在Rn到某些特征空间Rm。然后数量积X，Y在这个空间里面是 φ(x)Tφ(y)。一个内核是一个函数K相当于数量积：k(x,y)=φ(x)Tφ(y)。内核提供了一种方法来计算某些特征空间中的点积，甚至不知道这个空间是什么。

多项式内核

添加多项式特征非常简单。但是低度多项式不能处理复杂的数据集，并且具有较高的多项式度将会产生大量的特征，使得模型太慢。在这种情况下，我们可以使用多项式内核来避免这个问题。多项式内核具有以下格式：

这里的D是多项式的次数。

高斯RBF内核

高斯RBF（径向基函数）是SVM模型中使用的另一种流行的内核方法。高斯内核具有以下格式：

k （x，y）= e- γ| x - y |2，γ> 0

如果我们有如下的数据集，则RBF内核非常有用。

超参数

在SVM模型中有2个重要的超参数：

1.C参数

C参数决定SVM分类器的边距宽度，而且它的分类器严格，因此边缘宽度较小。对于值大的C，如果该超平面更好地将所有训练点归类正确，则该模型将选择较小余量的超平面。相反，C的非常小的值将导致模型寻找更大的边缘从而分离超平面。对于非常小的C值，你应该得到错误分类的例子，通常即使你的训练数据是线性分离的。

2.γ参数

这个γ参数定义了每个训练示例，γ参数对于scikit-learning中的线性内核是无效的。

应用scikit实现SVM

在这部分中，我们将使用scikit学习来实现SVM，我们将使用人工数据集。

线性内核：

import numpy as np
import pandas as pd
from matplotlib import style
from sklearn.svm import SVC
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 6)
style.use('ggplot')
# Import Dataset
data = pd.read_csv('data.csv', header=None)
X = data.values[:, :2]
y = data.values[:, 2]
# A function to draw hyperplane and the margin of SVM classifier
def draw_svm(X, y, C=1.0):
    # Plotting the Points
    plt.scatter(X[:,0], X[:,1], c=y)
        # The SVM Model with given C parameter
    clf = SVC(kernel='linear', C=C)
    clf_fit = clf.fit(X, y)
        # Limit of the axes
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
        # Creating the meshgrid
    xx = np.linspace(xlim[0], xlim[1], 200)
    yy = np.linspace(ylim[0], ylim[1], 200)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = clf.decision_function(xy).reshape(XX.shape)
    # Plotting the boundary
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], 
                        alpha=0.5, linestyles=['--', '-', '--'])
    ax.scatter(clf.support_vectors_[:, 0], 
                clf.support_vectors_[:, 1], 
                s=100, linewidth=1, facecolors='none')
    plt.show()
    # Returns the classifier
    return clf_fit
clf_arr = []
clf_arr.append(draw_svm(X, y, 0.0001))
clf_arr.append(draw_svm(X, y, 0.001))
clf_arr.append(draw_svm(X, y, 1))
clf_arr.append(draw_svm(X, y, 10))
for i, clf in enumerate(clf_arr):
    # Accuracy Score
    print(clf.score(X, y))
    pred = clf.predict([(12, 32), (-250, 32), (120, 43)])
    print(pred)
        
          
        
        
        
          
          AI 代码解读

0.992907801418
        
          
        
        
        
          
          AI 代码解读

0.992907801418
        
          
        
        
        
          
          AI 代码解读

[1 0 1]

你可以看到具有不同边距宽度的相同超平面，这取决于C超参数。

多项式内核：

import numpy as np
import pandas as pd
from matplotlib import style
from sklearn.svm import SVC
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 6)
style.use('ggplot')
data = pd.read_csv('polydata2.csv', header=None)
X = data.values[:, :2]
y = data.values[:, 2]
def draw_svm(X, y, C=1.0):
    plt.scatter(X[:,0], X[:,1], c=y)
    clf = SVC(kernel='poly', C=C)
    clf_fit = clf.fit(X, y)
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    xx = np.linspace(xlim[0], xlim[1], 200)
    yy = np.linspace(ylim[0], ylim[1], 200)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = clf.decision_function(xy).reshape(XX.shape)
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], 
                        alpha=0.5, linestyles=['--', '-', '--'])
    ax.scatter(clf.support_vectors_[:, 0], 
                clf.support_vectors_[:, 1], 
                s=100, linewidth=1, facecolors='none')
    plt.show()
    return clf_fit
clf = draw_svm(X, y)
score = clf.score(X, y)
pred = clf.predict([(-130, 110), (-170, -160), (80, 90), (-280, 20)])
print(score)
print(pred)

        
          
        
        
        
          
          AI 代码解读

高斯内核：

import numpy as np
import pandas as pd
from matplotlib import style
from sklearn.svm import SVC
from sklearn.datasets import make_classification, make_blobs, make_moons
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 6)
style.use('ggplot')
X, y = make_moons(n_samples=200)
# Auto gamma equals 1/n_features
def draw_svm(X, y, C=1.0, gamma='auto'):
    plt.scatter(X[:,0], X[:,1], c=y)
    clf = SVC(kernel='rbf', C=C, gamma=gamma)
    clf_fit = clf.fit(X, y)
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    xx = np.linspace(xlim[0], xlim[1], 200)
    yy = np.linspace(ylim[0], ylim[1], 200)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = clf.decision_function(xy).reshape(XX.shape)
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], 
                        alpha=0.5, linestyles=['--', '-', '--'])
    ax.scatter(clf.support_vectors_[:, 0], 
                clf.support_vectors_[:, 1], 
                s=100, linewidth=1, facecolors='none')
    plt.show()
    return clf_fit
clf_arr = []
clf_arr.append(draw_svm(X, y, 0.01))
clf_arr.append(draw_svm(X, y, 0.1))
clf_arr.append(draw_svm(X, y, 1))
clf_arr.append(draw_svm(X, y, 10))
for i, clf in enumerate(clf_arr):
    print(clf.score(X, y))

        
          
        
        
        
          
          AI 代码解读

import numpy as np
import pandas as pd
from matplotlib import style
from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 6)
style.use('ggplot')
X, y = make_gaussian_quantiles(n_samples=200, n_features=2, n_classes=2, cov=3)
# Auto gamma equals 1/n_features
def draw_svm(X, y, C=1.0, gamma='auto'):
    plt.scatter(X[:,0], X[:,1], c=y)
    clf = SVC(kernel='rbf', C=C, gamma=gamma)
    clf_fit = clf.fit(X, y)
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    xx = np.linspace(xlim[0], xlim[1], 200)
    yy = np.linspace(ylim[0], ylim[1], 200)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = clf.decision_function(xy).reshape(XX.shape)
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], 
                        alpha=0.5, linestyles=['--', '-', '--'])
    ax.scatter(clf.support_vectors_[:, 0], 
                clf.support_vectors_[:, 1], 
                s=100, linewidth=1, facecolors='none')
    plt.show()
    return clf_fit
clf_arr = []
clf_arr.append(draw_svm(X, y, 0.1))
clf_arr.append(draw_svm(X, y, 1))
clf_arr.append(draw_svm(X, y, 10))
clf_arr.append(draw_svm(X, y, 100))
for i, clf in enumerate(clf_arr):
    print(clf.score(X, y))

        
          
        
        
        
          
          AI 代码解读

γ参数对RBF SVM模型非常重要。在第一个例子中，γ的低值导致非线性分类几乎接近线性分类。

如果你对此感兴趣，你可以查看此Github Repo代码示例和数据集。

本文由北邮@爱可可-爱生活老师推荐，阿里云云栖社区组织翻译。

文章原标题《Support Vector Machines for Classification》

作者：Mubaris NK

译者：虎说八道，审校。

文章为简译，更为详细的内容，请查看。

支持向量机分类实战

非线性SVM

核心技巧

应用scikit实现SVM

热门文章

最新文章

相关课程

相关电子书

相关实验场景

探索云世界

热门

云计算

大数据

云原生

人工智能

数据库

开发与运维

活动广场

任务中心

训练营

直播

乘风者计划

下载

镜像站

技术资料

支持向量机分类实战

非线性SVM

核心技巧

应用scikit实现SVM

热门文章

最新文章

相关课程

相关电子书

相关实验场景