2.3 设计算法
我们可以选择使用的算法设计技术有很多。插入排序使用了增量方法:在排序子数组A[1..j-1]后,将单个元素A[j]插入子数组的适当位置,产生排序好的子数组A[1..j]。
本节我们考查另一种称为“分治法”的设计方法。第4章将更深入地探究该方法。我们将用分治法来设计一个排序算法,该算法的最坏情况运行时间比插入排序要少得多。分治算法的优点之一是,通过使用第4章介绍的技术往往很容易确定其运行时间。
29
2.3.1 分治法
许多有用的算法在结构上是递归的:为了解决一个给定的问题,算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。这些算法典型地遵循分治法的思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治模式在每层递归时都有三个步骤:
分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
解决这些子问题,递归地求解各子问题。然而,若子问题的规模足够小,则直接求解。
合并这些子问题的解成原问题的解。
归并排序算法完全遵循分治模式。直观上其操作如下:
分解:分解待排序的n个元素的序列成各具n/2个元素的两个子序列。
解决:使用归并排序递归地排序两个子序列。
合并:合并两个已排序的子序列以产生已排序的答案。
当待排序的序列长度为1时,递归“开始回升”,在这种情况下不要做任何工作,因为长度为1的每个序列都已排好序。
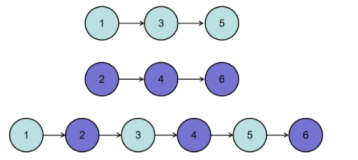
归并排序算法的关键操作是“合并”步骤中两个已排序序列的合并。我们通过调用一个辅助过程MERGE(A,p,q,r)来完成合并,其中A是一个数组,p、q和r是数组下标,满足p≤q<r。该过程假设子数组A[p..q]和A[q+1..r]都已排好序。它合并这两个子数组形成单一的已排好序的子数组并代替当前的子数组A[p..r]。
过程MERGE需要Θ(n)的时间,其中n=r-p+1是待合并元素的总数。它按以下方式工作。回到我们玩扑克牌的例子,假设桌上有两堆牌面朝上的牌,每堆都已排序,最小的牌在顶上。我们希望把这两堆牌合并成单一的排好序的输出堆,牌面朝下地放在桌上。我们的基本步骤包括在牌面朝上的两堆牌的顶上两张牌中选取较小的一张,将该牌从其堆中移开
30(该堆的顶上将显露一张新牌)并牌面朝下地将该牌放置到输出堆。重复这个步骤,直到一个输入堆为空,这时,我们只是拿起剩余的输入堆并牌面朝下地将该堆放置到输出堆。因为我们只是比较顶上的两张牌,所以计算上每个基本步骤需要常量时间。因为我们最多执行n个基本步骤,所以合并需要Θ(n)的时间。
下面的伪代码实现了上面的思想,但有一个额外的变化,以避免在每个基本步骤必须检查是否有堆为空。在每个堆的底部放置一张哨兵牌,它包含一个特殊的值,用于简化代码。这里,我们使用∞作为哨兵值,结果每当显露一张值为∞的牌,它不可能为较小的牌,除非两个堆都已显露出其哨兵牌。但是,一旦发生这种情况,所有非哨兵牌都已被放置到输出堆。因为我们事先知道刚好r-p+1张牌将被放置到输出堆,所以一旦已执行r-p+1个基本步骤,算法就可以停止。


图2-3 当子数组A[9..16]包含序列〈2,4,5,7,1,2,3,6〉时,调用MERGE(A,9,12,16)第10~17行的操作。在复制并插入哨兵后,数组L包含〈2,4,5,7,∞〉,数组R包含〈1,2,3,6,∞〉。A中的浅阴影位置包含它们的最终值,L和R中的浅阴影位置包含有待于被复制回A的值。合在一起,浅阴影位置总是包含原来在A[9..16]中的值和两个哨兵。A中的深阴影位置包含将被覆盖的值,L和R中的深阴影位置包含已被复制回A的值。(a)~(h)在第12~17行循环的每次迭代之前,数组A、L和R以及它们各自的下标k、i和j。(i)终止时的数组与下标。这时,A[9..16]中的子数组已排好序,L和R中的两个哨兵是这两个数组中仅有的两个未被复制回A的元素
过程MERGE的详细工作过程如下:第1行计算子数组A[p..q]的长度n1,第2行计算子数组A[q+1..r]的长度n2。在第3行,我们创建长度分别为n1+1和n2+1的数组L和R(“左”和“右”),每个数组中额外的位置将保存哨兵。第4~5行的for循环将子数组A[p..q]复制到L[1..n1],第6~7行的for循环将子数组A[q+1..r]复制到R[1..n2]。第8~9行将哨兵放在数组L和R的末尾。第10~17行图示在图2-3中,通过维持以下循环不变式,执行r-p+1个基本步骤:
在开始第12~17行for循环的每次迭代时,子数组A[p..k-1]按从小到大的顺序包含L[1..n1+1]和R[1..n2+1]中的k-p个最小元素。进而,L[i]和R[j]是各自所在数组中未被复制回数组A的最小元素。
我们必须证明第12~17行for循环的第一次迭代之前该循环不变式成立,该循环的每次迭代保持该不变式,并且循环终止时,该不变式提供了一种有用的性质来证明正确性。
在第3章中,我们将看到如何形式化地解释包含Θ记号的等式。
表达式x表示大于或等于x的最小整数,x表示小于或等于x的最大整数。这些记号在第3章中定义。验证把q置为(p+r)/2将产生规模分别为n/2和n/2的子数组A[p..q]和A[q+1..r]的最容易的方法是根据p和r为奇数还是偶数分别考查可能出现的4种情况。
初始化:循环的第一次迭代之前,有k=p,所以子数组A[p..k-1]为空。这个空的子数组包含L和R的k-p=0个最小元素。又因为i=j=1,所以L[i]和R[j]都是各自所在数组中未被复制回数组A的最小元素。
保持:为了理解每次迭代都维持循环不变式,首先假设L[i]≤R[j]。这时,L[i]是未被复制回数组A的最小元素。因为A[p..k-1]包含k-p个最小元素,所以在第14行将L[i]复制到A[k]之后,子数组A[p..k]将包含k-p+1个最小元素。增加k的值(在for循环中更新)和i的值(在第15行中)后,为下次迭代重新建立了该循环不变式。反之,若L[i]>R[j],则第16~17行执行适当的操作来维持该循环不变式。
终止:终止时k=r+1。根据循环不变式,子数组A[p..k-1]就是A[p..r]且按从小到大的顺序包含L[1..n1+1]和R[1..n2+1]中的k-p=r-p+1个最小元素。
31
~
33数组L和R一起包含n1+n2+2=r-p+3个元素。除两个最大的元素以外,其他所有元素都已被复制回数组A,这两个最大的元素就是哨兵。
为了理解过程MERGE的运行时间是Θ(n),其中n=r-p+1,注意到,第1~3行和第8~11行中的每行需要常量时间,第4~7行的for循环需要
Θ(n1+n2)=Θ(n)的时间,并且,第12~17行的for循环有n次迭代,每次迭代需要常量时间。
现在我们可以把过程MERGE作为归并排序算法中的一个子程序来用。下面的过程MERGE-SORT(A,p,r)排序子数组A[p..r]中的元素。若p≥r,则该子数组最多有一个元素,所以已经排好序。否则,分解步骤简单地计算一个下标q,将A[p..r]分成两个子数组A[p..q]和A[q+1..r],前者包含n/2个元素,后者包含n/2个元素。
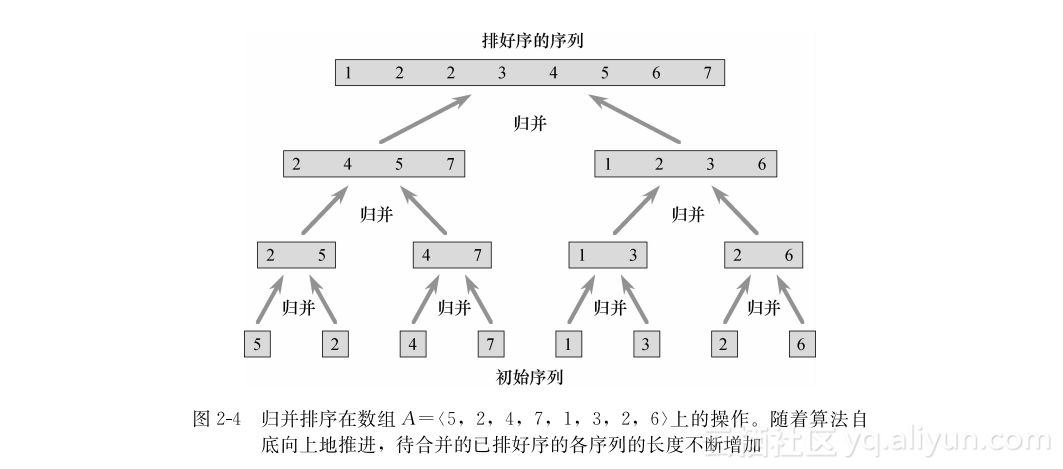
为了排序整个序列A=〈A[1],A[2],…,A[n]〉,我们执行初始调用MERGE-SORT(A,1,A.length),这里再次有A.length=n。图2-4自底向上地说明了当n为2的幂时该过程的操作。算法由以下操作组成:合并只含1项的序列对形成长度为2的排好序的序列,合并长度为2的序列对形成长度为4的排好序的序列,依此下去,直到长度为n/2的两个序列被合并最终形成长度为n的排好序的序列。
2.3.2 分析分治算法
当一个算法包含对其自身的递归调用时,我们往往可以用递归方程或递归式来描述其运行时间,该方程根据在较小输入上的运行时间来描述在规模为n的问题上的总运行时间。然后,我们可以使用数学工具来求解该递归式并给出算法性能的界。
分治算法运行时间的递归式来自基本模式的三个步骤。如前所述,我们假设T(n)是规模为n的一个问题的运行时间。若问题规模足够小,如对某个常量c,n≤c,则直接求解需要常量时间,我们将其写作Θ(1)。假设把原问题分解成a个子问题,每个子问题的规模是原问题的1/b。(对归并排序,a和b都为2,然而,我们将看到在许多分治算法中,a≠b。)为了求解一个规模为n/b的子问题,需要T(n/b)的时间,所以需要aT(n/b)的时间来求解a个子问题。如果分解问题成子问题需要时间D(n),合并子问题的解成原问题的解需要时间C(n),那么得到递归式:
T(n)=Θ(1)若n≤c
aT(n/b)+D(n)+C(n)其他
在第4章中,我们将看到如何求解这类常见的递归式。
34
~
35
归并排序算法的分析
虽然MERGE-SORT的伪代码在元素的数量不是偶数时也能正确地工作,但是,如果假定原问题规模是2的幂,那么基于递归式的分析将被简化。这时每个分解步骤将产生规模刚好为n/2的两个子序列。在第4章,我们将看到这个假设不影响递归式解的增长量级。
下面我们分析建立归并排序n个数的最坏情况运行时间T(n)的递归式。归并排序一个元素需要常量时间。当有n>1个元素时,我们分解运行时间如下:
分解:分解步骤仅仅计算子数组的中间位置,需要常量时间,因此,D(n)=Θ(1)。
解决:我们递归地求解两个规模均为n/2的子问题,将贡献2T(n/2)的运行时间。
合并:我们已经注意到在一个具有n个元素的子数组上过程MERGE需要Θ(n)的时间,所以C(n)=Θ(n)。
当为了分析归并排序而把函数D(n)与C(n)相加时,我们是在把一个Θ(n)函数与另一个Θ(1)函数相加。相加的和是n的一个线性函数,即Θ(n)。把它与来自“解决”步骤的项2T(n/2)相加,将给出归并排序的最坏情况运行时间T(n)的递归式:
T(n)=Θ(1)若n=1
2T(n/2)+Θ(n)若n>1(2.1)
在第4章,我们将看到“主定理”,可以用该定理来证明T(n)为Θ(nlgn),其中lgn代表log2n。因为对数函数比任何线性函数增长要慢,所以对足够大的输入,在最坏情况下,运行时间为Θ(nlgn)的归并排序将优于运行时间为Θ(n2)的插入排序。
为了直观地理解递归式(2.1)的解为什么是T(n)=Θ(nlgn),我们并不需要主定理。把递归式(2.1)重写为:
T(n)=c若n=1
2T(n/2)+cn若n>1(2.2)
其中常量c代表求解规模为1的问题所需的时间以及在分解步骤与合并步骤处理每个数组元素所需的时间。
36
相同的常量一般不可能刚好既代表求解规模为1的问题的时间又代表在分解步骤与合并步骤处理每个数组元素的时间。通过假设c为这两个时间的较大者并认为我们的递归式将给出运行时间的一个上界,或者通过假设c为这两个时间的较小者并认为我们的递归式将给出运行时间的一个下界,我们可以回避这个问题。两个界的阶都是nlgn,合在一起将给出运行时间为Θ(nlgn)。
图2-5图示了如何求解递归式(2.2)。为方便起见,假设n刚好是2的幂。图的(a)部分图示了T(n),它在(b)部分被扩展成一棵描绘递归式的等价树。项cn是树根(在递归的顶层引起的代价),根的两棵子树是两个较小的递归式T(n/2)。(c)部分图示了通过扩展T(n/2)再推进一步的过程。在第二层递归中,两个子结点中每个引起的代价都是cn/2。我们通过将其分解成由递归式所确定的它的组成部分来继续扩展树中的每个结点,直到问题规模下降到1,每个子问题只要代价c。(d)部分图示了结果递归树。
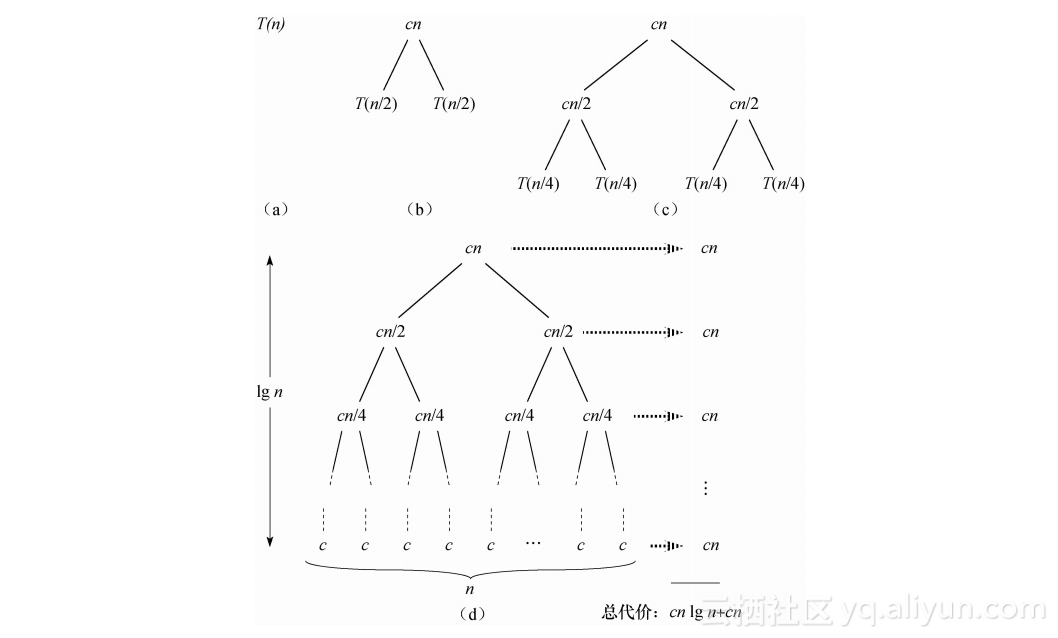
图2-5 对递归式T(n)=2T(n/2)+cn,如何构造一棵递归树。(a)部分图示T(n),它在(b)~(d)部分被逐步扩展以形成递归树。在(d)部分,完全扩展了的递归树具有lgn+1层(即如图所示,其高度为lgn),每层将贡献总代价cn。所以,总代价为cnlgn+cn,它就是Θ(nlgn)
接着,我们把穿过这棵树的每层的所有代价相加。顶层具有总代价cn,下一层具有总代价c(n/2)+c(n/2)=cn,下一层的下一层具有总代价c(n/4)+c(n/4)+c(n/4)+c(n/4)=cn,等等。一般来说,顶层之下的第i层具有2i个结点,每个结点贡献代价c(n/2i),因此,顶层之下的第i层具有总代价2ic(n/2i)=cn。底层具有n个结点,每个结点贡献代价c,该层的总代价为cn。
图2-5中递归树的总层数为lgn+1。其中n是叶数,对应于输入规模。一种非形式化的归纳论证将证明该断言。n=1时出现基本情况,这时树只有一层。因为lg1=0,所以有lgn+1给出了正确的层数。作为归纳假设,现在假设具有2i个叶的递归树的层数为lg2i+1=i+1(因为对i的任何值都有lg2i=i)。因为我们假设输入规模是2的幂,所以下一个要考虑的输入规模是2i+1。具有n=2i+1个叶的一棵树比具有2i个叶的一棵树要多一层,所以其总层数为(i+1)+1=lg2i+1+1。
为了计算递归式(2.2)表示的总代价,我们只要把各层的代价加起来。递归树具有lgn+1层,每层的代价均为cn,所以总代价为cn(lgn+1)=cnlgn+cn。忽略低阶项和常量c便给出了期望的结果Θ(nlgn)。
练习
2.3-1 使用图2-4作为模型,说明归并排序在数组A=〈3,41,52,26,38,57,9,49〉上的操作。
37
~
38
2.3-2 重写过程MERGE,使之不使用哨兵,而是一旦数组L或R的所有元素均被复制回A就立刻停止,然后把另一个数组的剩余部分复制回A。
2.3-3 使用数学归纳法证明:当n刚好是2的幂时,以下递归式的解是T(n)=nlgn。
T(n)=2若n=2
2T(n/2)+n若n=2k,k>1
2.3-4 我们可以把插入排序表示为如下的一个递归过程。为了排序A[1..n],我们递归地排序A[1..n-1],然后把A[n]插入已排序的数组A[1..n-1]。为插入排序的这个递归版本的最坏情况运行时间写一个递归式。
2.3-5 回顾查找问题(参见练习2.1-3),注意到,如果序列A已排好序,就可以将该序列的中点与v进行比较。根据比较的结果,原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程,每次都将序列剩余部分的规模减半。为二分查找写出迭代或递归的伪代码。证明:二分查找的最坏情况运行时间为Θ(lgn)。
2.3-6 注意到2.1节中的过程INSERTION-SORT的第5~7行的while循环采用一种线性查找来(反向)扫描已排好序的子数组A[1..j-1]。我们可以使用二分查找(参见练习2.3-5)来把插入排序的最坏情况总运行时间改进到Θ(nlgn)吗?
*2.3-7 描述一个运行时间为Θ(nlgn)的算法,给定n个整数的集合S和另一个整数x,该算法能确定S中是否存在两个其和刚好为x的元素。