《高阶Perl》——1.3　汉诺塔

1.3　汉诺塔

目前这两个例子都不是真需要递归的，它们都可以用简单的循环重写。

这类重写总是可能的，因为毕竟计算机的机器语言可能不支持递归，那么在某种程度上，它必然是非必需的。重写阶乘函数是简单的，但也不总是这样。这里有个例子。是1883年Edouard Lucas首次发表的难题，称为汉诺塔。

这个难题有三根桩，分别称为A、B和C。在A桩上是一个尺寸分等级的盘子叠成的塔，最大的在底部，最小的在顶部（见图1-1）。

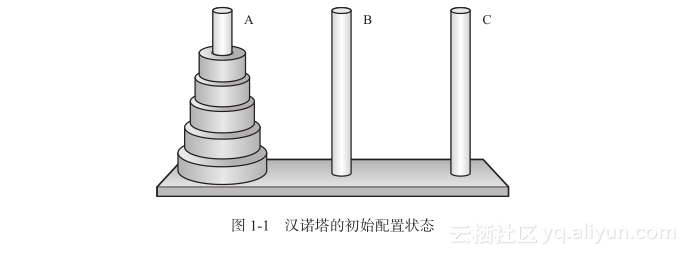
难题是要把整个塔从A桩移到C桩，并依照以下限制：一次只能移动一个盘子，且任何盘子都不能停留在比它小的盘子上面。盘子的数目由提出问题的人决定，但通常是64。尝试解决这个问题的一般形式：n个盘子。

考察n个盘子中最大的，它是在底部的盘子。这个盘子称为“最大的盘子”。最大的盘子开始时在A桩，最后希望它在C桩的最下面。如果有其他盘子在A桩，它们在最大盘子的上面，因此无法移动它。如果其他盘子都在C桩，将无法移动最大盘子到C桩，因为它会在一些较小盘子的上面。所以如果想把最大盘子从A桩移动到C桩，所有其他的盘子必须在B桩上按大小次序堆着，最小的在顶部（见图1-2）。

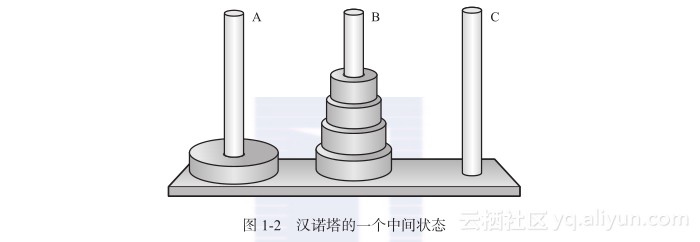
这意味着要解决这个问题，子目标是：必须把整个塔，除了最大的盘子，从A桩移动到B桩。只有这样才能把最大的盘子从A桩移动到C桩。在那以后，将可以把剩余的塔从B桩移动到C桩，这是另一个子目标。

幸运的是，当移动较小的塔时，可以忽略最大的盘子，不管它在哪里都不影响。这说明可以用相同的逻辑移动较小的塔：在较小的塔的底部是大盘子，把剩下的塔移走，再把这个底部的盘子移到正确的地方，然后再把剩下的较小的塔移到它的上面。但是怎样移动剩下的较小的塔呢？用同样的方法。

当需要移动的小塔仅有一个盘子，也就是此桩整个盘塔中最小的盘子时，过程就可以宣告结束了。在那种情况下的子目标很简单，只要把这个小盘子放到需要的地方。由于在它之上不会有其他盘子（因为会犯规），而且总是可以把它移动到任何想要的地方，它是最小的，因此不可能在其上放个更小的了。

移动最初的盘塔的策略如下。

要把n个盘子的盘塔从开始的桩子移动到最后的桩子：

1）如果“盘塔”实际上只有一个盘子，那就移动它。
2）否则用这个方法把除了盘子n（最大的盘子）之外所有的盘子从开始桩移动到辅助桩。
3）把盘子n（最大的盘子）从开始桩移动到最末桩。
4）用这个方法把辅助桩上的所有盘子移到最末桩。

很容易把它翻译成代码：

### Code Library: hanoi
# hanoi(N, start, end, extra)
# Solve Tower of Hanoi problem for a tower of N disks,
# of which the largest is disk #N. Move the entire tower from
# peg 'start' to peg 'end', using peg 'extra' as a work space
sub hanoi {
  my ($n, $start, $end, $extra) = @_;
  if ($n == 1) {
    print "Move disk #1 from $start to $end.\n";   # Step 1
  } else {
    hanoi($n-1, $start, $extra, $end);             # Step 2
    print "Move disk #$n from $start to $end.\n";  # Step 3
    hanoi($n-1, $extra, $end, $start);             # Step 4
  }
}

这个函数输出了一系列移动盘塔的指令。例如，要它指示移动一个由三个盘子组成的盘塔，可以这样调用它：

hanoi(3, 'A', 'C', 'B');

它的输出是：

    Move disk #1 from A to C.
    Move disk #2 from A to B.
    Move disk #1 from C to B.
    Move disk #3 from A to C.
    Move disk #1 from B to A.
    Move disk #2 from B to C.
    Move disk #1 from A to C.

如果想要一个移动盘子的图形化的输出替代简单的指示输出，可以把print语句替换成更有想象力的东西。但是可以参数化输出行为使软件更加灵活。hanoi()没有将print语句固定，而是接受一个额外的参数，即每次hanoi()想要移动盘子时将调用的函数。这个函数将输出一条指令，或刷新一个图形显示，或别的想要的任何东西。这个函数将传入盘子的号码、来源桩和目标桩。代码几乎完全一样：

sub hanoi {
  my ($n, $start, $end, $extra, $move_disk) = @_;
  if ($n == 1) {
    $move_disk->(1, $start, $end);
  } else {
    hanoi($n-1, $start, $extra, $end, $move_disk);
    $move_disk->($n, $start, $end);
    hanoi($n-1, $extra, $end, $start, $move_disk);
  }
}

要得到原始版本的行为，可以这样调用hanoi()：

sub print_instruction {
  my ($disk, $start, $end) = @_;
  print "Move disk #$disk from $start to $end.\n";
}

hanoi(3, 'A', 'C', 'B', \&print_instruction);

表达式&print_instruction生成一个代码引用（code reference），即一个表示该函数的标量。可以像别的标量一样在一个标量变量中保存代码引用，或者像别的标量一样作为一个参数传递，还可以使用这个引用执行它表示的函数。要那样做，可以写成：

$code_reference->(arguments...);

这将以指定的参数执行函数。代码引用通常称为coderef。

hanoi()的代码引用参数称为回调（callback），因为它是由hanoi()的主调者提供的函数，在hanoi()需要帮助时回调它。有时为hanoi()的参数$move_disk也称为吊钩（hook），因为它提供了一个地方以供额外的功能可以被容易地吊着。

现在有一个通用版本的hanoi()，可以通过传递一个保留盘子的移动轨迹的$move_disk函数测试算法，并确保没有违反任何规则：

### Code Library: check-move
@position = ('', ('A') * 3); # Disks are all initially on peg A

sub check_move {
  my $i;
  my ($disk, $start, $end) = @_;

check_move()函数维护一个数组，@position，它记录了所有盘子的当前位置。最初，所有盘子都在A桩。此处假设只有3个盘子，所以把$position[1]、$position[2]和$position[3]都设为"A"。$position[0]是个从来不用的虚设元素，因为没有盘子的编号是0。每次主函数hanoi()想要移动一个盘子，它就调用check_move()。

  if ($disk < 1 || $disk > $#position) {
    die "Bad disk number $disk. Should be 1..$#position.\n";
  }

这是个常规检查以确保hanoi()不会试图移动一个不存在的盘子。

  unless ($position[$disk] eq $start) {
    die "Tried to move disk $disk from $start, but it is on peg
                                       $position[$disk].\n";
  }

这里的函数检查确保hanoi()不会尝试从没有盘子的桩上移走盘子。如果起始桩与check_move()有关盘子当前位置的意见不一致，那么函数会产生一个错误信号。

  for $i (1 .. $disk-1) {
    if ($position[$i] eq $start) {
      die "Can't move disk $disk from $start because $i is on top of it.\n";
    } elsif ($position[$i] eq $end) {
      die "Can't move disk $disk to $end because $i is already there.\n";
    }
  }

这是真正有趣的检查。函数循环了比hanoi()试图要移动的盘子更小的所有盘子，以确认更小的盘子没有挡在（大盘子）要移动的路径上。第一个if分支确认每个更小的盘子不在hanoi()想要移动的盘子的上面，第二个分支确认hanoi()不会尝试把当前盘子移动到较小盘子的上面。

  print "Moving disk $disk from $start to $end.\n";
  $position[$disk] = $end;
}

最后，函数结束了，没有移错，因此和前面一样输出一条消息，并调整数组@position以反映盘子的新位置。

运行：

hanoi(3, 'A', 'C', 'B', \&check_move);

产生和前面一样的输出，没有错误，hanoi()没有违反任何规则。

这个例子证明了一个很重要的技术：通过把函数的部分功能参数化成调用其他函数，而不是固定其行为，可以使函数更灵活。这增加的灵活性会在想要函数做些改变时带来好处，例如，执行一次自动的自我检查。不是用许多可选的自测代码把函数弄乱，而是把测试部分与主算法分离。算法依旧保持简洁明了，而且能在运行时通过传递不同的代码引用参数使用或不使用自测代码。