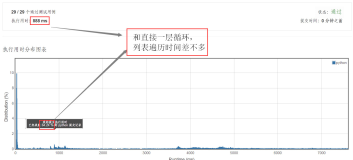
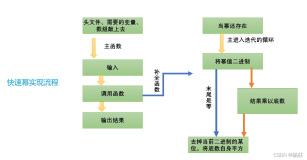
前几天做了一个关于欧拉函数的题,当时就做超时了,因为我是暴力做的,后来百度了一下 线性晒法求欧拉函数,所以今天就打算系统的看一下筛法求欧拉函数的问题,该算法在可在线性时间内筛素数的同时求出所有数的欧拉函数:
先介绍一下暴力的欧拉函数:
Eular(m) = m - (1-1/p1) - (1-1/p2) - ... - (1-1/pk) [其中 p1, p2...pk为m的素因子]
int Eular(int m)
{
int ret = m;
for(int i=2; i<m; i++)
{
if(m%i == 0)
ret -= ret/i;
while(m%i == 0)
{
m /= i;
}
}
if(m > 1)
ret -= ret/m;
return ret;
}
通过上述代码 我们发现它的复杂度还是挺高的~,所以在一些题目中可能不适合,会超时,所以我们就可以根据素数筛那样进行欧拉筛法:
要想求欧拉函数需要用到以下几个性质( p为素数 ):
1. phi(p) == p-1 因为素数p除了1以外的因子只有p,所以与 p 互素的个数是 p - 1个
2. phi(p^k) == p^k - p^(k-1) == (p-1) * p^(k-1)
证明:
令n == p^k,小于 n 的正整数共有 p^k-1 个,其中与 p 不互素的个数共 p^(k-1)-1 个,它们是 1*p,2*p,3*p ... (p^(k-1)-1)*p
所以phi(p^k) == (p^k-1) - (p^(k-1)-1) == p^k - p^(k-1) == (p-1) * p^(k-1)。
3. 如果i mod p == 0, 那么 phi(i * p) == p * phi(i) (证明略)
举个例子:
假设 p = 3,i = 6,p * i = 18 = 2 * 3^2;
phi(3 * 6) == 18*(1-1/2)*(1-1/3) = 6
p * phi(i) = 3 * phi(6) = 3 * 6 * (1-1/2) * (1-1/3) = 6 = phi(i * p) 正确
4. 如果i mod p != 0, 那么 phi(i * p) == phi(i) * (p-1)
证明:
i mod p 不为0且p为质数, 所以i与p互质, 那么根据积性函数的性质 phi(i * p) == phi(i) * phi(p) 其中phi(p) == p-1
所以 phi(i * p) == phi(i) * (p-1).
再举个例子:
假设i = 4, p = 3, i * p = 3 * 4 = 12
phi(12) = 12 * (1-1/2) * (1-1/3) = 4
phi(i) * (p-1) = phi(4) * (3-1) = 4 * (1-1/2) * 2 = 4 = phi(i * p)正确
了解了这些性质之后 我们要做的就是就是写程序了,具体咋写呢,就让我们参考一下素数筛,然后就可以写啦。
My Code:
#include <iostream>
#include <cstring>
using namespace std;
const int MAXN = 1e6+5;
bool flag[MAXN];///标记数组
int phi[MAXN];///欧拉函数值,i的欧拉函数值=phi[i]
int p[MAXN];///素因子的值
int cnt = 0;
void Get_phi()///筛法求欧拉函数
{
cnt = 0;
memset(flag, true, sizeof(flag));
phi[1] = 1;
for(int i=2; i<MAXN; i++)///线性筛法
{
if(flag[i])///素数
{
p[cnt++] = i;
phi[i] = i-1;///素数的欧拉函数值是素数 - 1
}
for(int j=0; j<cnt; j++)
{
if(i*p[j] > MAXN)
break;
flag[i*p[j]] = false;///素数的倍数,所以i*p[j]不是素数
if(i%p[j] == 0)///性质:i mod p == 0, 那么 phi(i * p) == p * phi(i)
{
phi[i*p[j]] = p[j] * phi[i];
break;
}
else
phi[i*p[j]] = (p[j]-1) * phi[i];///i mod p != 0, 那么 phi(i * p) == phi(i) * (p-1)
}
}
}
int main()
{
Get_phi();
int m;
while(cin>>m)///测试
{
cout<<phi[m]<<endl;
}
return 0;
}
练习题: