本节书摘来自华章出版社《数值分析(原书第2版)》一 书中的第1章,第1.3节,作者:(美)Timothy Sauer,更多章节内容可以访问云栖社区“华章计算机”公众号查看。
1.3 精度的极限
数值分析的一个目标是在给定的精度级别中估计结果.使用双精度意味着我们使用52位精度(大约16位十进制数字)来保存和操作数字.
得到的答案里总能有16位正确的有效数字吗?在第0章中已经表明,计算二次方程的朴素算法可能丢失部分或者所有的有效数字.一个改进的算法可以消除这种问题.在本节中,我们可以看到一些新的计算问题,利用双精度计算机不能得到16位正确的有效数字,即便使用最好的算法.43
1.3.1 前向与后向误差
第一个例子表明在某种情况下,铅笔和纸做得比计算机还好.
例1.7 使用二分法计算函数f(x)=x3-2x2+43x-827的根,精确到小数点后6位.
注意到f(0)f(1)=(-8/27)(1/27)<0,所以中值定理保证在区间[0,1]中存在一个根.根据例1.2,使用二分法20步就可以具有6位精度.
事实上,不使用计算机,很容易验证r=2/3=0.666666666…是一个根:f(2/3)=827-249+4323-827=0二分法可以得到多少位?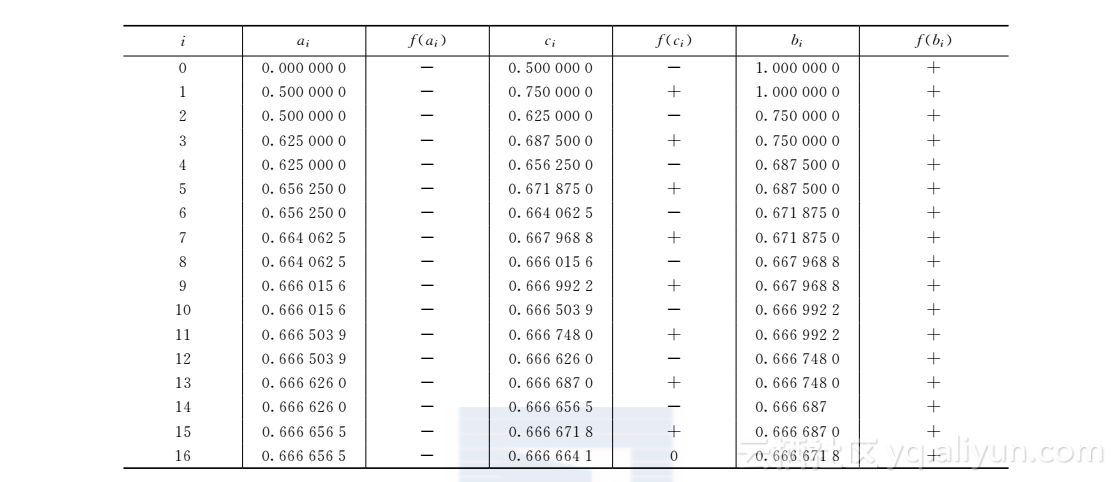
令人惊讶的是,二分法在16步计算后停止了,其中f(0.6666641)=0.如果我们关注6位或者更多位的精度,这是一个严重的错误.图1.7显示了问题的困难之处.只要只用IEEE双精度标准,就有很多在根r=2/3的10-5范围以内的浮点数字对应的函数值为机器0,因而它们有同等的权利被称为根!而且问题可能变得更糟,尽管函数f单调增加,图1.7b甚至表明函数f的双精度值的符号常常是错的.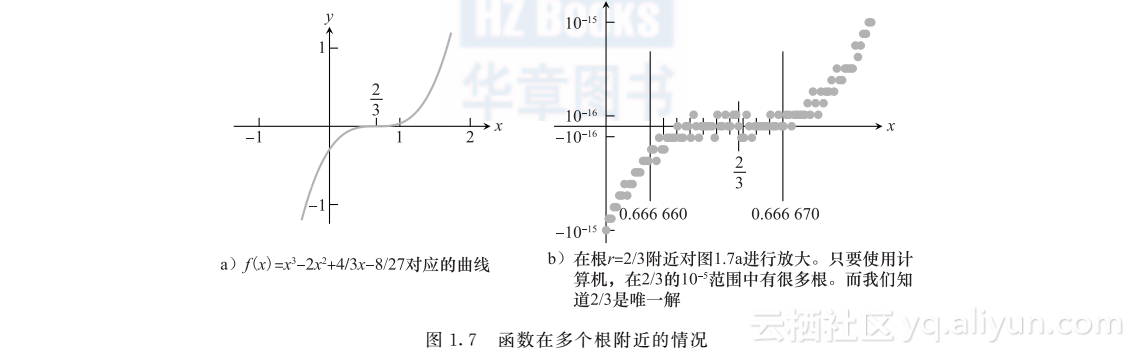
图1.7表明问题不仅出在二分法里,而且出在双精度算术无法在根附近足够精确地计算函数f.任何其他依赖这种计算机算术的方法都可能失败.对于这个例子,16位精度甚至不能检查6位精度的候选解是否正确.
为了说服大家这不是二分法的问题,我们使用MATLAB的最高性能的多用途根求解器,fzero.m.我们在本章的后面来讨论细节.
现在,我们仅仅需要把函数和初始估计输入函数.它也没有更幸运:
在这个例子中,所有方法都没能找到5位以上的正确数位的原因从图1.7中看得很清楚.以双精度进行计算时,任何方法中已知的信息就是函数.如果计算机算术中函数在一个非根的地方的值为0,则没有什么方法可以修复这个问题.另一种陈述这个难点的方式为:在y轴上近似解可以足够接近真实解,但是它们在x轴上并不接近.
这些观察激发了一些重要的定义.
定义1.8 假设f是一个函数,r是一个根,意味着满足f(r)=0.假设xa是r的近似值.对于根求解问题,近似xa的后向误差是f(xa),前向误差是r-xa.
“后向”和“前向”的使用可能需要一些解释.我们的观点认为寻找根的过程在中间.问题是输入,解是输出:定义问题的数据→求解过程→解在本章中,“问题”是单变量的方程,“求解过程”是求解方程的44
~
45算法:方程→方程求解器→解后向误差在左边或者输入一侧(问题数据).这是我们需要对于问题(函数f)改变的量使得方程平衡并输出近似解xa.这个量是f(xa).前向误差是右边或者输出一侧(问题求解).这是我们对于近似解要做的修正,该误差是r-xa.
例1.7的难点是,根据图1.7,后向误差接近εmach≈2.2×10-16,而前向误差大约为10-5.双精度数不能在机器精度的相对误差以下可靠计算,因为后向误差不能被可靠降低,同时前向误差也不能减小.
例1.7是一个非常特殊的例子,函数f在r=2/3具有三阶根.注意到f(x)=x3-2x2+43x-827=x-233这是一个关于多根的例子.
定义1.9 假设r是可微函数f的根;也就是说,假设f(r)=0.则如果0=f(r)=f′(r)=f″(r)=…=f(m-1)(r),但是f(m)(r)≠0,我们说函数f在r点具有m重根.当多重性大于1,我们说函数f在r点具有重根.当多重性等于1时,根被称为单根.
例如,由于f(0)=0,f′(0)=2(0)=0,但是f″(0)=2≠0,所以f(x)=x2在r=0处具有二重根,或者双根.类似地,f(x)=x3在r=0处具有三重根,而f(x)=xm则具有m重根.例1.7在r=2/3处具有三重根.
由于函数在多根附近十分平缓,前向和后向误差之间在近似解的附近存在很大的不一致.后向误差在垂直方向进行度量,通常比在水平方向度量的前向误差要小得多.
例1.8 函数f(x)=sinx-x在r=0处有三重根.找出近似根在xc=0.001处的前向和后向误差.
零是函数的三重根,原因如下:f(0)=sin0-0=0
f′(0)=cos0-1=0
f″(0)=-sin0-0=0
f(0)=-cos0=-1前向误差FE=r-xa=10-3.后向误差是一个常数,需要加到f(x)上,使xa成为一个根,即BE=f(xa)=sin(0.001)-0.001≈1.6667×10-10.
前向和后向误差的讨论与方程求解器的终止条件有关.目的是找到根r满足f(r)=0.假设我们的算法可以生成一个近似解xa.我们如何确定这个解有多好?
我们想到两种可能:1)使得xa-r足够小,2)使得f(xa)足够小.当xa=r时,由于两种方式看起来都一样,所以做不出决定.但是我们很少会如此幸运地遇到这种情况.在更加典型的情况下,方法1)和2)不同,并分别对应前向和后向误差.
究竟前向误差还是后向误差更合适,这依赖于问题所处的环境.如果我们使用二分法,两种误差都可观测到.对于近似根xa,我们通过对f(xa)计算可以得到后向误差,46前向误差不会大于当前区间一半的长度.对于FPI,由于我们没有括住的区间,选择会更加有限.和前面一样,后向误差通过f(xa)可以知道,但是如果想知道前向误差,则需要知道真实解,而解正是我们试图要计算的未知项.
方程求解方法的终止条件可以基于前向或者后向误差.还有其他相关的终止条件,诸如计算时间的上限.问题的上下文对于我们的选择具有指导作用.
由于函数在多重根位置上f′为0,所以在重根附近形状很平.正因为如此,分离重根可能会遇到困难,这也正如我们已经证实的情况.但是多重根问题仅仅是冰山一角.没有多重根问题时也可能也会出现问题,正如下一节将要讲述的问题.
1.3.2 威尔金森多项式
一个难以进行数值求解的单根例子在威尔金森[1994]的论著中进行了讨论.威尔金森多项式是W(x)=(x-1)(x-2)…(x-20)(1.19)当把所有乘法展开,如下:W(x)=x20-210x19+20615x18-1256850x17+53327946x16-1672280820x15
+40171771630x14-756111184500x13+11310276995381x12
-135585182899530x11+1307535010540395x10-10142299865511450x9
+63030812099294896x8-311333643161390640x7
+1206647803780373360x6-3599979517947607200x5
+8037811822645051776x4-12870931245150988800x3
+13803759753640704000x2-8752948036761600000x
+2432902008176640000(1.20)根是1~20之间的整数.但是,当W(x)根据(1.20)中它的未分解形式进行定义,它的求值计算会由于近似相等、大数字的消去而有损失.为了观察这对于根求解带来的影响,通过输入(1.20)的非分解形式,或者从本书网站上获取,定义MATLAB的m文件wilkpoly.m.
我们仍然使用MATLAB的fzero.为了使之尽可能简单,我们将一个真实解x=16输入作为一个初始估计出:
令人惊讶的是,MATLAB不能返回第二个正确的小数位,即使对于一个单根r=16.这是由于算法自身的缺陷,包括fzero和二分法都有相似的问题,这与不动点迭代和任何其他的浮点方法相似.参考威尔金森工作中关于多项式这一部分,他在1984年写道:“对我个人而论,我把这看做在我的数值分析生涯里最惨痛的经历.”W(x)的根很干净:整数x=1,…,20.威尔金森惊讶于求解根过程中保存系数时很小的误差会对结果产生很大的影响,这个问题我们刚刚在前面的讨论中看到过.47
如果使用(1.19)分解形式计算威尔金森多项式,求解精确根的问题就消失了.当然,如果多项式在我们开始之前就分解好了,也就没有求根计算的必要了.
1.3.3 根搜索的敏感性
威尔金森多项式和例1.7中的三重根问题,由于相同的原因造成求解的困难——方程中小的求解误差造成求解根中的大误差.如果在输入中是一个小误差,在这种情况下对问题进行求解,造成输出中的大问题,这样的问题被称为敏感性问题.在本节中我们将量化误差,并引入误差放大因子和条件数概念.
为了理解究竟是什么造成了误差的放大,我们将建立公式以理解当方程改变时,根能移动多远.假设问题是找到f(x)=0的根r,但是对输入做了一个小变化εg(x),其中ε很小.令Δr是对应根中的变化,因而f(r+Δr)+εg(r+Δr)=0将f和g展开为一阶泰勒多项式f(r)+(Δr)f′(r)+εg(r)+ε(Δr)g′(r)+O((Δr)2)=0其中我们使用“大O”标识O((Δr)2)代表包含(Δr)2项和Δr的更高阶项.对于小的Δr,O((Δr)2)可以忽略,并得到(Δr)(f′(r)+εg′(r))≈-f(r)-εg(r)=-εg(r)或者Δr≈-εg(r)f′(r)+εg′(r)≈-εg(r)f′(r)假设和f′(r)相比,ε很小,并且f′(r)≠0.
(1.21)
例1.9 估计P(x)=(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)-10-6x7的最大根.
令f(x)=(x-1)(x-2)(x-3)(x-4)(x-5)(x-6),ε=-10-6,g(x)=x7.如果没有εg(x)项,最大根是r=6.问题是当我们加上这一项后,根发生了多少变化?
从敏感公式得到Δr≈-ε675!=-2332.8ε意味着在函数f(x)中相对大小ε的输入误差,在根中被一个超过2000的因子放大.我们估计P(x)的最大根是r+Δr=6-2332.8ε=6.0023328.对P(x)使用fzero我们得到正确的解6.0023268.48
例1.9中的估计足以告诉我们在根拟合的过程中误差如何放大.问题数据的第6位带来的误差给结果的第三位造成影响,意味着以误差放大因子2332.8,将会造成丢失三位有效数字.给这个因子一个名字将有所帮助.对于一个一般算法生成的近似xc.我们定义它的误差放大因子=相对前向误差相对后向误差前向误差指的是解的变化,该变化可以使得xa准确,在根求解问题中前向误差对应xa-r,后向误差指的是输入中的变化,该变化使得xc是正确的解.对于前向误差和后向误差有大量可以选择的方式,这依赖于我们想探索哪一种敏感性.用f(xa)改变常数项是一种选择,并在这一节的前面使用过,在敏感公式(1.21)对应于g(x)=1项.更一般地,任何输入数据的变化都可以用于后向误差,诸如在例1.9中选择g(x)=x7.在求解根过程中的误差放大因子如下误差放大因子=Δr/rεg(r)/g(r)=-εg(r)/(rf′(r))ε=g(r)rf′(r)(1.22)其中在例1.9中为67/(5!6)=388.8.
例1.10 用根的敏感公式,研究在威尔金森多项式中,x15项中的变化对于根r=16的影响.并对这个问题找出误差放大因子.
定义扰动函数Wε(x)=W(x)+εg(x),其中g(x)=-1672280820x15,注意到W′(16)=15!4!(参见习题7).利用式(1.21),根中的变化可以近似为Δr≈16151672280820ε15!4!≈6.1432×1013ε(1.23)就现实情况来讲,从第0章我们知道,对于每个保存的数字都有和机器精度同样阶的相对误差.在x15项中的变化εmach将使得根r=16相对移动Δr≈(6.1432×1013)(±2.22×10-16)≈±0.0136其对应根是r+Δr≈16.0136,和1.3.2节中的差异并不大.当然,在威尔金森多项式中其他关于x的幂对于误差的形成也有贡献,所以真实的情况会变得非常复杂.但是敏感性公式使得我们可以看到大量误差放大背后的机制.
最后,从式(1.22)可以计算误差放大因子g(r)rf′(r)=1615167228082015!4!16≈3.8×1012误差放大因子的重要性在于,它告诉我们16位数位的操作精度在输入和输出的过程中会有多少位丢失.对于误差放大因子是1012的问题,我们期望在计算过程中会丢掉16位中的12位有效数字,从而在根中仅仅留下了4个有效数字,这就是威尔金森近似xc=16.014…所面临的问题.49 条件 这是条件数第一次出现,条件数也是误差放大度量的一种方式.数值分析是对算法的研究,算法把定义问题的数据作为输入,对应的结果作为输出.条件数指的是理论问题本身所带来的误差放大部分,和用于求解问题的特定算法无关.
注意到条件数仅仅度量由于问题本身带来的误差放大,这点很重要.和条件一起,还有一个平行概念,即稳定,稳定指的是由于算法小的输入误差造成的放大,而不是问题本身.如果一个算法在小的后向误差存在的时候,总能给出一个近似解,则称该算法是稳定的.如果问题的条件好,算法稳定,我们可以期望同时具有小的后向误差和前向误差.
前面的误差放大例子表明根求解过程对于特定的输入变化的敏感性.问题可能或多或少地敏感,依赖于如何设计输入的变化.问题的条件数定义为所有输入变化,或者至少规定类型的变化所造成的最大误差放大.条件数高的问题称为病态问题,条件数在1附近的问题称为良态问题.在第2章中讨论矩阵问题时,我们将返回这个问题.
1.3节习题
1.找出下列函数的前向和后向误差,其中根3/4的近似根是xa=0.74:
(a) f(x)=4x-3(b) f(x)=(4x-3)2
(c) f(x)=(4x-3)3(d) f(x)=(4x-3)1/3
2.找出下列函数的前向和后向误差,其中根1/3的近似根是xa=0.3333:
(a) f(x)=3x-1(b) f(x)=(3x-1)2
(c) f(x)=(3x-1)3(d) f(x)=(3x-1)1/3
- (a) 找出函数f(x)=1-cosx在根r=0处的多重性.(b)找出前向和后向误差,近似根是xa=0.0001.
4.(a) 找出函数f(x)=x2sinx2在r=0处的重根.(b) 找出前向和后向误差,近似根是xa=0.01.
5.找出前向和后向误差之间的关系,并确定线性函数f(x)=ax-b的根.
6.令n是一个正整数.定义正数A的n阶根是xn-A=0.(a) 确定这是几重根.(b) 证明对于具有较小前向误差的近似的n阶根,后向误差可近似表示为前向误差的nA(n-1)/n倍.
7.令W(x)是威尔金森多项式.(a) 证明W′(16)=15!4!.(b) 找到W′(j)的类似公式,其中j是1~20之间的一个整数.
8.令f(x)=xn-axn-1,并设置g(x)=xn.(a) 使用敏感性公式预测函数fε(x)=xn-axn-1+εxn的非0根,其中ε很小.(b) 找出非0根,并同预测值进行对比.50
1.3节编程问题
1.令f(x)=sinx-x.(a) 寻找r=0对应的重根.(b)使用MATLAB的fzero命令,初始估计x=0.1,并确定根.fzero报告的前向和后向误差是多少?
2.对于函数f(x)=sinx3-x3,进行问题1中的计算.
3.(a) 使用fzero找到函数f(x)=2xcosx-2x+sinx3在区间[-0.1,0.2]中的根.报告前向和后向误差.(b)以初始区间[-0.1,0.2]运行二分法.找到尽可能多的正确数位,并报告结论.
4.(a) 使用式(1.21)近似函数fε(x)=(1+ε)x3-3x2+x-3在3附近的根,ε是常数.(b) 令ε=10-3,找出实际的根,并与(a)部分的结果进行比较.
5.使用式(1.21)近似函数f(x)=(x-1)(x-2)(x-3)(x-4)-10-6x6在r=4附近的根.找到误差放大因子.使用fzero检查该近似.
6.使用MATLAB命令fzero找出威尔金森多项式在x=15附近的根,x15系数的相对变化是ε=2×10-15,这使得系数变得更小一点.和式(1.21)中精度进行比较.