本节书摘来自华章计算机《算法基础》一书中的第2章,第2.3节,作者:(美)罗德·斯蒂芬斯(Rod Stephens)著,更多章节内容可以访问云栖社区“华章计算机”公众号查看
2.3 求幂运算
有时程序需要计算某数的正整数次幂,这在该幂指数不大时容易完成。例如,73可以通过计算7×7×7很容易地得到结果343。对于较大的幂,例如7102×187×291,这种计算过程是十分缓慢的。
注 计算较大的幂如7102×187×291可能很缓慢。但如果不是这种求幂运算在某些重要密码学中得到应用,人们也许不会十分关心它。
幸运的是,有一种较快的方法来执行这种运算。这种方法基于乘方运算的两个关键法则: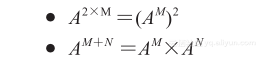
当这个幂是二次幂时,第一个法则可以迅速地计算出A的幂。
第二个法则能将这些A的幂结合以产生想要的结果。
以下伪代码展示了这个算法:
例如要计算出76。首先算法计算出71、72、74。由于下一个指数8比所需的6大,因此算法停止。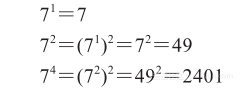
接下来算法使用第二个法则来从已经产生的二次幂中生成76。如果将6看作2的幂的和,6=2+4。使用第二个法则,得到76=72×74=49×2 401=117 649。
执行这个运算进行两次乘法来计算72和74再加上一次乘法来获得最终结果,即总共进行三次乘法运算。这比简单计算7×7×7×7×7×7进行了更少的乘法运算,但在本例中这只是一个小小的不同。
更普遍地,对于指数P,算法进行log(P)次运算来得到A的P次幂。然后算法检验A的二进制位数来确定它应当将其中的哪些乘在一起以获得最终结果。(如果P的二进制位数是1,那么最终的结果应当包含2的相应幂。在前例中,6的二进制表示是110,因此需要计算2的二次幂和四次幂,即22和24。)
在二进制中,数值P有log2(P)位,因此总共的运行时间复杂度是O(log P)+O(log P)=O(log P)。即使P为一百万,log(P)大约只有20,因此这个算法需运行20步左右(至多40次乘法)。这比一百万要小得多。
这种算法的一个限制是当指数很大时,幂增长得过快。即使一个如7300这样“小”的值也有254个十进制位。这意味着用来计算大指数幂庞大数相乘的过程是缓慢的,并且需要大量计算空间。
幸运的是,这种庞大的幂运算的最常见应用是加密算法,这种算法的运算限制在某个模中。尽管这个模通常较大,但仍能限制住运算数和结果的大小。例如如果某模有100位,两个100位数的积就不会大于200位。那么,接下来可以再次用这个模来得到一个不大于100位的结果。虽然用模将每一个数减小使得每步运算稍微变慢,但也意味着可以计算几乎无限大的值。