本节书摘来自华章计算机《算法基础》一书中的第1章,第1.4节,作者:(美)罗德·斯蒂芬斯(Rod Stephens)著,更多章节内容可以访问云栖社区“华章计算机”公众号查看
1.4 算法的特点
一个好的算法必须具备三个特点:正确性,可维护性和效率。
显然,如果一个算法不能解决问题,它就没什么用;如果它不能产生正确的答案,它就没有什么意义。
注 有趣的是,一些算法只在某些时候产生正确的答案,但是它们仍然有用。例如,某个算法或许能给你一些有用的信息。这种情况下,你可以重复运行这个算法很多次,来让你确信某个答案是正确的。在2.4.3节中描述的费马素性测试(Fermat抯 primality test)就是这种算法。
如果一个算法难以维护,在程序中使用它就是危险的。如果一个算法简单、直观、优雅,那么你可以确信它能够产生正确的结果;而且,当这个算法没有产生正确的结果时,你可以修正它。如果算法是复杂、混乱和令人费解的,那么实现它的时候可能会遇到很多麻烦。如果出现了错误,将费更多的时间和精力来修正它。如果一个算法很难理解,如何知道它是否产生了正确的结果呢?
注 这并不意味着研究令人困惑的复杂算法没有意义。即使你难以实现某个算法,也可能在尝试中学到很多东西。随着时间的推移,你在算法方面的直觉和技巧会渐渐增加,所以曾经认为是令人困惑的算法就显得更容易了。不过,必须始终全面地测试所有的算法以确保它们产生正确的结果。
大多数开发人员在提高效率上花费了大量精力。效率肯定是重要的。如果一个算法产生的结果正确并且易于实现和调试,但是用了7年时间来完成任务或者需要的内存比一个计算机可以容纳的还多,它仍然没有什么用。
为了研究一个算法的性能,计算机科学家探求算法的性能如何随着问题规模的改变而改变。如果你加倍了算法正在处理的数值,运行时间会加倍吗?运行时间会增加到原来的4倍吗?还是它突然成指数倍地增加以至于算法要花数年时间来完成?
你同样可以思考关于内存使用的问题或者关于算法需要的其他资源的问题。如果你加倍了问题的规模,需要的内存加倍了吗?
你还可以探索关于算法在不同情况下的性能问题。算法在最坏情况下性能如何?最坏情况有多大可能发生?如果你在许多随机数据中运行算法,它的平均性能如何?
为了刻画问题规模与性能的关系,计算机科学家使用下一节描述的大O符号。
1.4.1 大O符号
大O符号使用函数来描述数据规模增长到很大时算法的最坏性能是如何与问题规模相关的(这有时称为程序的渐近性能)。这个函数写在大写字母O后面的括号里。
例如,O(N2)是一个算法的运行时间(或者内存使用,抑或任何你想衡量的东西)的增长与输入N的平方成正比。如果加倍了输入的数据,运行时间大约增加到原来的4倍。如果把输入数据变为原来的3倍,运行时间增加到9倍。
注 通常O(N2)读作“order N squared”(N的平方)。例如,有人可能会说:“6.2.2节中的快速排序算法的最坏复杂度是N2。”
计算算法的大O符号有5个基本规则:
1)如果一个算法对于一个数学函数f执行一系列的步骤f(N)次,它需要O(f(N))步。
2)如果一个算法对于函数f执行了一个需要O(f(N))步的操作,然后对于函数g执行了第二个需要O(g(N))步的操作,这个算法的总体复杂度是O(f(N)+g(N))。
3)如果一个算法的复杂度是O(f(N)+g(N)),并且对于足够大的N,函数f(N)远大于g(N),这个算法的性能可以被简化为O(f(N))。
4)如果一个算法执行了一个需要O(f(N))步的操作,对于操作中的每一步执行了另外O(g(N))步,这个算法的总体复杂度是O(f(N)×g(N))。
5)忽略常数的倍数。如果C是一个常数,O(C×f(N))等同于O(f(N))。并且O(f(C×N))等同于O(f(N))。
仅使用f(N)和g(N)来描述这些规则可能会显得有些难以理解,但是应用它们相当容易。如果它们看起来令人困惑,看一些例子应该更容易理解它们。
1.规则1
如果一个算法对于一个数学函数f执行一系列的步骤f(N)次,它需要O(f(N))步。
思考下列用伪代码写的搜索数组中最大整数的算法:
这个FindLargest(寻找最大值)算法需要一个整数数组作为参数并返回一个整数结果。
这个算法开始把变量largest设为数组中的第一个值,然后循环数组中的剩余值,把每一个值与largest比较。如果找到的一个值比largest还大,这个程序就让largest等于那个值。
在完成循环后,这个算法返回largest。
这个算法对于数组中的N个元素的每一个都检查了一次,所以说它的复杂度是O(N)。
注 通常一个算法把大多数时间花费在循环上。如果一个算法没有包含循环,它就不能在有限的代码中执行超过N步的操作。
研究一个算法的循环来分析清楚它花费了多少时间。
2.规则2
如果一个算法对于函数f执行了一个需要O(f(N))步的操作,然后对于函数g执行了第二个需要O(f(N))步的操作,这个算法的总体复杂度是O(f(N)+g(N))。
如果再看一次前面的FindLargest算法,就会发现有些步骤并不在循环里。下面的伪代码展示了相同的步骤,并且它们的时间复杂度显示在右边的注释中。
这个算法在进入循环之前执行了一步,在循环之后又执行了另一步。这两步都有O(1)的时间复杂度(它们都只是简单的一步),所以这个算法真正的总运行时间是O(1+N+1)。也可以用普通代数把它写作O(2+N)。
3.规则3
如果一个算法的复杂度是O(f(N)+g(N)),并且对于足够大的N,函数f(N)远大于g(N),这个算法的性能可以被简化为O(f(N))。
之前的例子FindLargest的时间复杂度是O(2+N)。当N增大时,函数N大于常量2,所以O(2+N)简化为O(N)。
当问题规模变得非常大时,忽略这些更小的函数可以让设计者专注于算法的渐近表现,也忽略相对较小的初始化和清除任务。如果一个算法花费一些时间建立简单的数据结构并准备进行大规模计算,只要这个建立结构的时间与主要计算时长比起来很小,就可以忽略这个时间。
4.规则4
如果一个算法执行了一个需要O(f(N))步的操作,对于操作中的每一步执行了另外O(g(N))步,这个算法的总体复杂度是O(f(N)×g(N))。
请思考下列判断数组中是否有重复项的算法。(注:这并不是判断数组中是否有重复项的最有效算法。)

这个算法包含了两个嵌套的循环。外层的循环遍历了数组中所有的N个元素,所以它花了O(N)步。
每次通过外层循环,里层的循环也遍历了数组中所有的N个元素,所以它也花了O(N)步。
因为一个循环嵌套在另一个中,组合的复杂度是O(N×N)=O(N2)。
5.规则5
忽略常数的倍数。如果C是一个常数,O(C×f(N))等同于O(f(N)),并且O(f(C×N))等同于O(f(N))。
如果再回看前面的ContainsDuplicates算法,会看到内层循环实际执行1~2步。它执行了一个If语句来检测i与j是否相同。如果它们不同,算法就比较array[i]和array[j]。算法也可能返回True。
如果忽略Return语句这一额外步骤(它至多执行一次),并且假定算法执行了所有的If语句(因为它大多数时候都被执行),内层循环需要O(2×N)步。因此,这个算法的总复杂度是O(N×2×N)=O(2×N2)。
由规则5知可忽略倍数2,所以这个算法的时间复杂度是O(N2)。这条规则真正回到了大O符号的目的,即感受随N增加时算法的表现。在这个例子中,假设N增加到2倍,如果把2×N代入到方程2×N2,会得到下列的式子:
2×(2×N)2=2×4×N2=8×N2
这是原始值2×N2的4倍,所以运行时间增加到4倍。
现在用由规则5简化的复杂度O(N2)来尝试同样的事情。把2×N带入到等式中,得到下列式子:
(2×N)2=4×N2
这是初始值N2的4倍。所以这也意味着运行时间增加到4倍。
无论使用公式2×N2还是N2,结果都是一样的:问题规模增加到2倍使运行时间增加到4倍。在这里,重要的不是常量,而是运行时间的增加与输入值N的平方成正比。
注大O符号只是为了让你了解算法的理论性能,记住这个是很重要的。实际操作中的结果可能不同。例如,假设一个算法的复杂度是O(N),而没有忽略常量时的实际执行的步数可能是100 000 000+N。这种情况下,除非N真的很大,否则你可能无法安全地忽略这个常量。
1.4.2 常见的运行时间函数
当研究算法的运行时间时,一些函数经常出现。下面列出了一些常见的运行时间函数。它们也给出一些观点,便于你了解一个复杂度为O(N3)的算法是否合理。
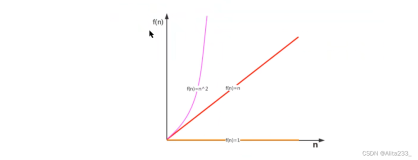
1.复杂度为O(1)的算法
复杂度为1的算法使用常数的时间,无论问题规模多么大。这种算法往往执行相对琐碎的任务,因为它们在O(1)时间里甚至都不能遍历输入内容。
例如,在某一刻快速排序需要选择数组中的一个值。理想的情况是,这个数应该是数组中间的数值,但是没有简单的方法判断哪一个数恰好在中间。(例如,如果数字均匀分布在1和100之间,50将是一个很好的分割数。)下列的算法展示了解决这个问题的一个常用方法:
这个算法选择了数组中开头、结束和中间的数值,比较它们,然后返回了这三个数的中间数值。这可能不是挑选整个数组中最佳元素的方法,但是这样做可以保证这并不是一个太糟糕的选择。
因为这个算法只执行了几步,它的复杂度是O(1)并且它的运行时间与输入N相互独立。(当然,这个算法并不是真正地独立,它只是一个更加复杂算法的一小部分。)
- 复杂度为O(log N)的算法
复杂度为O(log N)的算法通常在每一步中把它必须考虑的元素的数量除以一个固定的因数。
对数
底数a的某次幂是一个数b,这个幂就是b以a为底的对数。例如,log2(8)=3是因为23=8。这里,2是底。算法复杂度描述中通常以2为底,因为输入被连续地分成两组。正如很快就会看到的,对数项在大O符号中并不是真正重要的,因此它通常被省略。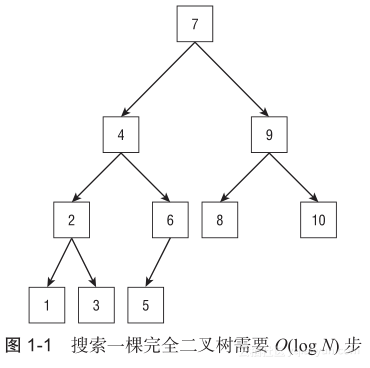
例如,图1-1展示了一棵完全排序二叉树。它是二叉树,因为每一个结点最多有两个分支。它是一棵完全树,因为每一层(可能除了最后一层)都是完全满的而且最后一层的节点都被放在左边。它是一棵排序树,故每一个结点的值的大小都在左右子节点的值之间。
下面的伪代码展示了一个在图1-1中的树中搜索特定元素的方法:


第10章将会详细介绍树算法,但是应该能从下列的讨论中了解这个算法的本质。
这个算法声明并初始化了变量test_node,这样它就指向了在顶端的树根的值。(传统上,计算机程序里的树是把根结点画在顶端的,并不像真实的树。)算法之后进入了一个循环。
如果tset_node是null(空),那么目标值就不在这棵树中,所以这个算法返回了null。
注 null是一个可以分配给变量的特殊值。这个变量应该指向一个对象,比如树中的的一个结点。null意味着“这个变量不指向任何东西。”
如果test_node就是目标值,其就是我们所寻找的结点。所以这个算法就返回了test_node。
如果我们搜索的target_value比test_node的值小,这个算法就让test_node等于其左孩子。(如果test_node位于树的底部,其LeftChild的值是null,算法会在下一个循环中解决这个问题。)
如果test_node的值不等于target_node并且不小于target_node,那它一定比target_node大。在那种情况下,这个算法使test_node的值等于它的右孩子。(同样的,如果test_node在树的底端,它的右孩子的值是null,算法会在下一个循环中解决这个问题。)
变量test_node沿着树向下移动,最后要么找到了目标值,要么在test_node是null时脱离树。
理解这个算法的复杂度是一个问题:在算法找到target_node或者脱离树之前,test_node必须要移动多远?
有时算法十分幸运,马上找到了目标值。如果在图1-1中目标值是7,这个算法只用一步就找到了它并停止。即使目标值不在根结点,例如,目标值是4时,这个程序在停止之前也只要检查这棵树的一小部分。
然而,在最坏的情况下,这个算法需要从树的顶端搜索到底端。
事实上,大约一半树的结点都是底端的结点,并且这些结点会有缺失孩子(目标结点)。如果一棵树是一棵满的完全二叉树,每一个结点都恰好有2或0个子结点,最底层将恰好有全部结点的一半。这意味着如果搜索一个在树中随机选取的值,这个算法在大多数情况下必须遍历这棵树的绝大多数层。
现在问题来了:这棵树有多高?一棵高为H的完全二叉树如果叶子全满,其有2H-1个结点。从另一个角度看,一棵包含N个结点满的完全二叉树的高度大约是log2(N)。因为在最坏(或平均)的情况下,这个算法从树的顶端搜索到底端,并且这棵树的高度大约是log2(N),所以这个算法的时间复杂度是log2(N)。
这时候对数一个有趣的特点发挥了作用。可以用下面的公式把一个以A为底的对数的底换为B。
logB(x)=logA(x)/logA(B)
设B=2,可以用这个公式把任何以A为底的对数转换成log2(N)的形式:
O(log2(N))=O(logA(N) / logA(2))
对于任何一个给定的A,1/logA(2) 是一个常量,并且大O符号忽略常量的倍数,所以,对于任何的底A,O(log2(N))都等同于O(logA(N)) 。因此,在底没有标明的时候,时间复杂度经常写作O(logN)(没有括号使其看起来更简洁)。
这个算法是一个典型的时间复杂度为O(log N)的算法。每一步算法都把它必须考虑的元素数目除以2。
因为在大O符号中log的底并不重要,这个算法用哪一个数来除元素没有关系。本例中每次把元素的数目除以2,这在很多对数算法中都很常见。如果算法把剩余元素的数目变为原来的十分之一,每次都取得很大进展,即使这样它的复杂度仍然是O(log N)。如果算法每次把元素的数目变为原来的9/10,进展不大,它的复杂度还是如此。
当N增长时,对数函数log(N)增长得相对较慢,所以时间复杂度为O(log N)的算法基本上都很快,因此它也很有用。
3.复杂度为O(sqrt(N))的算法
一些算法的时间复杂度是O(sqrt(N)) (sqrt是平方根函数),但是它们并不很常见,并且本书中一个也没提到。这个函数增长得很慢但是比log(N)增长得快一点点。
4.复杂度为O(N)的算法
在规则1中描述的FindLargest复杂度是O(N)。请看该部分中它的复杂度为O(N)的解释。
函数N增长得比log(N)和sqrt(N)快但并不快太多,所以大多数复杂度是O(N)的算法在实践中表现都相当不错。
5.复杂度为O(N log N)的算法
假设一个算法遍历其输入中的所有元素,然后在每一个循环中,对那个元素执行了某种复杂度为O(log N)的计算。在这种情况下,这个算法的复杂度是O(N×log N)或O(N log N)。
另外,一个算法执行某种复杂度为O(log N)的操作,在这之中的每一步,对这个输入中的每一个元素都执行操作。
例如,假设像前文一样建立了一棵有N个元素的排序树。同时有一个包含N个值的数组。并且想知道数组中的哪一个值是在这棵树中。
一个方法是遍历这个数组中的值。对于每一个值,都用前文中描述的方法在树中搜索这个值。这个算法检查了N个元素,对于每个元素都执行了log(N)步操作,所以总时间复杂度是O(N log N)。
许多比较元素的排序算法其时间复杂度都是O(N log N)。实际上,可以证明任何通过比较元素的排序算法至少要O(N log N)步。所以至少在大O符号中,这是能做到的最好状况。即便如此,一些算法仍然比其他的算法快,这是因为在大O符号里,常量是被忽略的。
6.复杂度为O(N2)的算法
一个算法遍历所有输入,然后对于每一个输入都再次遍历每一个输入的操作时间复杂度就是O(N2)。例如,规则4中描述的ContainsDuplicates算法的时间复杂度是O(N2)。请看该部分对这个算法的描述与分析。
N的其他次幂,比如O(N3)和O(N4),都可能出现,但明显的比O(N2)慢。如果一个算法的时间复杂度包含多项式,包括N、O(N2)、O(N4)、O(N6)甚至是O(N4000),它的时间复杂度就是多项式时间复杂度。
多项式时间复杂度是重要的,因为在某种意义上,这些问题仍然能够被解决。下面将要描述的指数和阶乘函数增长得特别快,因此类似于指数函数和阶乘函数的算法在实际中只能解决有少量输入值的问题。
- 复杂度为O(2N)的算法
像2N这样的指数函数增长极快,所以只对小问题有实际意义。一般时间复杂度是指数级的算法都要选取最优的输入。
例如,考虑背包问题:给出一系列有价值和重量的物品,同时也有一个可以容纳一定重量的背包,可以选几个重的物品放在背包里,或者往里面放许多轻的物品。问题是如何能使背包装的物品价值之和最大。
这可能看起来是一个简单的问题。但是已知的寻找最佳方案的算法基本要求检验每个可能的组合。
下面看看一共有多少种可能的组合。请注意每一个物品可以放进背包也可以不放进背包,所以每个物品有两种可能。如果把这些数字乘起来,那么会得到2×2×…×2=2N个可能的选择。
有时不需要尝试每个可能的组合。例如,如果第一个物品就把背包完全填满了,就不需要把第一件物品和任何其他物品的组合包括在选择的物品内。然而,一般来说,不能排除足够多的可能性来缩小搜索的范围。
对于时间复杂度是指数函数的问题,经常需要使用启发式算法。它一般能产生不错的结果,但不能保证产生最佳结果。
8.复杂度为O(N!)的算法
阶乘函数写作N!,对于大于0的整数,定义为N!=1×2×3×…×N。这个函数增长得非常快,甚至比指数函数2N还快。时间复杂度是阶乘级的经典算法是寻找最佳的输入安排。
例如,在旅行商问题(Traveling Salesman Problem,TSP)中,输入是一份城市列表。目标是寻找一条恰好参观每个城市一次然后回到出发点、并且走过总路程最小的路线。
当城市很少时,这个问题并不难处理。但城市很多时,问题就变得有挑战性了。最显而易见的方法是尝试每个可能的安排。遵循着阶乘算法,在第一个城市有N种可能的选择。在做出选择后,接下来有N-1个城市可以访问。然后有N-2种可能的第三个城市,以此类推。所以安排的总数是N×(N-1)×(N-2)×…×1=N!。
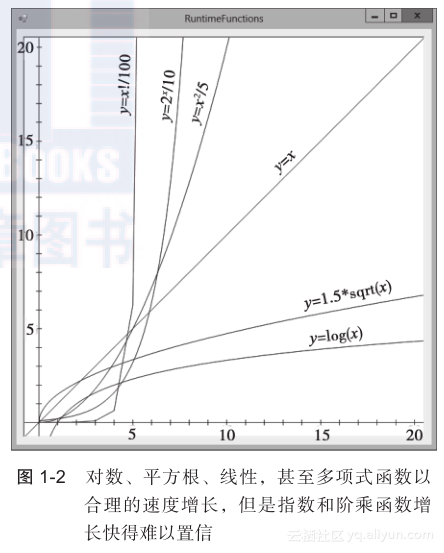
1.4.3 可视化函数
表1-1展示了一些前面描述的时间复杂度函数的值以便让读者了解这些函数增长得多么快。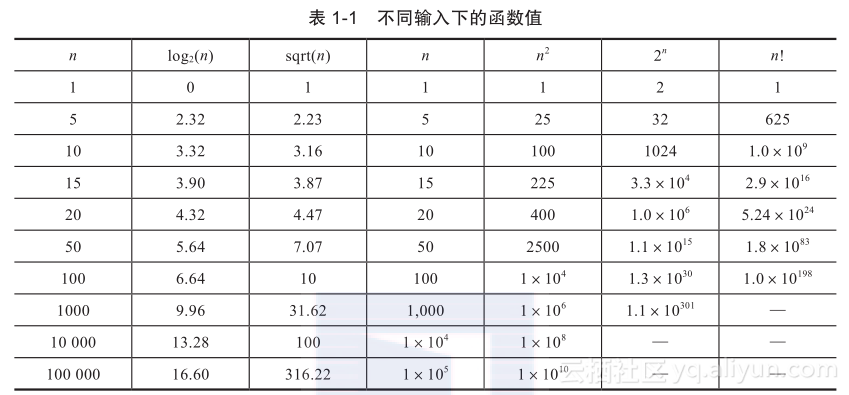
图1-2展示了这些函数的图像。有些函数的图像已经被缩放了,以便更好地适应这幅图。但是能轻易看出当x增大时哪个函数增长得更快。即使除以100也不能使阶乘函数在这个图上待很长时间。