阿里云开发者社区

大家在互动

大家在关注
综合
最新
有奖励
免费用
让你的文档从静态展示到一键部署可操作验证
通过函数计算的能力让阿里云的文档从静态展示升级为动态可操作验证,用户在文档中单击一键部署可快速完成代码的部署及测试。这一改变已在函数计算的活动沙龙中得到用户的认可。
一键生成视频!用 PAI-EAS 部署 AI 视频生成模型 SVD 工作流
本教程将带领大家免费领取阿里云PAI-EAS的免费试用资源,并且带领大家在 ComfyUI 环境下使用 SVD的模型,根据任何图片生成一个小短视频。
倚天使用|YODA倚天应用迁移神器,让跨架构应用迁移变得简单高效
YODA(Yitian Optimal Development Assistant,倚天应用迁移工具)旨在帮助用户更加高效、便捷地实现跨平台、跨结构下的应用迁移,大幅度缩短客户在新平台上端到端性能验
Paimon 与 Spark 的集成(二):查询优化
通过一系列优化,我们将 Paimon x Spark 在 TpcDS 上的性能提高了37+%,已基本和 Parquet x Spark 持平,本文对其中的关键优化点进行了详细介绍。
ECS实例选型最佳实践
本课程主要讲解在客户明确自身业务功能、性能、稳定性需求,以及成本成本约束后去了解各规格族/规格特性,匹配自身需求选择所需服务器类型。实例规格选型最佳实践,就是为了帮助用户结合自身业务需求中性能、价格、
创建to do list应用教程
阿里云讲师手把手带你部署to do list,本实验支持使用 个人账号资源 或 领取免费试用额度 进行操作,建议优先选用通过已领取的云工开物高校计划学生300元优惠券购买个人账号资源的方案,如您具备免
加载ModelScope模型以后,为什么调用,model.chat()会提示错误?
加载ModelScope模型以后为什么调用model.chat()会提示错误AttributeError: Qwen2ForCausalLM object has no attribute chat
阿里云百炼大模型产品实践
PAI-EAS 一键启动ComfyUI!SVD 图片一键生成视频 stable video diffusion 教程 SVD工作流
PAI-EAS 一键启动ComfyUI!SVD 图片一键生成视频 stable video diffusion 教程 SVD工作流

阿里云产品手册2024版
阿里云作为数字经济的重要建设者,不断加深硬核科技实力,通过自身能力助力客户实现高质量发展,共创数字新世界。阿里云产品手册 2024 版含产品大图、关于阿里云、引言、安全合规等内容,覆盖人工智能与机器学

conda数据源在昨天失效返回404,当前依赖的包无法安装和使用
问题描述conda数据源在失效返回404当前依赖的包无法安装和使用失效的镜像通道地址conda-forge: http://mirrors.aliyun.com/anaconda/cloud
Doodle Jump — 使用Flutter&Flame开发游戏真不错!
用Flutter&Flame开发游戏是一种什么体验?最近网上冲浪的时候,我偶然发现了一个国外的游戏网站,类似于国内的4399。在浏览时,我遇到了一款经典的小游戏:Doodle Jump...
更高效准确的数据库内部任务调度实践,阿里云数据库SelectDB 内核 Apache Doris 内置 Job Scheduler 的实现与应用
Apache Doris 2.1 引入了内置的 Job Scheduler,旨在解决依赖外部调度系统的问题,提供秒级精确的定时任务管理。
访问控制(RAM)|云上安全使用AccessKey的最佳实践
集中管控AK/SK的生命周期,可以极大降低AK/SK管理和使用成本,同时通过加密和轮转的方式,保证AK/SK的安全使用,本次分享为您介绍产品原理,以及具体的使用步骤。
All in One:Prometheus 多实例数据统一管理最佳实践
当管理多个Prometheus实例时,阿里云Prometheus托管版相比社区版提供了更可靠的数据采集和便捷的管理。本文比较了全局聚合实例与数据投递方案,两者在不同场景下各有优劣。
云效流水线智能排查功能实测:AI赋能DevOps,精准定位与高效修复实战评测
云效持续集成流水线Flow是阿里云提供的企业级CICD工具,免费且注册即用。它具备高可用性、免运维、深度集成阿里云服务、多样化发布策略及丰富的企业级特性。产品亮点包括智能排查功能,能快速定位问题,提高
【活动推荐】Alibaba Cloud Linux实践操作学习赛,有电子证书及丰厚奖品!
参与开放原子基金会的[龙蜥社区Alibaba Cloud Linux实践操作学习赛](https://competition.atomgit.com/competitionInfo),获取电子证书。报
日志服务 HarmonyOS NEXT 日志采集最佳实践
鸿蒙操作系统(HarmonyOS)上的日志服务(SLS)SDK 提供了针对 IoT、移动端到服务端的全场景日志采集、处理和分析能力,旨在满足万物互联时代下应用的多元化设备接入、高效协同和安全可靠运行的
Higress 基于自定义插件访问 Redis
本文介绍了Higress,一个支持基于WebAssembly (WASM) 的边缘计算网关,它允许用户使用Go、C++或Rust编写插件来扩展其功能。文章特别讨论了如何利用Redis插件实现限流、缓存
第十三期乘风伯乐奖--寻找百位乘风者伯乐,邀请新博主入驻即可获奖
乘风伯乐奖,面向阿里云开发者社区已入驻乘风者计划的博主(技术/星级/专家),邀请用户入驻乘风者计划即可获得乘风者定制周边等实物奖励。本期面向阿里云开发者社区寻找100位乘风伯乐,邀请人数月度TOP 1
号外号外!ClickHouse企业版正式商业化啦!
阿里云将于2024年4月23日14:00举办《ClickHouse企业版商业化发布会》直播,探讨阿里云ClickHouse企业版的架构、功能与优势,以及未来一年的产品规划。直播还将分享ClickHou

开源开发者沙龙北京站 | 微服务安全零信任架构
讲师/嘉宾简介 刘军(陆龟)|Apache Member 江河清(远云)|Apache Dubbo PMC 孙玉梅(玉梅)|阿里云技术专家 季敏(清铭)|Higress Maintainer 丁双喜(

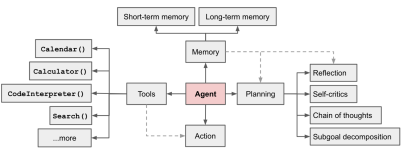
智能体(Agent)平台介绍
2023年11月9日,比尔盖茨先生发布了《人工智能即将彻底改变你使用计算机的方式》文章,详尽阐明了Agent(智能体)这个新一代智能应用的技术理念。在个人助理、卫生保健、教育、生产率、娱乐购物、科技等
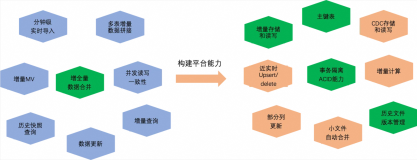
MaxCompute 近实时增全量处理一体化新架构和使用场景介绍
本文主要介绍基于 MaxCompute 的离线近实时一体化新架构如何来支持这些综合的业务场景,提供近实时增全量一体的数据存储和计算(Transaction Table2.0)解决方案。
PolarDB +AnalyticDB Zero-ETL :免费同步数据到ADB,享受数据流通新体验
Zero-ETL是阿里云瑶池数据库提供的服务,旨在简化传统ETL流程的复杂性和成本,提高数据实时性。降低数据同步成本,允许用户快速在AnalyticDB中对PolarDB数据进行分析,降低了30%的数
Flink CDC在阿里云DataWorks数据集成应用实践
本文整理自阿里云 DataWorks 数据集成团队的高级技术专家 王明亚(云时)老师在 Flink Forward Asia 2023 中数据集成专场的分享。

构建高效自动化运维系统:基于容器技术的策略与实践
【4月更文挑战第19天】随着云计算和微服务架构的兴起,传统的运维模式正逐渐向自动化、智能化转型。本文将探讨如何利用容器技术构建一个高效、可靠的自动化运维系统,涵盖系统设计原则、关键技术选型以及实践经验