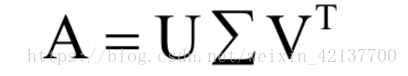奇异值分解
(singular value decomposition)是
线性代数
中一种重要的
矩阵分解
,在
信号处理
、
统计学
等领域有重要应用。奇异值分解在某些方面与
对称矩阵
或
Hermitian矩阵
基于
特征向量
的
对角化
类似。然而这两种矩阵分解尽管有其相关性,但还是有明显的不同。对称阵特征向量分解的基础是
谱分析
,而奇异值分解则是谱分析理论在任意矩阵上的推广。
A为m×n矩阵,rank(A)= r, 可以分解为:A=UDV',其中U'U=V'V=I。在R中可以用函数svd()进行奇异值分解,其中D需要使用diag()转换为矩阵.
例如 :
验证 :
> A=matrix(1:18,3,6)
> A
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 4 7 10 13 16
[2,] 2 5 8 11 14 17
[3,] 3 6 9 12 15 18
> rank(A)
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
> svd(A)
$d
[1] 4.589453e+01 1.640705e+00 1.366522e-15
$u
[,1] [,2] [,3]
[1,] -0.5290354 0.74394551 0.4082483
[2,] -0.5760715 0.03840487 -0.8164966
[3,] -0.6231077 -0.66713577 0.4082483
$v
[,1] [,2] [,3]
[1,] -0.07736219 -0.71960032 -0.4076688
[2,] -0.19033085 -0.50893247 0.5745647
[3,] -0.30329950 -0.29826463 -0.0280114
[4,] -0.41626816 -0.08759679 0.2226621
[5,] -0.52923682 0.12307105 -0.6212052
[6,] -0.64220548 0.33373889 0.2596585验证 :
A=UDV',
注意$d是向量, 需要转换为矩阵
diag(svd(A)$d).
验证 :
> svd(A)$u %*% diag(svd(A)$d) %*% t(svd(A)$v)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 4 7 10 13 16
[2,] 2 5 8 11 14 17
[3,] 3 6 9 12 15 18验证 :
U'U=V'V=I
> t(svd(A)$u) %*% svd(A)$u
[,1] [,2] [,3]
[1,] 1.000000e+00 3.330669e-16 1.665335e-16
[2,] 3.330669e-16 1.000000e+00 5.551115e-17
[3,] 1.665335e-16 5.551115e-17 1.000000e+00
> t(svd(A)$v) %*% svd(A)$v
[,1] [,2] [,3]
[1,] 1.000000e+00 2.775558e-17 2.775558e-17
[2,] 2.775558e-17 1.000000e+00 -2.081668e-16
[3,] 2.775558e-17 -2.081668e-16 1.000000e+00
> round(t(svd(A)$v) %*% svd(A)$v)
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
> round(t(svd(A)$u) %*% svd(A)$u)
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
参考]